圆柱滚子轴承滚道圆度误差对旋转精度的影响
宋飞,李济顺,2,刘永刚,2
(1.河南科技大学 机电工程学院,河南 洛阳 471003;2.河南省机械设计及传动系统重点实验室,河南 洛阳 471003)
滚动轴承的旋转精度是表征其质量的一个主要指标,既影响轴承运转时的工作性能,也反映了轴承的制造精度[1-2]。为了提高轴承的旋转精度,轴承行业从控制轴承零件工作表面的几何误差着手,提升零件的制造精度,并取得了显著的成果[3-5]。对于圆柱滚子轴承,其零件的圆度和圆柱度等可以采用3点法误差分离技术和提纯技术进行精密测量和重构[6-9]。利用GPS标准的数字化计量方法,可以对圆度、圆柱度的误差进行评定[10-12]。圆柱滚子轴承的内圈、外圈、滚子和保持架等都有其自身的精度,各自精度的差异和运动副间隙及其相互作用必定影响成品轴承的旋转精度,然而在这方面的研究较少,尤其关于轴承零件的几何精度与旋转精度之间的关系方面更是鲜见报道。下文以圆柱滚子轴承为研究对象,在轴承零件形状误差研究的基础上,分析滚道圆度误差对旋转精度的影响,为建立圆柱滚子轴承旋转精度的预测和评价体系,设计和开发高精度圆柱滚子轴承提供理论支持。
1 数学模型的建立
1.1 基本假设
(1)滚子、套圈在轴承径向平面内做平面运动,内圈有3个自由度,分别为径向平面内两垂直方向的平移和绕自身轴线的转动。
(2)外圈固定,滚子为纯滚动,滚子与外圈滚道完全接触,内圈以恒定的角速度旋转。
(3)不考虑弹流润滑条件,不计其他形状误差(外圈滚道圆度误差、滚子的圆柱度误差等)对旋转精度的影响。
1.2 内圈滚道圆度误差简化
内圈圆度误差可以表示为Fourier级数形式
(1)
式中:θ为内圈滚道的角度变量;N为圆度误差谐波分量的最高阶数;An和Bn分别为内圈滚道圆度误差第n阶谐波分量的余弦项和正弦项系数。
为简化计算,内圈滚道曲线形状可以用标准圆和Fourier级数的谐波分量表示,如图1所示,则滚道曲线在直角坐标系下的参数方程为

图1 内滚道圆度误差简化
(2)
式中:F为内圈滚道直径;R(θ)为Fourier级数的谐波分量。
1.3 建立坐标系
为了能方便地描述轴承及其零件的运动,将圆柱滚子轴承放在设定的坐标系中进行分析。根据圆柱滚子轴承的特点,建立整体坐标系(x,y,z)和内圈的局部坐标系(xr,yr,zr),在整体坐标系中,z轴沿轴承轴线方向,x-y面与轴承滚道的径向平面重合,如图2所示。
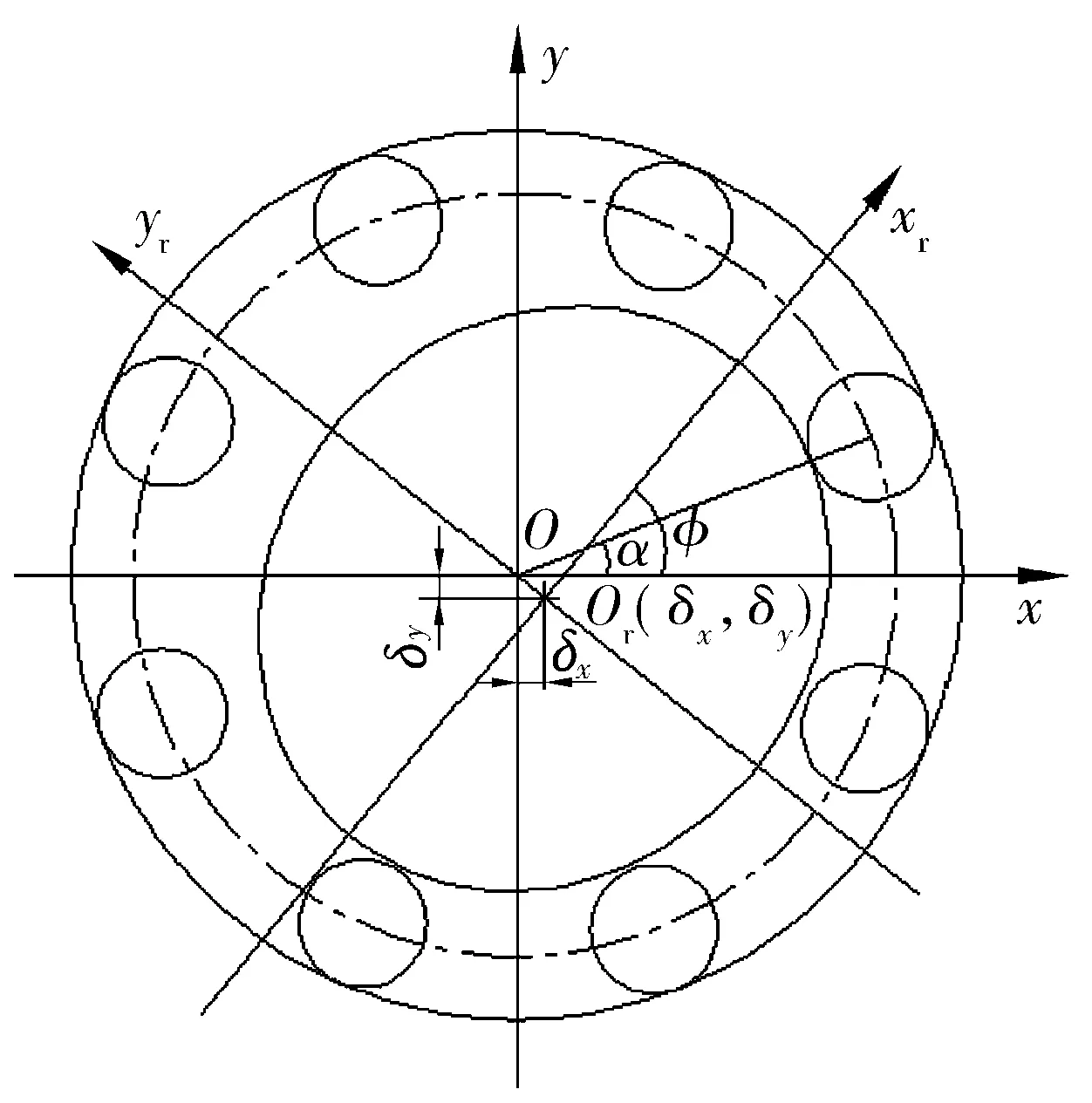
图2 坐标系系统
坐标变换的一般形式为
(3)
式中:φ为内圈转过的角度;δx,δy为内圈圆心相对于轴心的变化量。
1.4 轴承各零件的几何关系
根据运动几何关系得
(4)
式中:α为滚子绕轴线转过的角度;Dpw为滚子组节圆直径;Dw为滚子直径。
第i(i=1,2,…,Z)个滚子圆心的坐标为
(5)
滚子圆心到内圈滚道曲线的距离为
(6)
2 数值仿真与模拟
通过建立的数学模型,对圆柱滚子轴承的运动状态进行数值仿真与模拟,程序流程图如图3所示,实现的步骤如下。

图3 程序流程图
(1)设定相关参数。根据轴承设计手册查得圆柱滚子轴承零件的参数值,比如内径、外径和径向游隙等。在整体坐标系下,设定内圈的转动步长为h=2π/n(n为正整数),则转过的角度为φj=jh(j=1,2,…,n),取Fourier级数的谐波分量为R(θ),滚道的圆度误差用Fourier级数的谐波分量表示。根据 (2)~(5) 式和已知的参数值,可以得到滚道曲线在整体坐标系下的参数方程及滚子的圆心坐标值。
(2)运动仿真。在不考虑载荷作用的情况下,外圈固定,滚子为纯滚动,内圈按设定的步长转动,内圈每转动一个步长,沿坐标轴方向平移内圈,平移步长为Δx,Δy,旋转中心相对于整体坐标系原点的变化量为δx,δy,分别计算每个滚子圆心到内圈滚道曲线的距离,进而判断滚道与滚子的接触情况。
(3)判断有效接触及滚子接触数。若滚子圆心到滚道曲线的距离与滚子的半径之差在允许的误差范围内(如圆度误差值的1%),可认为是有效接触,由力学平衡条件可知,滚子和套圈至少有两点接触时才能处于平衡状态,在内圈的平移量内,分别记下滚道与滚子的接触数m≥2的中心坐标值,在内圈转动的一个步长内,输出有效接触数最大值及对应的旋转中心坐标值(δx,δy)。内圈转动一周即可得到一系列的坐标值(δx1,δy1),(δx2,δy2),…,这些中心坐标点所在的区域即为内圈旋转中心的取值范围。
3 计算示例

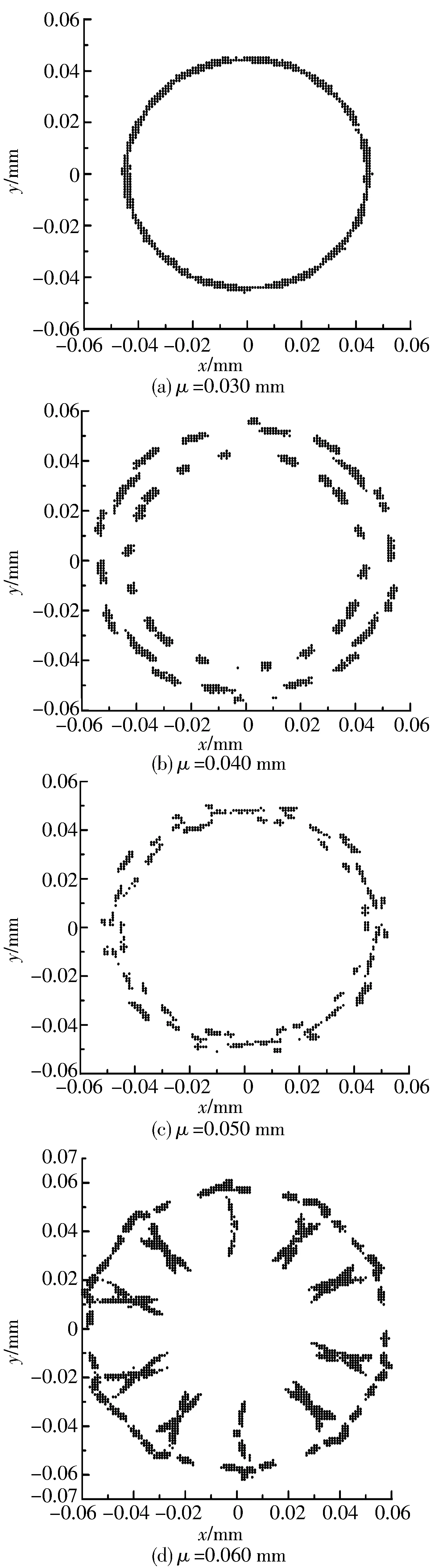
图4 内圈滚道不同的圆度误差对应的旋转中心坐标

表1 轴承的计算参数
由不同圆度误差的旋转中心分布特点可知,随着圆度误差的增大,中心坐标点分布扩散,内圈旋转中心的振动幅值增大,在转动过程中轴承零件的形状误差越大,产生的振动特性越明显,计算结果与实际情况比较吻合。对不同圆度误差对应的内圈旋转中心的最大幅值进行曲线拟合,从图5可以看出,随着内圈滚道圆度误差的增大,内圈旋转中心的幅值增大,旋转精度降低,圆度误差越大,旋转中心幅值上升趋势越平缓。由此可以推断,在径向游隙的范围内,旋转中心的最大幅值会随滚道圆度误差的增大而达到某一极限值。

图5 不同圆度误差对应的旋转中心幅值
4 结论
(1)轴承零件的圆度误差是影响其旋转精度的一个重要因素,根据不同圆度误差的旋转中心分布特点及规律,可以有效地预测轴承的旋转精度。
(2)滚道的圆度误差越大,旋转中心的幅值变化越明显,在径向游隙的范围内,旋转中心的最大幅值随滚道圆度误差的增大将达到某一极限值。

