稠密栅元不同子通道内湍流流动的RANS和URANS模拟
于意奇,顾汉洋,杨燕华,程 旭
(上海交通大学 核科学与工程系,上海 200240)
稠密栅元的燃料组件广泛应用于先进的反应堆设计。因稠密的栅元结构将减少水铀比从而硬化了中子能谱,这将提高转换比并增加燃料利用率[1-3]。
最早的棒束内的湍流流动实验研究开始于20世纪60年代。近年来,随着实验测量手段的发展,越来越多的实验研究开始关注于棒束内的湍流流动[4-9]。
实验研究表明:棒束内的湍流流动和圆管内的完全不同,在棒束间隙区有很强的交混。这一现象曾被归结于二次流,不过,最近的实验研究表明这并不是影响棒束间强交混的主要因素。棒束间隙区的准周期流动振动才是影响子通道间能量质量交换的最主要因素。这种流动振动和子通道的几何构造与雷诺数密切相关,当雷诺数低于一定的临界值时,这种振动便消失[10]。实验发现,壁面通道中,在1.015≤W/D≤1.250(W 为棒最远端距壁面的距离,D为棒径)的范围内,流动振动的频率随间隙的减小而减小[11]。尽管对这一流动振动现象还未完全了解,但学术界普遍认为这是由于流动的不稳定造成的。
如今,RANS、LES、URANS和 DNS方法均被应用于模拟棒束内的湍流流动[12-16]。研究表明:采用各向同性的湍流模型的稳态模拟(RANS)无法再现棒束流动的强各向异性的特点。尽管采用各向异性的湍流模型的稳态模拟可模拟出湍流驱动的二次流现象,但在P/D(P为两棒之间的中心距离)较小的稠密栅元子通道内,二次流不是影响流动的主要因素。所以,在这些子通道中,模拟的结果往往与实验有一定的差距。尽管数值模拟粗略高估了振动的波长,URANS方法对稠密栅元棒束间隙的流动振动有较好的模拟结果。
在这些方法中,DNS方法是最理想的一种,因为对于整体的流动振动现象还不是十分了解。LES方法几乎可得到和DNS相同的结果。但由于LES和DNS的计算代价太大,URANS是目前比较实际的一种数值模拟方法。
1 数值方式
在本研究中,将选用不同P/D和通道形状的子通道实验作为参考。详细的实验参数和数值模拟信息列于表1[4,17-18]。实验截面图示于图1。

表1 本工作的实验和数值参数Table 1 Experimental and numerical parameters
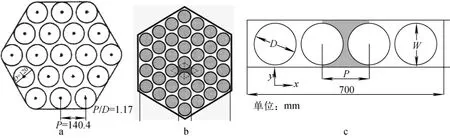
图1 实验截面图Fig.1 Set-up cross-section
1.1 RANS模拟
由于子通道的对称性,选用1/6和1/4子通道作为RANS模拟的计算域,如图2所示。棒、通道和表面采用非滑移的边界条件,进口采用均流的边界条件,出口设置定压的边界条件,其余为对称的边界条件。通过网格敏感性分析,分别得到25万的中心子通道网格和50万的壁面子通道网格。采用涡粘性和雷诺应力模型来评估它们对于稠密栅元内湍流模拟的适用性。涡粘性模型包括k-ε模型和SST模型,雷诺应力模型包括ORS、SSG和BSL模型。所有模型均采用壁面函数模拟近壁面的流动。所有近壁面网格保持y+=1。

图2 RANS的计算域Fig.2 Computational domain for RANS
1.2 URANS模拟
URANS计算域包括两个由间隙连接的子通道(图3)。整个计算包括3组周期性边界条件和非滑移的壁面边界条件。进出口的周期性边界条件固定质量流速,计算长度为0.6m(4倍于实验测量的平均波长λ)。

图3 URANS的计算域Fig.3 Computational domain for URANS
网格总数为60万,时间步长满足:Δt≪1/f,f为最小振动频率,Δt选为10-4s。几乎所有应用于RANS模拟的湍流模型均被应用于URANS计算。另外,专为瞬态模拟设计的SAS湍流模型也将应用于URANS计算。
2 结果和讨论
本工作对所有工况均进行了RANS模拟,对P/D=1.06的三角形排列的中心通道和4棒束平行排列的子通道进行了URANS计算,并将主流速度、壁面剪应力、湍动能和壁面温度等参数与文献[4]的实验结果进行比较。
2.1 主流速度
对于P/D为=1.17的三角形排列子通道,RANS模拟计算结果示于图4。图中,y为径向上与壁面距离,v为主流速度。棒束内的二次流虽尺度很小,但它将影响子通道内的湍流分布。雷诺应力模型将湍流的各向异性考虑在内,所以,雷诺应力湍流模型(BSL,ORS,SSG)较涡粘性湍流模型(k-ε,SST)得到的速度分布更接近实验测量结果。由图3b可见,SSG湍流模型的模拟计算结果与实验测量结果吻合良好。
P/D=1.06的三角形排列稠密栅子通道内的速度分布示于图5。图中,Wb为主流速度,ymax为径向上速度最大值与壁面的距离。在棒束间隙区(φ=30°),RANS和 URANS的计算结果有很大差异,其原因在于棒束间隙区存在强烈的速度振动。在URANS的计算结果中,各向异性的SSG湍流模型给出了对实验更好的预测。4棒平行排列稠密栅元子通道的速度分布示于图6。由图6同样发现,在棒束间隙区,URANS的结果较RANS有很大改进。

图4 P/D=1.17的三角形排列子通道主流速度分布Fig.4 Velocity distributions in triangular array with P/D=1.17

图5 P/D=1.06的三角形排列稠密栅子通道内速度分布Fig.5 Velocity distributions in triangular array with P/D=1.06

图6 P/D=1.12、W/D=1.06的4棒束平行排列子通道速度分布Fig.6 Velocity distributions in 4rod parallel array with P/D=1.12,W/D=1.06
2.2 壁面剪应力
图7示出P/D=1.17的三角形排列子通道内的壁面剪应力tau的分布。图中,taum为壁面平均剪应力。图7a显示,雷诺应力湍流模型(SSG、BSL、ORS)的模拟结果更为平坦,较涡粘性湍流模型(k-ε、SST)也更接近实验结果。这是由于雷诺应力湍流模型对二次流的模拟均化了壁面剪应力的分布。图7b示出了雷诺数更高的情况,模拟结果同样证实了上述结论。
图8示出P/D=1.06的三角形排列子通道内的壁面剪应力分布。由图8可见,在URANS计算方式下,即便采用各向同性的k-ε湍流模型,得到的结果也比在RANS计算方式下采用SSG湍流模型得到的结果更接近实验测量结果。这也证明了在P/D较小的稠密栅元子通道中,二次流不再是主导的影响因素。

图7 P/D=1.17的三角形排列子通道内的壁面剪应力分布Fig.7 Wall shear stress distributions in triangular array with P/D=1.17

图8 P/D=1.06的三角形排列子通道内壁面剪应力分布Fig.8 Wall shear stress distributions in triangular array with P/D=1.06
同样,在URANS计算方式下,雷诺应力湍流模型(SSG、ORS)的模拟结果较涡粘性湍流模型(k-ε、SST)更接近实验测量结果。
URANS同样得到更为均化的壁面通道壁面剪应力的分布(图9),并与实验吻和良好。在RANS计算中,只有各向异性的湍流模型可模拟出二次流。而在URANS计算中,流动的对称性被打破,在短时间平均下无法观察到二次流,但在足够长的时间下采用雷诺平均,即使采用各向同性的湍流模型也能重现二次流。
2.3 湍动能
稠密栅间隙区的流动振动是一种相干结构,在比较湍动能时,有必要把这种流动振动贡献考虑在内。通常,相对湍动能的定义如下:

式中:u、v、w分别为轴向速度波动、径向速度波动和周向速度波动;uτ为壁面剪应力;k+nc为湍动能的非相干部分。由速度振动引起的湍动能称为湍动能的相干部分k+c,其定义如下:

总湍动能为两部分之和:

图10示出三角形排列和4棒束平行排列的子通道在不同周向角度上的湍动能分布。由图10可见,URANS的计算精确性高于RANS。专门为非稳态计算设计的SAS湍流模型较其他湍流模型有着更高的模拟精度。

图9 P/D=1.12、W/D=1.06的4棒束平行排列子通道壁面剪应力分布Fig.9 Wall shear stress distributions in 4rod parallel array with P/D=1.12,W/D=1.06

图10 稠密栅元子通道湍动能分布Fig.10 Turbulent intensity distributions in tight lattice
2.4 壁面温度
图11示出P/D=1.06的三角形排列子通道壁面温度分布,温度通过平均温度来进行无量纲化处理。由图11可见,URANS的模拟结果更为均化并与实验测量结果吻合良好。因此,稠密栅元内的流动振动均化了壁面温度,对于反应堆堆芯的工业设计是有利的。

图11 P/D=1.06的三角形排列子通道壁面温度分布Fig.11 Wall temperature distributions in triangular array with P/D=1.06
2.5 流动振动
稠密栅元子通道内的流动振动缓慢发展,最后发展为稳定的波动(波幅达到常值或准常值)。图12示出三角形排列子通道窄缝区的横向速度随时间的变化和三维振动快照。振动幅度为2m/s,与文献[4]的实验测量结果相近。然而,计算所得振动波长比实验测量结果大。
总体而言,URANS仍无法模拟稠密栅元内相干结构的所有特性,但对于正确预测主流速度、壁面剪应力和壁面温度等工业关心的统计变量十分实用。
3 结论
本工作对典型的子通道(中心通道和壁面通道)进行URANS和RANS计算。计算结果表明,在较宽的稠密栅元通道(P/D=1.17)内,采用SSG湍流模型的RANS计算能很好地再现实验结果。对于P/D较小(P/D<1.1)的稠密栅元子通道,窄缝区内大尺度的流动振动将显著影响子通道的湍流流动。URANS模拟虽无法再现稠密栅元子通道内流动振动的所有动力特性,但可很好地预测子通道内的主流速度、壁面剪应力、湍动能分布。推荐采用SAS和SSG湍流模型进行URANS计算。

图12 P/D=1.06的三角形排列子通道窄缝区横向速度波动(a)和三维流动振动快照(b)Fig.12 Flow pulsation(a)and dimension snapshot of oscillation(b)in narrow gap in triangular array subchannel with P/D=1.06
[1]OLDEKOP W,BERGER H D,ZEGGEL W.General features of advanced pressurized water reactors with improved fuel utilization[J].Nuclear Technology,1982,59:212-227.
[2]UCHIKAWA S,OKUBO T,KUGO T,et al.Investigations on innovative water reactor for flexible fuel cycle(LFWR)[C]∥Proceedings of GLOBAL.Tsukuba,Japan:[s.n.],2005.
[3]CHENG X,LIU X J,YANG Y H.A mixed core for supercritical water-cooled reactors[J].Nuclear Engineering and Technology,2008,40(1):1-10.
[4]KRAUSS T,MEYER T.Experimental investigation of turbulent transport of momentum and energy in a heated rod bundle[J].Nuclear Engineering and Design,1998,180:185-206.
[5]TRUPP A C,AZAD R S.The structure of turbulent flow in triangular array rod bundles[J].Nuclear Engineering and Design,1975,32:47-84.
[6]TRIPPE G,WEINBERG D.Non-isotropic eddy viscosities in turbulent flow through rod bundles[M]∥Turbulent Forced Convection in Channels and Bundles:Vol.1.KAKAC S,SPALDING D B.Washington:Hemisphere Publishing Corporation,1979:505.
[7]SEALE W J.Turbulent diffusion of heat between connected flow passages[J].Nuclear Engineering and Design,1979,54:183-195.
[8]REHME K.Simple method of predicting friction factors of turbulent flow in non-circular channels[J].International Journal of Heat and Mass Transfer,1973,16:933-950.
[9]REHME K.The structure of turbulent flow through rod bundles[J].Nuclear Engineering and Design,1987,99:141-154.
[10]MEYER L,REHME K.Large-scale turbulence phenomena in compound rectangular channels[J].Experimental Thermal and Fluid Science,1994,8:286-304.
[11]BARATTO F,BAILEY S C C,TAVOULARIS S.Measurements of frequencies and spatial correlations of coherent structures in rod bundle flows[J].Nuclear Engineering and Design,2006,236:1 830-1 837.
[12]BAGLIETTO E,NINOKATA H.Turbulence models evaluation for heat transfer simulation in tight lattice fuel bundles[C]∥Proceedings of the 10th International Topical Meeting on Nuclear Reactor Thermal Hydraulics (NURETH-10).Seoul,Korea:[s.n.],2003.
[13]CHANG D,TAVOULARIS S.Unsteady numerical simulations of turbulence and coherent structures in axial flow near a narrow gap[J].ASME Journal of Fluids Engineering,2005,127(3):458-466.
[14]CHANG D,TAVOULARIS S.Numerical simulation of turbulent flow in a 37-rod bundle[J].Nuclear Engineering and Design,2007,237:575-590.
[15]MERZARI E,NINOKATA H,BAGLIETTO E.Large eddy simulation of the vortex street between rectangular channels[C]∥NTHAS 5.Jeju Island,Korea:[s.n.],2006.
[16]NINOKATA H,MERZARI E,KHAKIM A.Analysis of low Reynolds number turbulent flow phenomena in nuclear fuel pin subassemblies of tight lattice configuration[J].Nuclear Engineering and Design,2009,239(5):855-866.
[17]KRAUSS T.Experimentelle untersuchung des turbulenten wärme-und impulstransports in einem beheizten stabbündel [R].Germany:Karlsruhe University,1996.
[18]MANTLIK F,HEINA J,CHERVENKA J.Results of local measurements of hydraulic characteristic in triangular pin bundle,UJV-3778-R[R].Rzez,Czech Republic:[s.n.],1976.

