基于分块不变矩特征的瓷砖分类识别的研究*
卞玉丽,郑力新,晏来成,徐园园
(华侨大学 信息科学与工程学院,福建 厦门361021)
我国是瓷砖生产大国,生产企业众多。在一些中小企业中,由于生产条件、成本等因素的制约,往往多种花纹的瓷砖共用一条生产线,主要靠大人工将不同类别的瓷砖分开,劳动强度大,效率低下且出错率高。国内已展开与瓷砖相关的研究,如瓷砖的颜色分类、表面检测等,当前大部分的研究内容,不管是分类还是缺陷识别,都涉及当前瓷砖与模板库中的瓷砖进行比对匹配。参考文献[1]检测缺陷前根据瓷砖的边缘进行配准,然后再匹配,配准前利用Hough变换检测瓷砖的4个边缘,计算量大,且检测结果易受到噪声干扰。参考文献[2]在分类前假定生产线上瓷砖的摆放方式是固定的,这样固然可以省去配准的步骤,但是也会使实用性大打折扣,因为生产线瓷砖的摆放方式不可能是固定的。参考文献[3]利用遗传算法进行配准,配准后再用模板匹配识别,由于配准和匹配都比较耗时,因此实时性较差,很难应用于生产现场。在这种背景下,找到一种快速、与摆放位置无关或者关系较小的特征对于瓷砖的分类识别具有重要意义。本文首先通过形态学边缘检测算子检测瓷砖的花纹,然后将瓷砖分成4×4的子块,计算每个子块的Hu不变矩,选取其中第1个和第4个最稳定的两个矩作为本子块的特征,16个子块的特征全部被提取后,输入BP神经网络(Back Propagation Network)进行分类识别。
1 特征提取
1.1 边缘检测
对于分类识别问题,特征的选取具有极其重要的作用。对于瓷砖这样表面具有明显花纹的对象,选择花纹作为分类依据是非常自然的选择,且已有一些论文采用纹理特征,具体来说是采用灰度共生矩阵作为分类的依据。
图1中的瓷砖图片里充满着肉眼很难发现的细小的纹理,但是之所以称其为一类,不是由这些极小的细节决定的,而是由其宏观的由若干个方格组成的图案决定的。如果采用灰度共生矩阵,那些过小的细节被不太必要地考虑进去,这样不仅使得程序运行速度较慢,而且过多的冗余信息可能会影响分类的正确率。
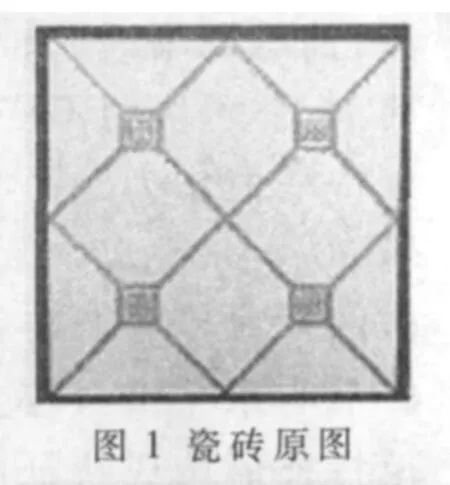

明显的花纹形状和走向是分类的主要依据,基于这一事实,本文首先通过边缘检测将花纹提取出来。图2是对图1 Canny边缘检测的结果。Canny等常见边缘检测算子归根结底是对图像进行求导得到的,而瓷砖的表面其实有些许细小的、无规律的纹理,这些肉眼都无法看清楚的纹理对分成不同类别的瓷砖没有太多价值(当然,如果待分类的瓷砖只有极小的纹理不同时则令当别论),且若处理不当还会产生负面影响。
形态学梯度的定义为:

形态学梯度是通过膨胀后的图像减去腐蚀后的图像得到的。膨胀和腐蚀都可以指定结构元素的形状和尺寸,较大尺寸的结构元素能够检测明显花纹,较小尺寸的结构元素则检测细小的花纹。本文采用圆形结构元素,尺寸为9×9。按照以下次序进行处理即可:RGB图像→灰度图像→图像中值滤波去除噪声→形态学边缘检测→二值化→腐蚀运算消除小的干扰点。图3是形态学方法检测的边缘图像,较好地反映了原图的花纹走向,可以作为分类的依据。

1.2 矩特征[4]
不变矩是图形的一种统计特征,它利用图像的灰度分布的各阶矩来描述图像灰度的分布特征,在模式识别、目标分类中得到了广泛的应用。
1.2.1 原点矩
二维原点矩的定义为:
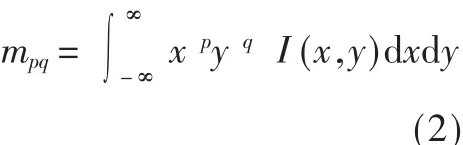
对于离散图像,通常近似为:
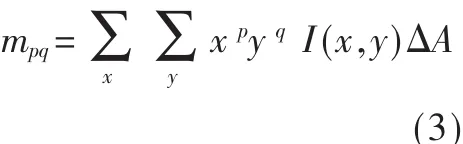
其中,ΔA表示像素的大小。
1.2.2 中心矩
然而,更多需求的是基本不变量,即希望得到的特征量与物体的位置、大小(即旋转)无关。中心矩具有位置无关性,其定义为:
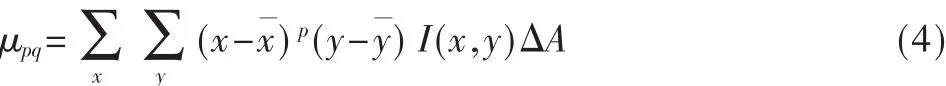
1.2.3 不变矩
中心矩具有平移不变性,即其仅对位置变换保持不变,而对旋转则不具有不变性。为了得到旋转和尺度不变性,需正规化中心矩,于是定义:
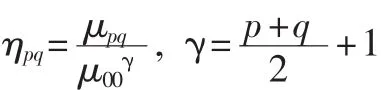
在此基础上可以计算出7个不变矩:
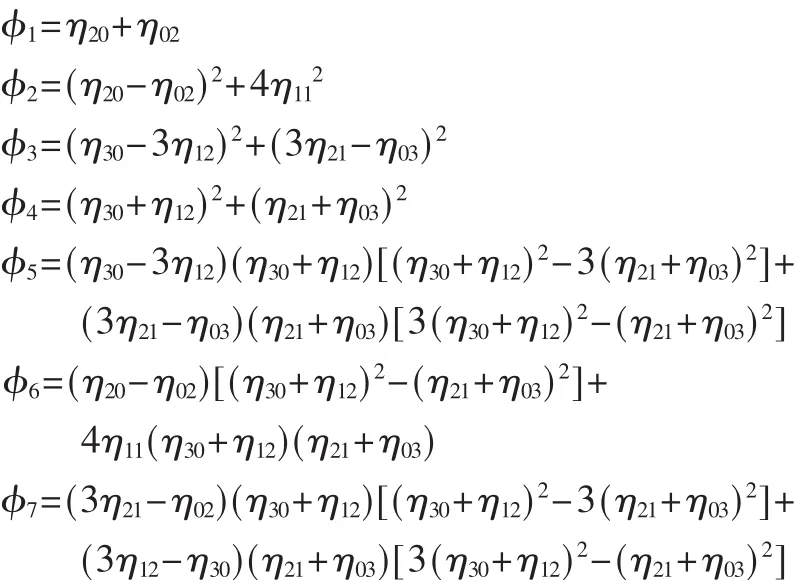
1.3 分块的矩特征提取
1.3.1 分块特征选择
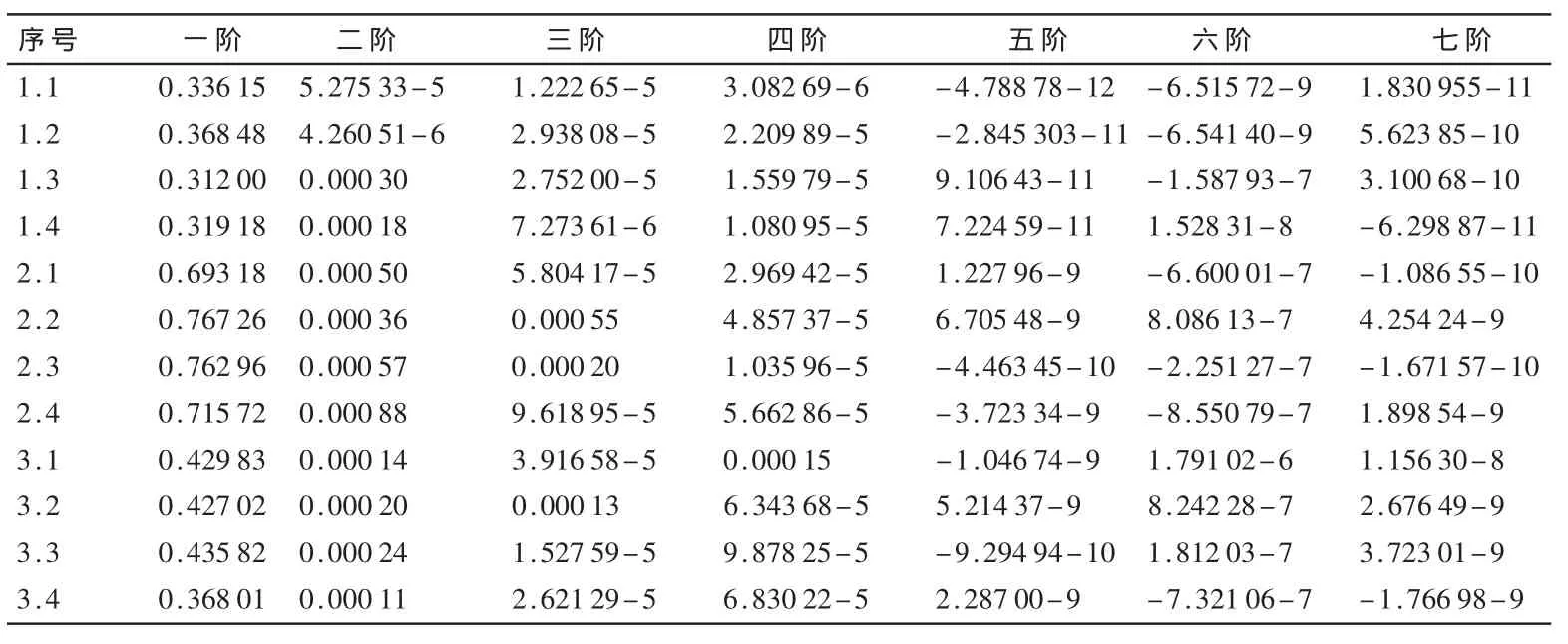
表1 3种类别12种瓷砖的7个不变矩数据
表1是3种类别12种瓷砖的7个不变矩数据。可以看出,同一类别的瓷砖的不变矩中有多个表现较为不稳定,第5、6、7个,即便是同一块瓷砖拍摄的多张照片之间也会有较大出入;但有些矩,比如第1、2、4个,则表现相对较为稳定。如果仅仅采用稳定的两个或者3个矩特征作为分类的依据,数量太少,势必会使分类精度下降,尤其当瓷砖之间的花纹差别不大时更为明显。同时,不变矩描述的是图像的整体特征,对局部信息的刻画较差,即便不存在部分不变矩不稳定的情况也是如此。在这种背景下,本文首先将瓷砖分成4×4个小块,然后计算每个小块的不变矩,从中选取两个较为稳定的,即整体共32个特征作为一个瓷砖的特征向量。这样既去掉了不稳定的高阶矩,同时,采取分块的思想后,瓷砖的每个子部分都有相对应的矩,虽然对于子部分而言矩仍是全局特征,但对于整体来说,矩则变成了局部特征,描述刻画对象的能力就更强了。
通过分析表1可以发现,前4个不变矩比较稳定,尤其是第1个、第2个及第4个距的数据在同类瓷砖之间比较接近,适合作为识别特征。本文选择第1个与第4个不变矩(为了叙述方便,文中将7个不变矩分别简称一阶矩、二阶矩等)作为每个子块的特征。
1.3.2 特征不变处理
不变矩本身与瓷砖的大小、摆放位置无关,具有较好的鲁棒性,但是由于进行了分块,这样矩就与位置相关了。瓷砖在生产线上的摆放应该是随机的,为了更具有一般性,本文假定瓷砖为关于圆心不对称的图形。
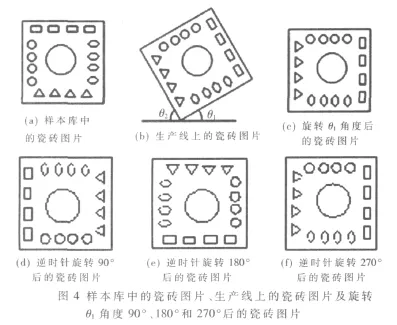
图4(a)是训练样本库中已知类别的某种瓷砖图片,而图4(b)是生产线上同类别的一个瓷砖图片。可以看出,要想正确判断出瓷砖的类别,必须将其旋转成图4(a)中的位置。但在分类之前根本无法判断它是属于哪种类别,更别说将其旋转成所谓的正确位置了。本文的思路是,对于某一待识别的瓷砖,首先找出其最小外接矩形,由于瓷砖基本都是方形的,因此,最小外接矩形4个边就是其4条边线。分别计算最小外接矩形的4条边与水平 线的 夹角,分 别为 θ1、θ2,找 出 它 们 中 较 小 的 那 个(如θ1),然后根据较小的角出现的位置,对应地将瓷砖顺时针或者逆时针旋转 θ1角度,图4(b)旋转之后变成了图4(c)。可以看出此时与图4(a)还是不同,但将图4(a)逆时针旋转 270°后即为图 4(f),就与图 4(c)一样了。图 4(d)、图 4(e)、图 4(f)分 别 是 将 图 4(a)逆 时 针 旋 转 90°、180°、270°后形成的3张图片。那么同类别待识别的瓷砖,在将其按较小角θ1旋转至水平位置后,总是可以与图4(a)、图 4(d)、图 4(e)和图 4(f)这4幅图片中的一个相同。
综上所述,解决分块后位置相关性问题可以总结为:训练网络时,首先将每个样本旋转至水平位置,提取其16个子块的不变距作为特征值 (共32个),再将32个特征值作为一个特征向量。分别将样本图片逆时针旋转 90°、180°、270°后再分块提取特征, 这样一个训练瓷砖图片对应4个特征向量。分类识别时,将待识别的瓷砖沿与水平线最小夹角旋转后,提取16个子块的不变矩特征值构成特征向量,然后将特征向量作为识别网络的输入。这样不管待识别的瓷砖位置如何,都能被正确地分类识别。
2 分类
2.1 网络结构[6-7]
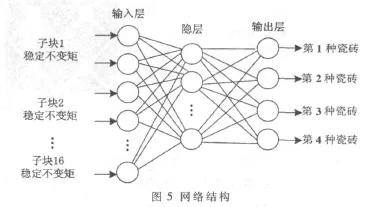
BP神经网络是应用最多的一种神经网络,它把网络的学习过程分为正向传播和反向传播两种交替过程,输入的信号经输入层、隐含层的神经元最终向前传播到输出层给出结果。如果在输出层得不到期望的结果,则转入逆向传播过程,期望值与实际值之间的误差反向传播回去。通过修改各层神经元权值使得误差减小,然后再转入正向过程,如此反复,直至误差满足要求为止。本文采用的BP网络具有三层,输入层有32个点,输出4个神经元。某个神经元输出为1代表结果为本类瓷砖,如0010代表结果为第2类瓷。由于S函数的特点,输出实际上很难是绝对的1或0,在本文中,输出0.9代表1,0.1代表0。隐层神经元的个数具有一定的随意性,可以根据实际情况作相应的调整,本文选8个隐层神经元。整体的网络结构如图5所示。
2.2 避免局部极小值[6]
BP算法在解空间中寻找能够将误差最小化的网络权值,由于S函数为非线性函数,误差曲面可能包含多个局部极小值,在搜索时有可能陷入到局部极小值中去,这是要尽量避免的。前文所述将初始值随机取值也是避免局部极小值的一种手段,除此之外,本文还采用以下措施。
(1)增加动量因子。带有附加动量因子的权值调整公式为:
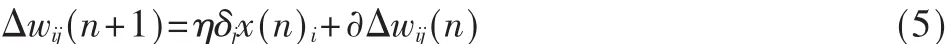
其中,∂为动量因子,一般取0.01~0.95。
增加动量因子后,在修正权值时,不仅要考虑误差在梯度上的作用,而且还要考虑在误差曲面上变化趋势的影响。
(2)改变学习速率。较大的学习速率能够在训练初期加快收敛过程,然而当误差较小时,过大的学习速率可能会越过误差最小值点,这样反而不利于最优值的求取。本文是在训练过程中逐渐减小学习速率。
2.3 神经网络识别
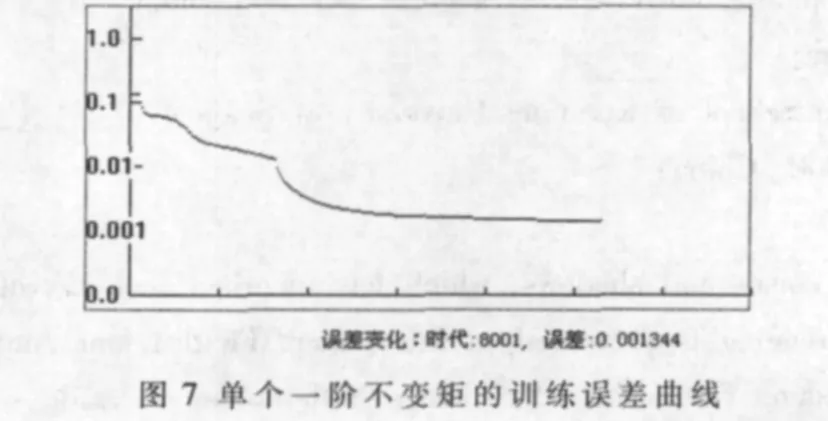
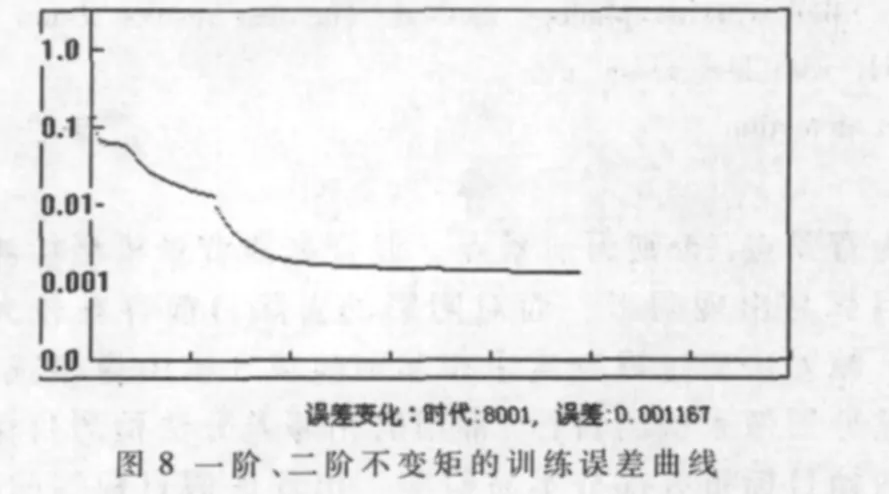
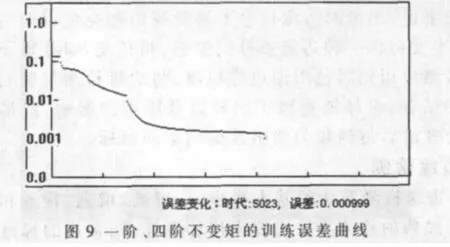
对每个子块,本文首先尝试选取三种特征类型:单个一阶不变矩,一阶、二阶两个不变矩以及一阶、四阶两个不变矩。有4种类别的训练样本,如图6所示,每种类别20个。测试图片每种类别10个,以两种不同摆放方式,共获取20张图片。程序基于VC++2008实现,主要分为训练与识别两部分[5]。训练误差曲线如图7~图9所示。
三种特征类型期望的最后误差都是0.001。可以看出,单独采用一阶矩作为特征在8001代时误差仍为0.001 344;采用一、二阶矩表现稍微好些,8001代时误差是0.001 167;而采用一、四阶矩时误差明显减小,在5 023代时,误差已经在0.001之下了。与训练相一致,测试时,4种瓷砖共80张测试样本,采用一阶不变矩特征出现两张误判,一、二阶不变矩组合两张误判,而一、四阶不变矩组合0张误判。由此可见,利用一、四阶距组合识别准确率很高。另外,每个瓷砖从特征提取到给出正确结果的时间为1 s,具有一定的实时性,能满足生产线上的需求。

本文系统地介绍了基于分块不变距特征的瓷砖分类识别的方法。利用形态学边缘检测提取瓷砖的花纹;再利用Hu不变矩针对部分不变矩不稳定的问题提出分块思想,分块后提取每个子块最稳定的不变矩作为本子块的特征,从而解决了分块后带来的位置相关性问题;最后用BP神经网络进行训练来分类识别。实验结果,表明此方法效果较好、速度快、准确率高,且对瓷砖的摆放位置不作要求,可以实现瓷砖在线生产上的分类识别的实时性的需求。该方法具有一定的通用性,对以矩作为特征的分类识别问题具有一定的参考意义。
[1]刘笛.墙地砖颜色的自动分类研究[D].广州:华南理工大学,2004.
[2]苏彩虹.墙地砖质量自动检测技术的研究[D].广州:华南理工大学,2004.
[3]郑力新,姚强,周凯汀.利用遗传算法实现模板匹配的瓷砖分选[J].华侨大学学报(自然科学版),2010,31(6):632-635.
[4]李国祥,张显全,秦芳远.基于不变矩和BP神经网络的剪纸纹样识别[J].计算机工程与应用,2010,46(29):158-60.
[5]张铮,王艳平,薛桂香.数字图像处理与机器视觉—Visual C++与 Matlab实现[M].北京:人民邮电出版社,2010.
[6]蒋宪刚.数字图像模式识别工程软件设计[M].北京:水利水电出版社,2008.
[7]韩力群.人工神经网络理论、设计及应用[M].北京:化学工业出版社,2007.

