基于CUDA架构矩阵乘法的研究

马梦琦，刘 羽，曾胜田

（桂林理工大学 信息科学与工程学院，广西 桂林541004）

随着多核CPU和众核GPU的快速发展，计算行业正在从只使用CPU的“中央处理”向CPU与GPU并用的“协同处理”发展，并行系统已成为主流处理器芯片。传统的GPU架构受其硬件架构的影响不能有效利用其资源进行通用计算，NVIDIA(英伟达)公司推出的统一计算设备架构 CUDA(Compute Unified Device Architecturem)，使得GPU具备更强的可编程性，更精确和更高的性能，应用领域也更加广泛。

矩阵乘法是一种大计算量的算法，也是很耗时的运算。CPU提高单个核心性能的主要手段比如提高处理器工作频率及增加指令级并行都遇到了瓶颈，当遇到运算量大的计算，CPU进行大矩阵的乘法就变得相当耗时,运算效率很低下。因此，GPU凭借其超强计算能力应运而生，让个人PC拥有了大型计算机才具备的运算能力。本文运用GPU的超强计算能力在CUDA架构上实现了大矩阵乘法。

1 CUDA架构

NVIDIA及时推出CUDA这一编程模型，在应用程序中充分结合利用CPU和GPU各自的优点，特别是GPU强大的浮点计算能力。CPU主要专注于数据高速缓存(cache)和流处理(flow control)，而 GPU更多地专注于计算密集型和高度并行的计算。尽管GPU的运行频率低于CPU，但GPU凭着更多的执行单元数量使其在浮点计算能力上获得较大优势[1]。当前的NVIDIA GPU中包含完整前端的流多处理器(SM)，每个SM可以看成一个包含8个1D流处理器(SP)的SIMD处理器。主流GPU的性能可以达到同期主流CPU性能的10倍左右。图1所示为GPU与CPU峰值浮点计算能力的比较。

CUDA的编程模型是CPU与GPU协同工作，CPU作为主机 (Host)主要负责逻辑性强的事务处理及串行计算，GPU作为协处理器或者设备(Device)负责密集型的大规模数据并行计算。一个完整的CUDA程序=CPU串行处理+GPU Kernel函数并行处理。

一个CUDA架构下的程序分为两个部分，即上述的Host端和Device端。通常情况下程序的执行顺序如下：Host端程序先在CPU上准备数据，然后把数据复制到显存中，再由GPU执行Device端程序来处理这些数据，最后Host端程序再把结束运算后的数据从显存中取回。

图2为CUDA编程模型，从中可以看出，Thread是GPU执行运算时的最小单位。也就是说，一个Kernel以线程网格Grid的形式组织，每个Grid由若干个线程块Block组成，而每个线程块又由若干个线程Thread组成。一个Kernel函数中会存在两个层次的并行，Grid中Block之间的并行和Block中Thread之间的并行，这样的设计克服了传统GPGPU不能实现线程间通信的缺点[2]。

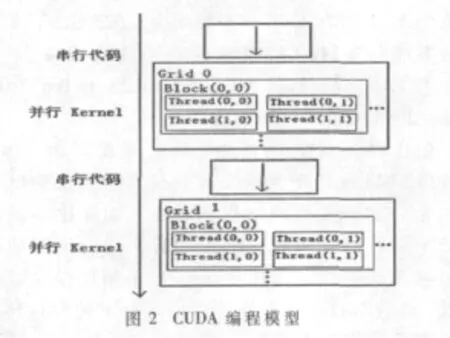
同一个Block下的Thread共用相同的共享存储器，通过共享存储器交换数据，并通过栅栏同步保证线程间能够正确地共享数据。因此，一个Block下的Thread虽然是并行的，但在同一时刻执行的指令并不一定都相同，实现了不同Thread间的协同合作。这一特性可以显著提高程序的执行效率，并大大拓展GPU的适用范围。

2 基于CUDA架构矩阵乘法的实现

2.1 一维带状划分

给定一个M×K的矩阵A和一个 K×N的矩阵 B，将矩阵B乘以矩阵A的结果存储在一个M×N的矩阵C中。此种矩阵乘法使用了一维带状划分，每个线程将负责读取矩阵A中的一行和B中的一列，矩阵进行乘法运算并将计算结果存储在全局存储器。

全局存储器会对矩阵A进行N次读取，对矩阵B进行M次读取。假设数组在每个维度上的尺寸都是BLOCK_SIZE的整数倍。若矩阵大小为32×32，则可表示为(2×16)×(2×16)。下面的内核定义中，结果矩阵 C中的每个元素由一个线程负责，for()循环完成A中第X行与B中第X列对应元素的乘加运算，并将结果累加到Cvalue。

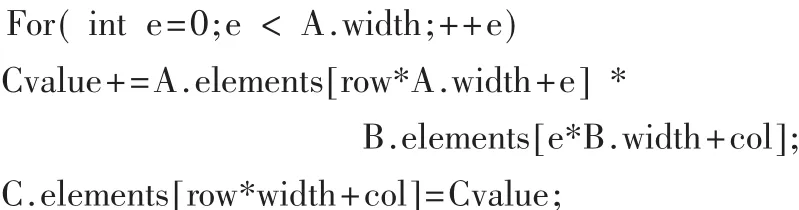
在矩阵相乘实现中，这个内核运算的速度不尽人意，主要瓶颈在于对内存的重复读取，计算量是 2×M×N×K flop，而全局内存的访问量为2×M×N×K B[3]。 若矩阵维数为 1 024×1 024，则此次矩阵相乘的计算量就有2 G flop，当矩阵维数更大时，这个运算量就相当大，在内存的读取上会浪费大量的时间。

2.2 二维棋盘划分

因为矩阵A的行和矩阵B的列多次被读取，为了避免重复加载，选择把矩阵进行分块运算，使用shared memory来实现矩阵乘法。运用shared memory的好处在于其延迟小于global memory，并且还能使线程间进行通信。矩阵A只被读了N/BLOCK_SIZE次，矩阵B仅被读了M/BLOCK_SIZE次，节省了大量的global memory带宽。

首先把划分的小矩阵块加载到share memory，则小矩阵本身的乘法就不用去存取外部的任何内存了，因此在二维棋盘划分中，矩阵乘法的计算量仍然是2×M×N×K flop，b是矩阵B划分的小矩阵块的大小，则全局内存访问量是 2×M×N×K/b B。

棋盘划分运算可以表示为：C矩阵的(0,0)～(15,15)=A(0～15,0～15)×B(0～15,0～15)+A(0～15,16～31)×B(16～31,0～15)+A(0～15,32～47)×B(32～47,0～15)+…+A(0～15,(16×(n-1)-1)～(16×(n-1))×B((16×(n-1)-1)～(16×(n-1)),0～15)。

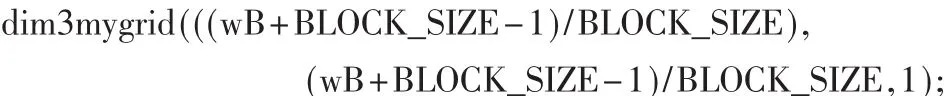
根据 NVIDIA CUDA Programming Guide，一个 Block里至少要有64个 Thread，最多有512个Thread。官方建议256个Thread是最合适的，因为此时有足够多的active warp有效地隐藏延迟，使得SM能够尽量满负荷工作[4]。为便于理解，假设矩阵为 n×n,此时 BLOCK_SIZE设置为 16，使用 dim3来设计，每个 Block包含 16×16个Thread，一个 Grid 共有(n/16)×(n/16)个 Block。

BLOCK_SIZE是不是越大越好呢？这样一个SM里的Thread就更多，虽然 Thread越多越能隐藏 latency，但G80/G92架构每个 SM上 shared memory仅有 16 KB，这会让每个Thread能使用的资源更少，效率反而会下降。

2.3 根据CUDA架构对矩阵乘法进行优化

因为棋盘划分中涉及到的是二维数组，cudaMalloc2D()能确保分配二维数组并且能分配适当的填充以满足对齐要求，还能确保在访问行地址或者二维数组与其他设备内存之间的数据复制能达到最佳性能。

二维棋盘划分方法仅限于数组大小必须是BLOCK_SIZE的整数倍，若矩阵维数并不是16的整数倍，则会造成运算效率的下降，此时可以利用CUDA架构特点和CUDA提供的cudaMallocPitch()函数来解决此问题。cudaMallocPitch()可以自动地以最佳倍数来分配内存。

呼叫Kernel部分需要修改成：

在数值分析，Kahan求和算法(也称作补偿总和)能显著减少浮点数运算的误差，在CUDA矩阵乘法中可以通过使用Kahan求和算法来提高计算精准度[5]。算法如下：

3 测试环境及实验结果

测试的硬件环境：CPU使用的是AMD Athlon II X2 245处理器,核心数为 2，该处理器主频为2.9 GHz，峰值运算能力约为17.4 GFLOPS；GPU使用的是NVIDIA GeForce 9800M GTS，有8个 SM即有 64个SP单元，显存带宽为51.2 GB/s，GPU核心频率为0.625 GHz，单精度浮点计算能力为240 GFLOPS，属于NVIDIA中端显卡。测试的软件环境：Windows XP系统，CUDA toolkit 3.0,Visual Studio 2008，CUDA计算能力为 1.1。

在程序运行的测试中，对矩阵规模由256×256～2 048×2 048逐渐增大，实验数据均是三次测试取得的平均值，这样实验的结果更准确。加速比是指程序在CPU上运行的时间与程序在GPU上运行所需的时间之比。峰值比是指运算速度与GPU单精度浮点运算能力之比。最后求得在各种矩阵规模运行下的加速比及峰值比。实验结果如表1所示。

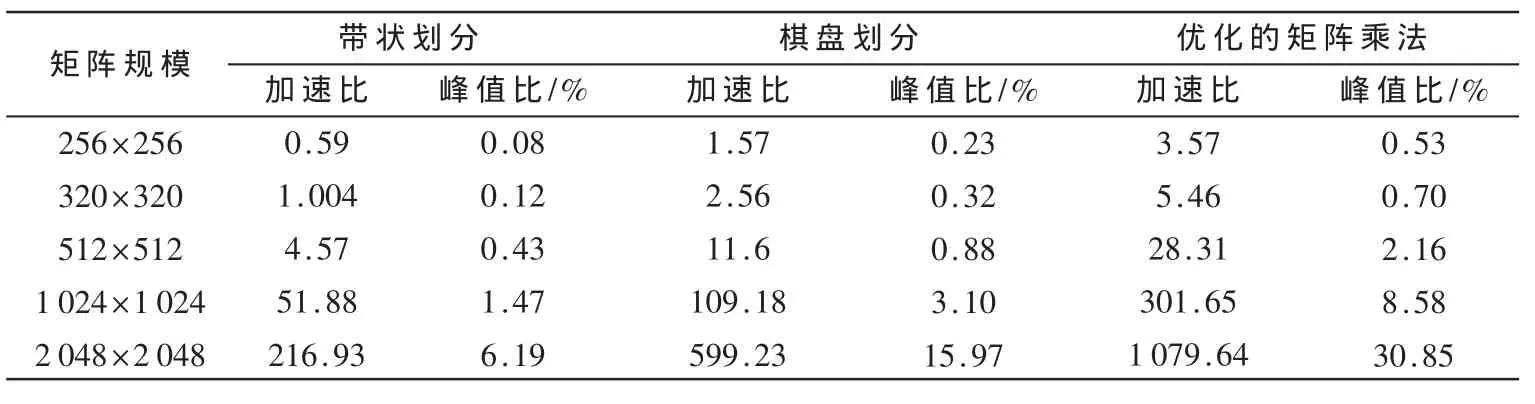
表1 不同矩阵规模的加速比及GPU峰值比

实验结果表明：当矩阵维数小于 320×320时，带状划分加速比小于1，说明CPU运算时间要小于一维带状划分时GPU的运算时间，这说明GPU计算时，从内存复制矩阵到显存和把结果矩阵从显存拷贝回内存过程中消耗了一些时间[6]。随着矩阵维数的增大，CPU的运算时间呈现级数增长，而GPU运算时间只是小幅度增长。此时GPU强大的浮点运算能力凸显出来，加速比在矩阵维数为2 048时最大为 1 079.64，CPU上Intel MKL矩阵乘法比文中所用的CPU矩阵乘法快了200多倍，但是依靠GPU流多处理的并行执行能力，GPU上的实现方法还是比Intel MKL快了5倍左右。运用CUDA的软硬件架构使得GPU合理组织数据，使得内存的读取节省了大量时间。峰值比也有很大的提高，峰值比说明了算法对GPU强大浮点运算能力的利用，对GPU相应算法的对比具有很高的参考价值。

通过矩阵乘法在CPU与GPU上不同的性能表现可以发现，NVIDIA公司推出的CUDA使某些大运算量的计算可以从大型计算机或者超级计算机转移到个人PC，这一新技术不仅使科研缩减了成本，同时也为科学领域进行大规模运算提供了新方法[7]。对于它的未来值得期待，毕竟CUDA已经在影视制作、计算金融、流体力学、医学成像、石油天然气数据收集、地质勘探及超级计算机的建立等领域取得了成功。

[1]NVIDIA Corporation.NVIDIA CUDA Programming Guide Version3.0[EB/OL].(2010-02-10)[2011-08-20].http://cuda.csdn.net/.

[2]张舒，褚艳利，赵开勇，等.GPU高性能并行运算之CUDA[M].北京：中国水利水电出版社，2009.

[3]Ye Zhenyu.GPU assignment 5KK70[DB/OL].(2009-11-05)[2011-09-01].http://wenku.baidu.com/view/9cd2e372027-68e9951e738e5.html.

[4]NVIDIA Corporation.NVIDIA CUDA CUBLAS library PG-00000-002_V3.0[EB/OL].(2010-02-10)[2011-09-10].http://cuda.csdn.net/.

[5]Hotball.深入浅出谈 CUDA技术[DB/OL].(2008-11-21)[2011-09-15].http://www.pcinlife.com/article/graphics/2008-06-04/1212575164d532_3.html.

[6]刘进锋，郭雷.CPU与GPU上几种矩阵乘法的比较与分析[J].计算机工程与应用，2011,47(19)：9-23.

[7]肖江，胡柯良，邓元勇.基于 CUDA的矩阵乘法和 FFT性能测试[J].计算机工程，2009.35（10）：7-10.