不同荷载比下嵌固式钢框架节点M-θr曲线拟合

索婉秋， 段树金

(石家庄铁道大学土木工程学院，河北石家庄050043)

0 引言

在钢结构设计中，节点的刚度有完全刚性、半刚性连接、理性铰接三类，自1917年，Wilson and Moore等人首次进行了对铆钉连接的柔性节点足尺实验至今，各国学者对不同的节点形式进行了广泛的实验研究和理论探讨。Frye和Morris，Jones Kirby和Nethercot，Kishi和Chen分别提出了自己的数学模型［1-3］，形成了方便设计采用的数据库。王新堂推导了具有任意半刚性连接空间梁系结构的计算模型，该模型可调整参数退化为完全刚接或理想铰接［4］。王燕等［5］推导了多种半刚性连接形式的内力计算公式，讨论了半刚性连接对框架内力的影响。

通常提到的半刚性连接其形式为栓接、铆接、焊接、栓焊混接，文献［6］和文献［7］借鉴古代榫卯构造的特点和现代钢结构技术，提出了一种新型嵌固式节点形式，其空间框架模型图及其构件图见图1。该节点可称为榫卯节点的一种。其由榫头和卯孔组成，通过榫头和卯孔的相互嵌固咬合，使得节点可以承受一定的荷载，并且具有良好的弹性和刚度，表现为较强的半刚性特性。现主要对这种嵌固式节点的受力性能进行探讨，在有限元分析的基础上提出嵌固式节点的数学模型。

图1 嵌固式组装空间框架模型与其构件形式图

1 嵌固式门式框架有限元分析

1.1 嵌固式门式框架有限元模型的建立

嵌固式组装钢框架的缩尺模型实验于2009年7月在石家庄铁道大学结构实验室进行。其中X方向框架的梁是两根方钢管水平并联组成，Y方向框架的梁是由两根方钢管竖向叠合组成，X方向框架的柱截面与Y方向框架的相比刚好旋转90°。通过对实验数据的分析和整理可以看出嵌固式节点的刚度在初期受力时有一短暂的不稳定阶段［6-8］。由于模型实验受到限制，采用仿真分析的方法对其进行多种荷载组合条件下的加载分析。首先对框架中不同部位的节点进行了数值仿真分析，并将仿真分析值与实验值进行比较，比较结果显示嵌固式节点的仿真分析所得结果与实验值基本吻合，从而验证了嵌固式节点仿真模型的可靠性［9］。在此基础上，建立具有嵌固式节点的门式框架仿真模型。门式框架仿真模型借鉴节点仿真模型对于材料属性的定义和单元选取上的经验。采用理想弹塑性本构关系和Von-Mises屈服准则，选用的单元有SHELL181壳单元、CONTA173和TANGE170接触单元。

门式框架有限元模型的边界条件和加载方式与节点的有所不同，其ANSYS分析模型如图2和图3所示。其中ρ为竖向荷载和水平荷载的比值，即ρ=Fv/Fh。在门式框架中，将两个小短梁的一端全部约束，限制框架平面外变形。采用单调加载方式加载，定义了6种荷载工况。对于只有竖向荷载参与的荷载工况，最终的竖向荷载值为250 kN;对于只有水平荷载作用的情况，最终的水平荷载值为150 kN。

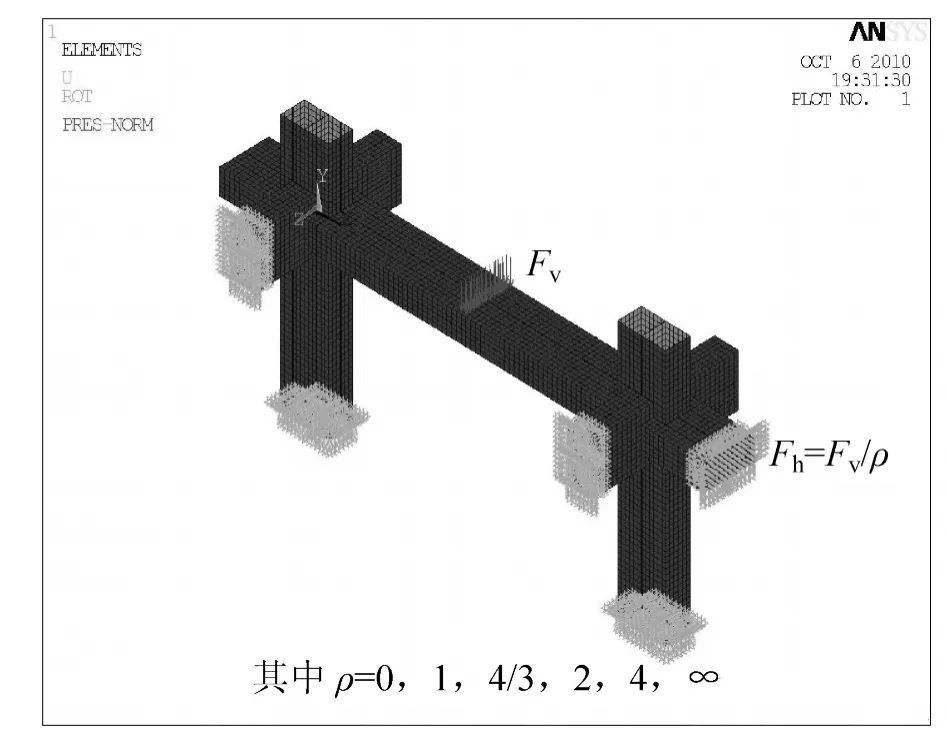
图2 X方向门式框架加载模型

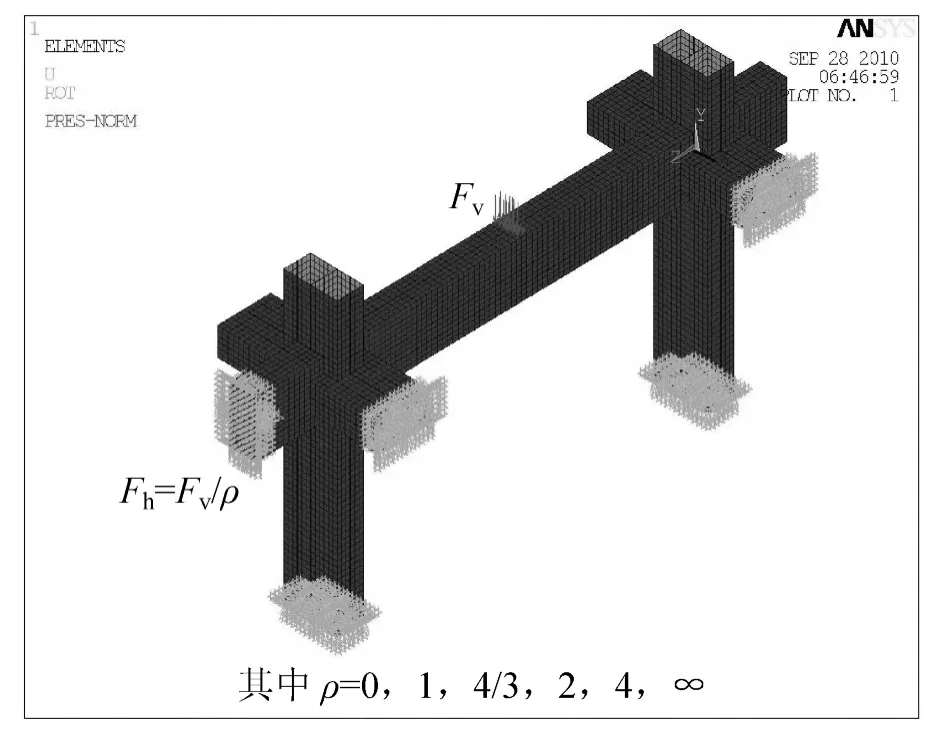
图3 Y方向门式框架加载模型

1.2 数值模拟结果分析

对不同的荷载组合进行分析。图4、图5分别表示X、Y方向框架在不同荷载组合情况下的弯矩—转角关系。

从图4和图5中可以看到，节点M-θr关系严重依赖于比值ρ;当竖向荷载很小时，节点近似于铰接。在加载之初，其节点刚度几乎为零，接近于铰接节点，这是由于设置的榫卯间隙所致。节点的弯矩有一个不稳定的过程，说明节点处由于荷载的不断增大，缝隙逐渐被压紧，使得节点的受力状态发生了变化，从而使得节点刚度有一定的变化。当水平荷载和竖向荷载共同作用时，节点内部的各单元处于双向或三向应力状态中，促进了节点处缝隙进一步压紧密实，其节点刚度要比单独竖向荷载作用时有所增加。两个方向框架由于其构造不同，荷载组合对节点刚度的影响也不同。

2 节点M-θr曲线拟合

根据仿真分析所得弯矩—转角曲线特性，所提出的数学模型应该满足以下基本条件［10］:

(1)曲线应过原点，即当θr=0时，M=0;

(2)曲线在原点处的斜率应该等于该节点连接的初始刚度Ki，即当θr=0时，d M/dθr=Ki;

(3)当转角变得很大，极端情况是当转角趋于无穷大时，曲线的斜率接近于节点的破坏刚度Kp，即当θr→∞时，d M/dθr=Kp;此时所对应的弯矩值应为该节点的极限弯矩，即M=Mp;

图4 X方向框架不同荷载组合下的M-θr曲线

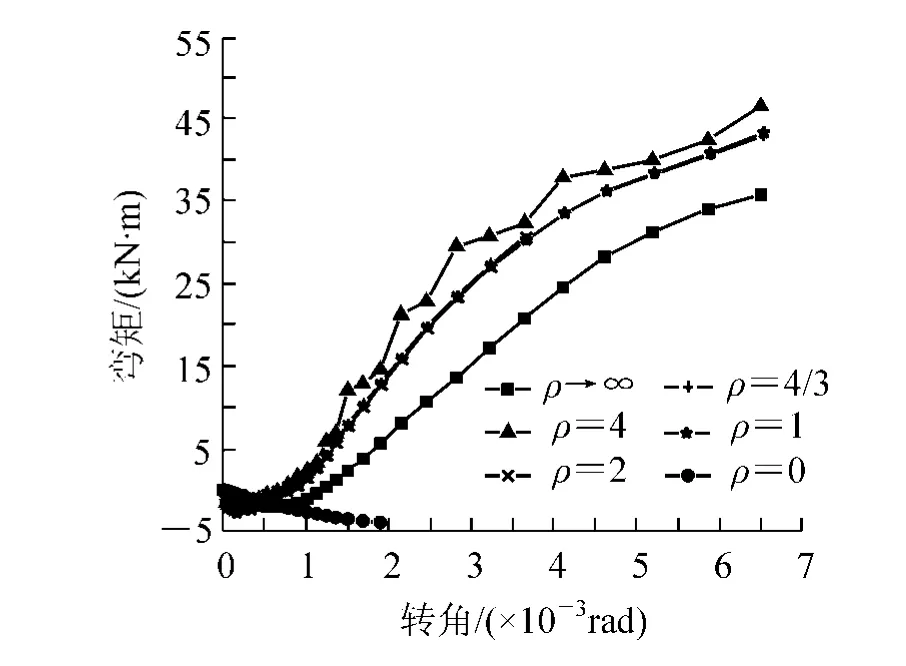
图5 Y方向框架不同荷载组合下的M-θr曲线

(4)任意给定一个转角值，表达式都应该有唯一的一个刚度值与其对应，也应有唯一的弯矩值与其对应。

(5)在满足参数具有一定物理意义的前提下，曲线的表达式应尽可能简洁。

在公式的拟合过程中，将嵌固式节点的几何位移扣除，得到其半刚性的相对转角θr作为拟合公式的自变量

式中，θr为节点处的相对转角;θ为节点处的总转角;θΔ为节点处的几何位移引起的转角。

几何位移的影响是通过实验测定的。荷载工况条件不同则几何位移也不同。

2.1 两个方向框架节点复杂指数函数形式的M-θr曲线拟合

2.1.1 X方向框架节点M-θr曲线拟合

结合上述所提到的各参数的物理意义，假设X方向框架节点M-θr曲线表达式为

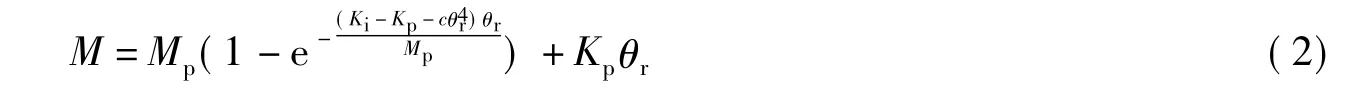
式中，θr为自变量，θr∈R;参数Mp、Ki、Kp、c与荷载比值ρ之间的关系(0≤ρ≤4)为

将不同荷载工况作用下(0≤ρ≤4)所得的Mp、Ki、Kp、c代入公式(2)，即可以得到节点的M-θr曲线关系。

当只有竖向荷载作用时，即ρ→∞时，对于式(2)中的参数要根据实验数据单独拟合，拟合结果如下

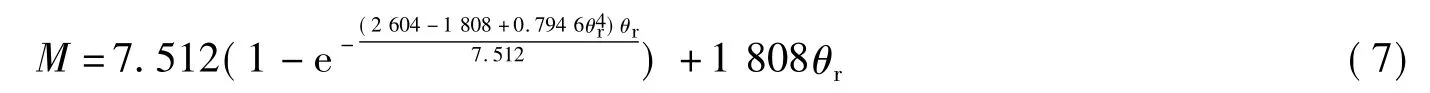
2.1.2 Y方向框架节点M-θr曲线拟合

设Y方向框架节点M-θr曲线表达式为

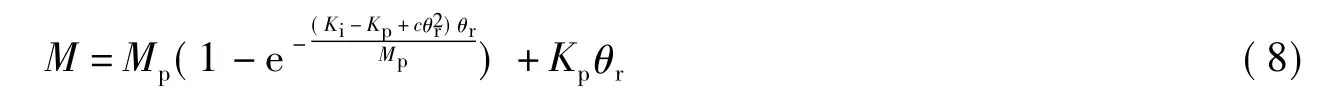
式中，θr为自变量，θr∈R;参数Mp、Ki、Kp、c与荷载比值ρ之间的关系(0≤ρ≤4)为

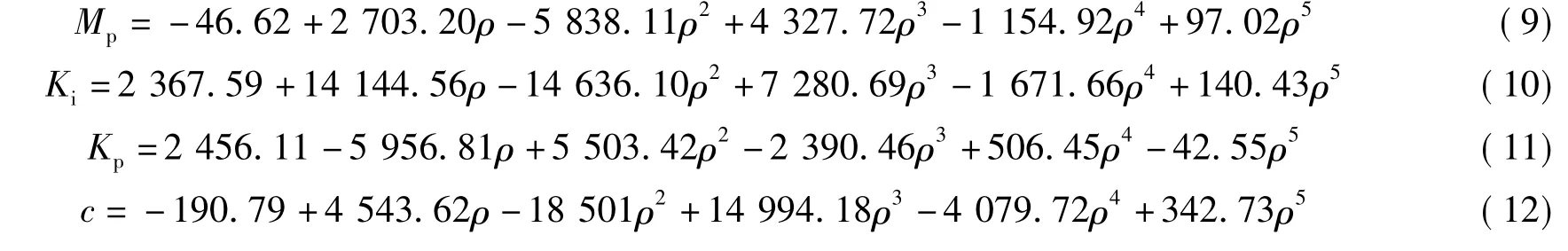
将不同荷载工况作用下(0≤ρ≤4)所得的Mp、Ki、Kp、c代入公式(8)，即可以得到节点的M-θr曲线关系。

ρ→∞当时，此时只有竖向荷载作用，对于式(8)中的参数要根据实验数据单独拟合。此时节点的M-θr关系可表示为

2.2 两个方向框架节点其他函数形式的M-θr曲线拟合

从公式的简化考虑，不严格考虑各系数的物理意义，对两个方向框架的M-θr关系采用了较为简单的指数函数和二次多项式拟合。

2.2.1 简单指数函数形式的节点M-θr曲线拟合

对于X、Y方向框架，设指数拟合公式为

式中，αi、βi为系数，其值的确定与荷载比值ρ有关。i的取值为X、Y。

当0≤ρ≤4时，X方向框架，αX、βX的确定参见公式(15)、(16);Y方向框架，αY、βY的确定参见公式(17)、(18)。

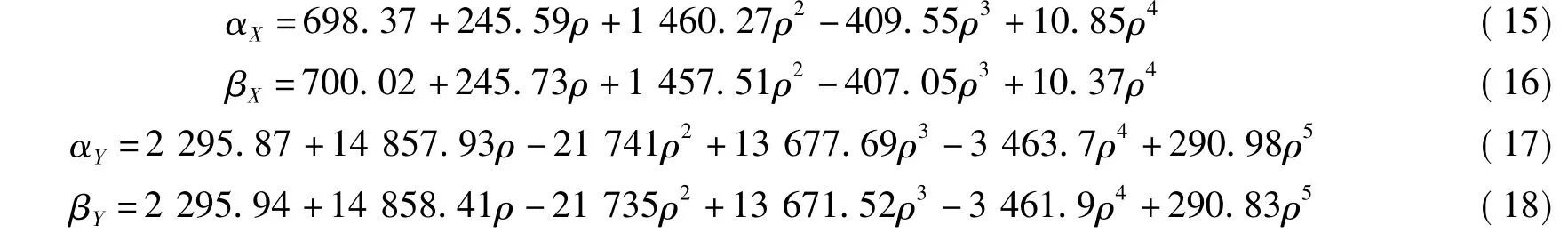
将以上所得参数带入公式(14)，可以得到0≤ρ≤4时，嵌固式节点的M-θr曲线关系。

当ρ→∞时，对于式(14)中的参数要根据实验数据单独拟合。此时X、Y方向嵌固式节点的M-θr关系中系数的取值分别为:αX=－2 160;βX=2 162。αY=－7 297;βY=7 299。

2.2.2 二次多项式形式的节点M-θr曲线拟合

对于X、Y方向嵌固式节点，设二次多项式拟合公式为

式中，lj、tj为系数，其值的确定与荷载比值ρ有关。j的取值为X、Y。

当0≤ρ≤4时，X方向框架，lX、tX参见公式(18)、(19);Y方向框架，lY、tY参见公式(20)、公式(21)。

将以上所得参数带入公式(17)，可以得到0≤ρ≤4时，嵌固式节点的M-θr曲线关系。

当ρ→∞时，对于式(17)中的参数要根据实验数据单独拟合。此时X、Y方向嵌固式节点的M-θr关系中系数的取值分别为:lX=－2 730;tX=－21 260。lY=7 742;tY=－6 320。

2.3 方差分析与比较

通过嵌固式节点非线性仿真分析，得到6种荷载组合情况下，嵌固式节点的M-θr曲线，对其进行非线性回归分析，得到了公式(2)～公式(21)。为阐明所拟合曲线与实验值之间的相关性，计算两者的相关指数R2

式中，Mi为仿真实验弯矩值;为公式计算所得弯矩值;为仿真实验所得弯矩值的平均值。

计算结果显示，三种拟合公式的相关指数R2都在0.9以上，公式的可用性较强。但三种拟合公式各有其特点，采用复杂指数函数拟合时，考虑了各参数的物理意义，且拟合程度也是三种方程中最好的，0.948 8≤R2≤0.996 4;而采用简单指数函数和二次多项式拟合，形式简洁，使用方便，拟合程度也较高，其相关指数取值范围分别为0.940 2≤R2≤0.990 4和0.925 3≤R2≤0.997 7。在应用时可以根据具体需要采用。三种拟合公式对X方向框架节点M-θr曲线的拟合程度参见图6～图11。

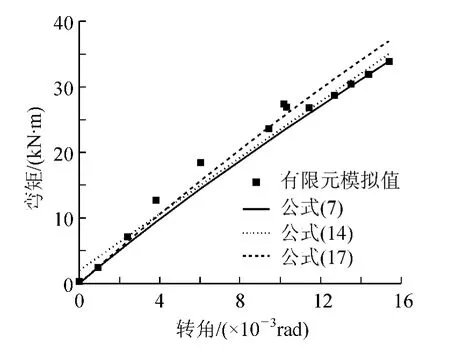
图6 ρ→∞时X方向框架节点M-θr曲线对比

图7 ρ=0时X方向框架节点M-θr曲线对比

图8 ρ=1时X方向框架节点M-θr曲线对比

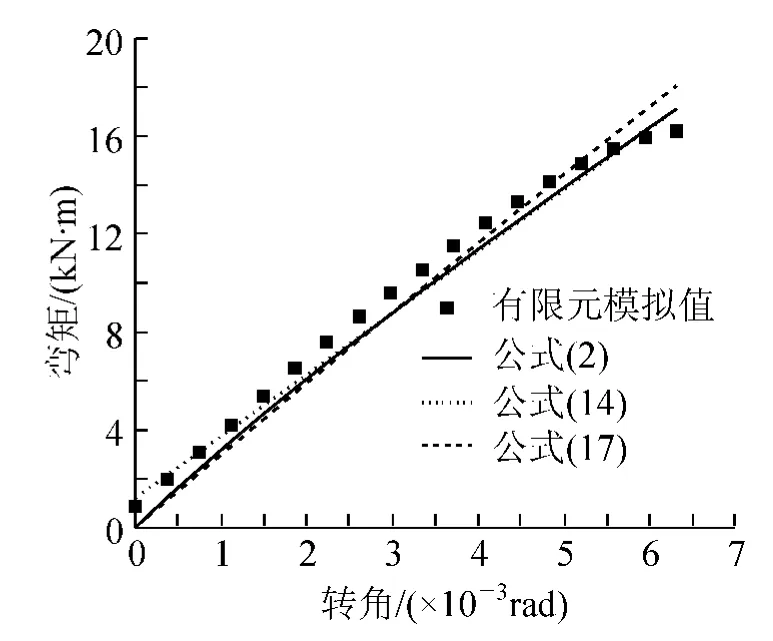
图9 ρ=1.3时X方向框架节点M-θr曲线对比

图10 ρ=2时X方向框架节点M-θr曲线对比

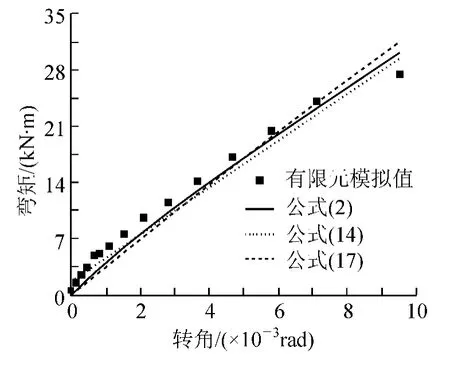
图11 ρ=4时X方向框架节点M-θr曲线对比

从图6～图11可以看出，简单指数函数拟合曲线，在转角θr=0时，所对应的弯矩并不都为零。当公式中的αX、βX为特定值时，才有可能使公式满足当θr=0时，M=0的条件。简单指数函数和二次多项式相对于复杂指数函数，其拟合程度相对较低，但公式形式简洁，使用方便。

三种拟合公式对Y方向框架节点M-θr曲线的拟合程度参见图12～图17。

从图12～图17可以看出，简化指数函数所拟合曲线，在转角θr=0时，M≠0。当公式中的αY、βY为特定值时，才能使公式满足当θr=0时，M=0的条件，这是该公式的一个弊端;简化的指数函数、二次多项式与复杂指数函数相比，其拟合程度相对较低，但可操作性增强。

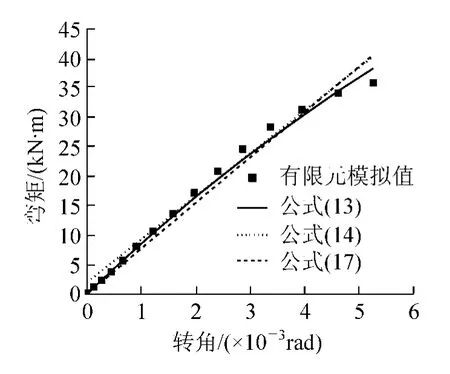
图12 ρ→∞时Y方向框架节点M-θr曲线对比

图13 ρ=0时Y方向框架节点M-θr曲线对比

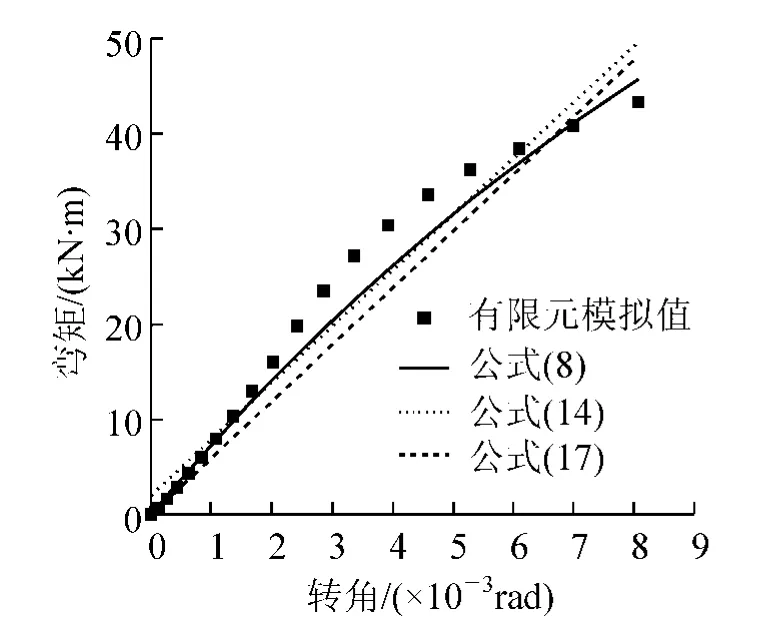
图14 ρ=1时Y方向框架节点M-θr曲线对比

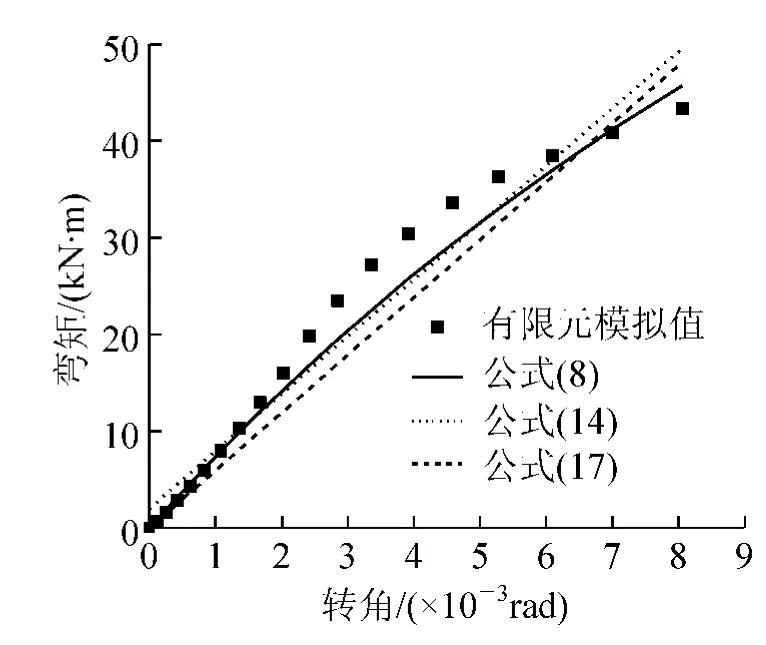
图15 ρ=1.3时Y方向框架节点M-θr曲线对比

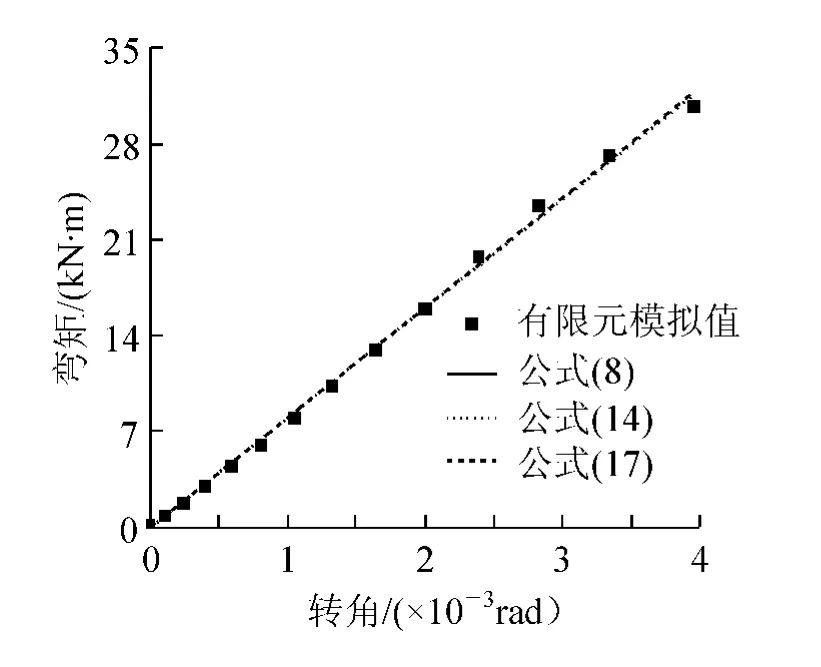
图16 ρ=2时Y方向框架节点M-θr曲线对比

图17 ρ=4时Y方向框架节点M-θr曲线对比

3 结论

(1)鉴于嵌固式节点构造的特殊性，利用ANSYS软件提供的丰富的单元库，采用接触单元和壳单元相结合的方法，对嵌固式组装钢框架进行有限元数值仿真，可以较为真实的反映节点区域的受力性能，对此类问题的数值模拟有一定的借鉴作用。

(2)通过不同的荷载组合，分别得到了两个方向框架的6组弯矩-转角关系曲线的仿真实验数据。利用这6组数据对两个方向的框架分别进行了数学模型拟合。从公式的相关指数可以看出，两个方向框架拟合匹配度较好。对于公式中参数的物理意义的考虑及其拟合，可为以后的研究提供借鉴和帮助。

本文只是对在不同荷载比下嵌固式组装钢框架中嵌固式节点的力学特性进行了初步探讨。对于嵌固式组装钢框架还应进行更加全面和深入的研究:

(1)可以继续利用数值仿真模拟研究节点形式、结构尺寸、管壁厚度以及构造间隙等因素对嵌固式节点刚性的影响，丰富实验数据，找出其中的内在规律，为其付诸于实践提供理论依据。

(2)可以建立整体空间框架模型，对其进行加载和动力特性的模型实验以及有限元数值仿真，更进一步研究榫卯构造节点对框架整体受力性能的影响。

(3)可以尝试对嵌固式节点进行优化设计，从多个方面完善这种特殊节点构造的半刚性框架的设计理论。

［1］NETHERCOT D A.Utilization of experimentally obtained connections data in assessing in the performance of steel frame［J］.Proceedings ASCE，1985，27(3):13-37.

［2］GOVERDHAN A V.A collection of experimental moment-rotation curves and evaluation of prediction equations for semi-rigid connections［D］.Nashville:Vanderbilt University，1984.

［3］CHEN WF，KISHI N.Semi-rigid steel beam-to-column connections:data base and modeling［J］.Journal of Structural Engineering，1989，31(2):235-241.

［4］王新堂.任意半刚性连接空间梁单元的显式刚度［J］.空间结构，2003，9(3):33-37.

［5］王燕，李华军，厉见芬.半刚性梁柱节点连接的初始刚度和结构内力分析［J］.工程力学，2003，20(6):65-69.

［6］李猛.一种嵌固式组装钢框架的模型实验研究［D］.石家庄:石家庄铁道大学土木工程学院，2010.

［7］段树金，喻岩，李猛，等.一种榫卯连接方钢管组装框架模型的荷载位移曲线试验研究［J］.石家庄铁道大学学报:自然科学版，2010，23(2):16-20.

［8］索婉秋.嵌固式节点受力性能分析［D］.石家庄:石家庄铁道铁道大学土木工程学院，2011.

［9］DUAN SHUJIN，SUO WANQIU，YU YAN，et al.Model test on a kind of assembly steel frame with mortise and tenon［C］//The sixth proceedings of the International Strucrural Engineering and Construction socirty.Zurich:Research Publishing Servives，2011:721-726.

［10］YEE Y L，MELCHERS R E . Moment-rotation curves for bolted connections［J］. Journal of Engineering Structures，1986，112 ( 3) : 615-633.