钢-混凝土双面组合连续箱梁负弯矩区有限元分析
段树金, 董坤杰, 李鹏飞
(石家庄铁道大学土木工程学院,石家庄050043)
0 引言
在大跨连续梁桥中,采用双面组合箱形截面具有优势[1-2]。文献[3]构造了一种双面组合箱梁截面,并对连续梁的内力分析和截面承载力计算方法进行了研究。文献[4]在对双面组合箱梁负弯矩区力学行为进行模型试验的基础上,对将这种截面形式应用于铁路桥梁设计的若干问题进行了探讨。鉴于组合梁受力分析的复杂性,学术界和工程界都开展了对连续组合梁结构的数值仿真研究[5-10]。
建立集中力作用下双面组合连续箱梁负弯矩区的数值模型,对其受力性能进行研究,并与相应的П形组合梁和U形组合箱梁结构性能做比较。所研究的连续梁在集中荷载作用下负弯矩区的受力性能可由对称性建立如图1所示的计算模型,归结为一悬臂梁模型;图2为本文采用的双面组合箱梁截面。
1 截面刚度与强度
1.1 组合箱梁截面的刚度

图1 负弯矩区结构计算简图
如图3所示,梁截面处于线弹性状态,其高度为h;钢梁高度为hs,截面面积为As,绕其形心轴的惯性矩为Is,钢梁截面形心轴至下翼缘底面的距离为ys;上翼缘混凝土板中受拉钢筋的面积为Ar,上混凝土板钢筋合力作用点到顶部的距离为a;钢材和混凝土的弹性模量之比为αE;中和轴至梁底的高度为x。
不计混凝土抗拉强度,但考虑混凝土中受拉钢筋的作用,中性轴一般位于钢梁腹板内,按换算截面法和受力平衡可以得到负弯矩区截面的换算截面惯性矩I为
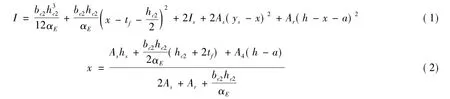
组合箱梁的截面刚度可表示为


图2 双面组合箱梁横截面

图3 组合箱梁截面及应力、应变图
1.2 组合箱梁截面塑性极限抗弯承载力
1.2.1 基本假定
在完全抗剪连接下,箱型截面组合梁截面塑性抗弯承载力计算中引入如下基本假定:(1)钢梁和混凝土板受弯时均符合平截面假定;(2)混凝土翼板与钢梁之间的栓钉有足够的强度,能够保证两者之间力的传递;(3)不考虑受拉上混凝土板混凝土的抗拉能力,但考虑板中纵向受拉钢筋的作用并达到塑性设计强度fy;(4)受压下混凝土板在塑性状态时截面应力均达到抗压设计强度fc;(5)钢梁在受拉区和受压区也采用矩形应力图,并分别达到钢材的塑性设计强度fsy。
1.2.2 极限弯矩
(1)中和轴位于钢梁腹板。塑性中和轴位置在钢梁内,设负弯矩区截面塑性中和轴高度y,根据受力平衡条件2fsy(twy+bftf)+bc2hc2fc=Arfy+2fsy[(hs-2tf-y)tw+bftf],可求得
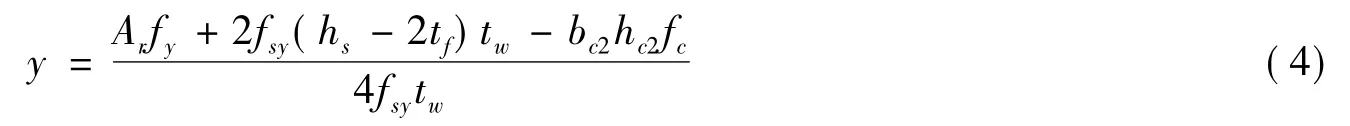
此时负弯矩区组合截面应力分布如图4所示,根据合力等效原则将组合截面应力分布分解为钢梁的抗弯能力Ms与附加弯矩M'之和,即
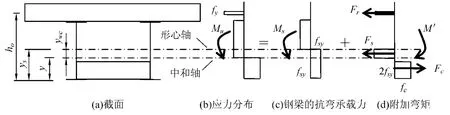
图4 中和轴位于钢梁腹板时的截面与应力分布

对Fs取矩,可得

式中,Fr为上翼缘混凝土板中纵向钢筋的合力,Fr=Arfrp;Fc为受压下翼缘混凝土板的合力;Wpx为钢梁对其下边缘的塑性截面抵抗矩;y为钢梁截面的塑性中和轴到下翼缘混凝土板底面的距离;ywc为钢梁截面的塑性中和轴和组合截面塑性中和轴之间的距离;hc2为下翼缘混凝土板厚度。
(2)中和轴位于下混凝土板中。塑性中和轴位置在下混凝土板内,设负弯矩区截面塑性中和轴高度y,根据受力平衡条件2fsy(twy+bftf)+bc2yfc=Arfy+2fsy[(hs-2bf-y)tw+bftf],可求得

此时负弯矩区截面和应力分布如图5所示。Mu的计算与前述类似,但

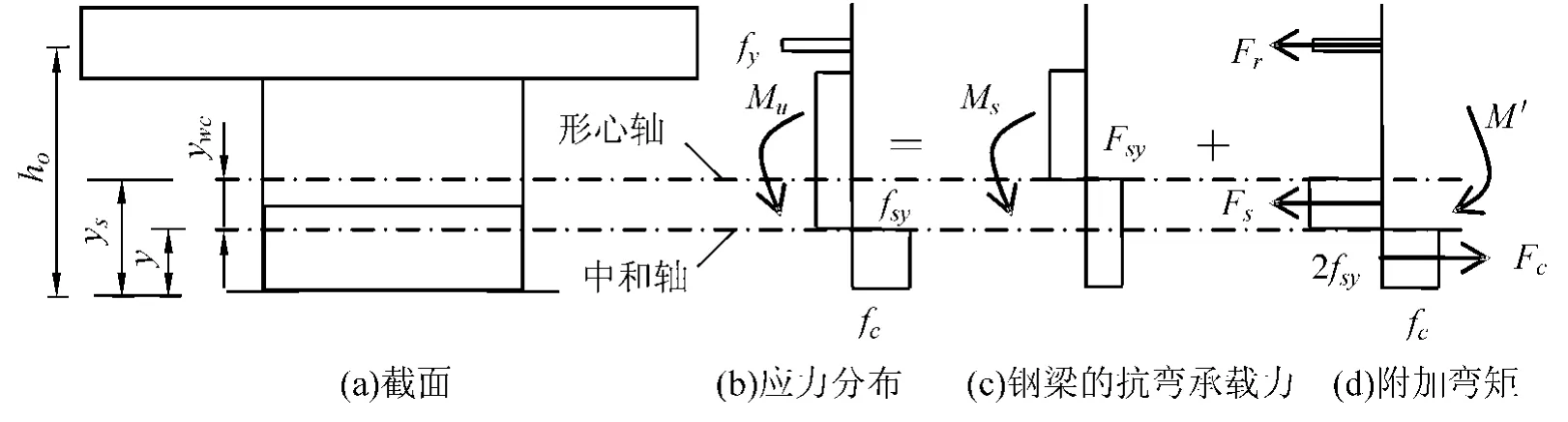
图5 中和轴位于钢梁腹板时的截面与应力分布
2 有限元数值分析
2.1 有限元模型的建立
参照文献[3]、文献[4],本文取钢-混凝土双面组合连续箱梁模型的负弯矩区长度为10 m,每隔2 m设置加劲肋板,5 m处设置横隔板。混凝土板厚为200 mm,其材料参数取自文献[11];钢梁部分采用HPB235;栓钉规格Ф13×80(公称直径13 mm,高度80 mm),布置间距为250 mm。上混凝土板配筋为双层14Φ12,下混凝土板配筋为双层7Φ12。单个钢梁截面面积为310 cm2,单位质量为241.8 kg/m。
数值分析采用Ansys的空间模型,混凝土采用实体单元Solid65建模,钢梁采用塑性大应变壳单元Shell43建模,栓钉由非线性弹簧单元Combin39模拟,网格划分如图6所示。

图6 双面组合箱梁有限元模型网格划分
(1)混凝土。混凝土本构关系中的相关参数取值如表1所示。受压混凝土应力-应变曲线根据《混凝土结构设计规范(GB50010—2002)》的公式确定。

表1 混凝土本构关系参数表
双面组合箱梁的负弯矩区上混凝土板均处于受拉状态,但是Ansys中Soild65定义应力-应变曲线时,受拉混凝土和受压混凝土的应力应变曲线是反对称的。这样就不符合双面组合箱梁上混凝土板受拉的实际状态,所以在此为受拉混凝土定义了一条单独的应力应变曲线。受拉区混凝土的应力应变曲线采用多线性随动强化MKIN模型。此模型最多允许5个应力、应变数据点,最多5条温度相关曲线。
混凝土的破坏准则采用Willam-Warnke的五参数破坏准则,即单轴抗拉强度、单轴抗压强度、双轴抗压强度、围压压力、在围压作用下的双轴及单轴抗压强度5个参数来判断。
(2)钢梁和钢筋。钢梁和钢筋都采用理想弹塑性模型,屈服准则采用了等向强化Mises屈服准则。钢材屈服强度统一取f=235 MPa。受压与受拉时弹性模量相同,Es=2.06×105MPa,泊松比v=0.3。
(3)栓钉。栓钉的纵向抗剪刚度由应用比较广泛的公式确定[5]

式中,m,n为模型参数,取m=0.989,n=1.535 mm-1;s为滑移量;Vu为栓钉的极限承载力,Vu=74.1 kN;γ为栓钉材料抗拉强度最小值与屈服强度之比,本文中取1;f为栓钉抗拉强度设计值。因为一般情况下有限元分析得到的滑移量不会超过规定的极限值,所以负弯矩区建模中未考虑栓钉的破坏准则。
2.2 计算结果与分析
利用上述方法建立双面组合箱梁负弯矩区的有限元模型,对梁从零逐级加载直至破坏进行了全过程数值仿真,得到的荷载挠度曲线如图7所示;主要结果数值与理论计算的比较见表2。在荷载分别加载到560 kN(弹性状态)和920 kN(塑性状态)时,中支座处横截面的应变分布见图8。

图7 双面组合箱梁负弯矩区荷载挠度曲线

图8 中支座处截面应变分布

表2 主要结果比较
(1)从图7可以看出,在荷载加至约130 kN和210 kN时,荷载位移曲线出现短暂波动,是由于上混凝土板两度受拉开裂所致;在荷载加至约560 kN时,弯矩最大截面钢梁上翼缘首先屈服;此后随着塑性区域增大,中和轴不断下移,截面刚度逐渐减小,挠度加速增长,直至破坏。
(2)从图8可以看出,截面应变在钢梁与混凝土板的交界面处发生突变,即钢梁和混凝土板的交界面产生了相对滑移。
(3)从表2看出,对极限弯矩,理论计数值大于数值计算值,其主要原因在于数值分析中没有考虑上混凝土板开裂后钢筋的贡献(整体式模型);数值计算时并不能达到理想的全断面屈服状态(包括先发生钢梁失稳)。
(4)本算例中,即使在弹性阶段,数值计算挠度也大于理论计算挠度,说明滑移引起的附加挠度不容忽视(本算例所取栓钉刚度偏小),也说明栓钉剪切刚度取值的重要性。
2.3 与普通组合梁的比较
П形组合梁(也称双主梁组合梁)与双面组合箱梁相比不设下混凝土板,其有限元模型如图9所示。

图9 П形组合梁有限元模型及网格划分
U形钢主梁组合箱梁是桥梁工程界采用较多的一种普通组合梁,本文所取模型是将双面组合箱梁模型中的下混凝土板用钢板(厚度同翼板)替代,其它参数不变。其有限元模型见图10。

图10 U形组合梁有限元模型及网格划分
将双面组合箱梁、П形组合梁和U形组合箱梁的荷载挠度曲线作比较见图11,承载能力的比较如表3所示。从中可知双面组合箱梁的承载能力无论是在弹性阶段还是在塑性阶段都优于П形组合梁和U形组合箱梁;双面组合箱梁的变形能力也优于П形组合梁和U形组合箱梁,充分体现了双面组合连续箱梁这种新型结构在承载能力和变形能力等方面的优越性。

表3 各种组合梁承载能力比较
3 结论
给出了一种钢与混凝土双面组合梁在负弯矩作用下截面刚度和极限弯矩的计算公式;建立了组合连续梁负弯矩区段的有限元分析模型。极限承载力的仿真计数值大于理论值约11.5%;而挠度的仿真计数值则小于理论值约20%,其差别主要源于基本假定有所不同。
用算例与U形组合箱梁和П形组合箱梁的仿真计算结果相比较,发现双面组合箱梁的承载能力分别高出6.5%和21.7%;刚度与变形能力明显增强;抗扭和防治平面外失稳的能力具有优势(本文未作讨论),证明了双面组合箱梁结构的合理性和优越性。

图11 三种组合梁的荷载挠度曲线比较
[1]Reiner Saul.Bridges with double composite action[J].Structural Engineering International,1996(1):32-36.
[2]David Collings.Double composite steel-concrete bridges[J].Bridge Engineering ICE,2008,161:45-48.
[3]郑浩,段树金.钢-混凝土组合箱梁力学分析[J].石家庄铁道学院学报,2009,22(2):11-14.
[4]Kim Hyun-Ho1,Shim Chang-Su.Experimental investigation of double composite twin-girder railway bridges[J].Journal of Constructional Steel Research,2009,65(6):1355-1365.
[5]王连广,李立新,刘之洋,等.钢与混凝土组合梁非线性全过程分析[J].东北大学学报,2001,22(1):51-53.
[6]宗周红,车惠民,房贞政.预应力钢-混凝土组合梁有限元非线性分析[J].中国公路学报,2000,13(2):48-51.
[7]周凌宇,余志武,蒋丽忠.钢-混凝土连续组合梁非线性有限元分析[J].长沙铁道学院学报,2003,21(2):9-13.
[8]段树金,霍军会,安蕊梅.钢-混凝土双面组合连续梁承载能力研究[J].铁道学报,2010,32(5):82-87.
[9]段树金,霍军会,周庆东.钢-混凝土双面组合梁极限承载力计算方法研究[J].石家庄铁道学院学报:自然科学版,2007,20(4):1-5.
[10]Fragiacomo M,Amadio C,Macorini L.Finite-element model for collapse and long-term analysis of steel-concrete composite girders[J].Journal of Structural Engineering ASCE,2004,6(2):1206-1213.
[11]段树金,周庆东,王海良,等.钢-混凝土双面组合连续的承载能力试验研究[J].铁道科学与工程学报,2008(25):12-17.

