基于全阶磁链观测器的异步电机无速度传感器矢量控制系统

李立明 刘忠举

（1 江西铜业股份有限公司德兴铜矿，德兴334224；2 中国船舶重工集团公司第七一二研究所，武汉430064）

1 引言

在异步电机的矢量控制中，磁链观测直接影响磁链的控制。磁链观测误差会通过控制使电机的磁链偏大或者偏小，从而导致电机效率降低或者过流。如何提高磁链观测的准确性是目前研究的主要方向。应用比较广泛的电压模型，由于其积分器带来的初值问题与积分偏移难以解决，采用改进积分器[1]后在基速范围内控制效果较好，但是算法在弱磁阶段将失效。由于电压模型没有利用到转速信号，故很难靠自身实现带速启动功能。本文在基于TMS320F2407的电机控制平台上实现了异步电机的自适应磁链观测的设计和实验验证。异步电机全阶磁链观测器作为一种闭环观测器，提高了磁链的观测精度，不存在弱磁的局限，能够很好的实现带速的平稳启动，且具有对参数变化的自适应能力和对参数误差的鲁棒性。

2 全阶磁链观测器原理

异步电机矢量形式的动态数学模型【2】基本描述公式：

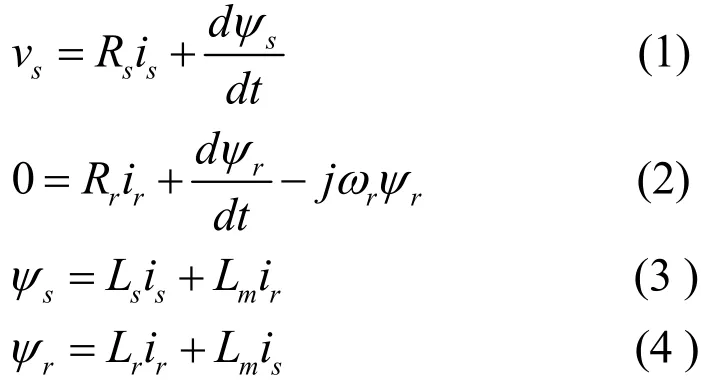
由上述电机模型可以推导得到以定子磁链φrα，φrβ和转子磁链φrα，φrβ为状态变量的电机模型矩阵方程[3]

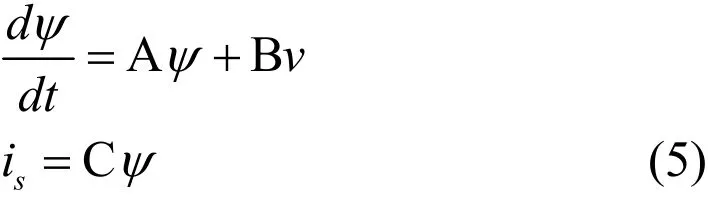
其中：

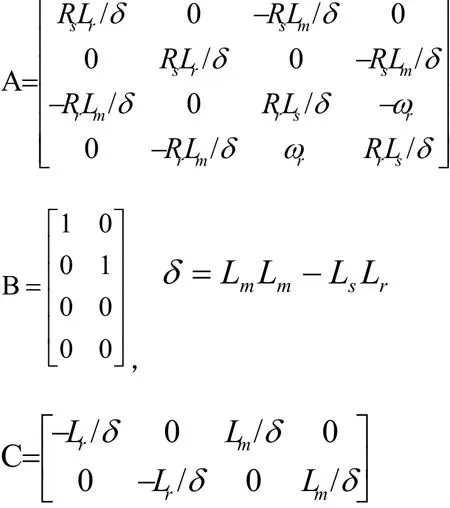
同时观测定子磁链和定子电流的全阶磁链状态观测器，可以用下面公式描述：

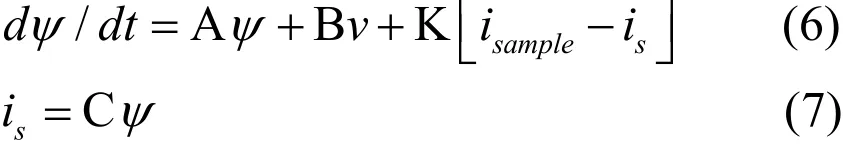
其中isample为电机真实输出电流，is为观测器输出的重构电流，在观测器最后一项是包括电机真实输出与观测器输出电流的修正项，增益矩阵K起到加权矩阵的作用，用于修正观测所得的定转子磁链状态变量。当观测器模型使用的矩阵A与实际系统的矩阵A之间存在差异时，必然导致观测器输出电流与电机实际输出电流之间存在偏差，在此情况下，该附加的修正项将进一步校正这些影响。其中，简化后的增益矩阵为：

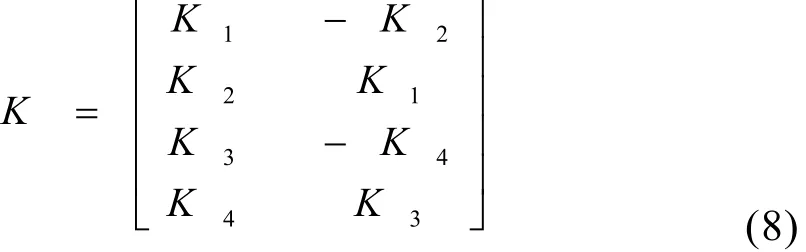
设定观测器的极点配置为电机极点的k倍[4]，则：

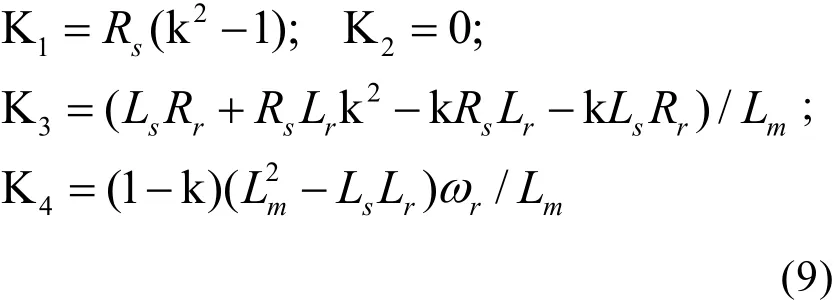
以上的增益矩阵具有普遍性，适合于任意型号的异步电机。另有简化的增益矩阵为：

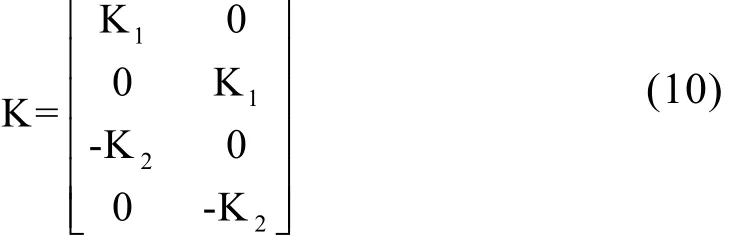
本试验中采用 K1=K2=0.125。其结构框图如图1。

3 速度辨识

通过简单的扩展，全阶观测器可以实现转子转速的在线辨识。把电机本身作为参考模型，全阶观测器作为可调模型，一般采用下式的比例积分形式的自适应率

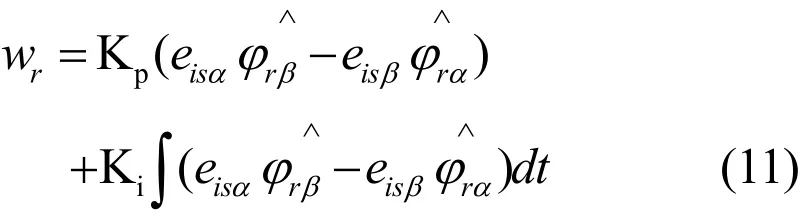
其中：

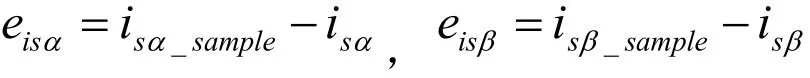
在上面的转子转速的估计方程中只包含可直接测量和观测的量，通过PI环节就可以实现转子转速的在线辨识[3]。

4 全阶磁链观测器离散化处理

上述全阶磁链观测器为四阶微分方程组，为了能够在数字信号处理器上实现对上述全阶磁链观测器的实时求解，必须将微分方程组转化为离散化形式，通常采用的离散化方法为数值积分法，本文在采用 TMS320F2407为控制芯片的控制系统中对一些常用的离散化方法[5]做了全阶磁链观测器的离散化处理，并分别做了试验验证。

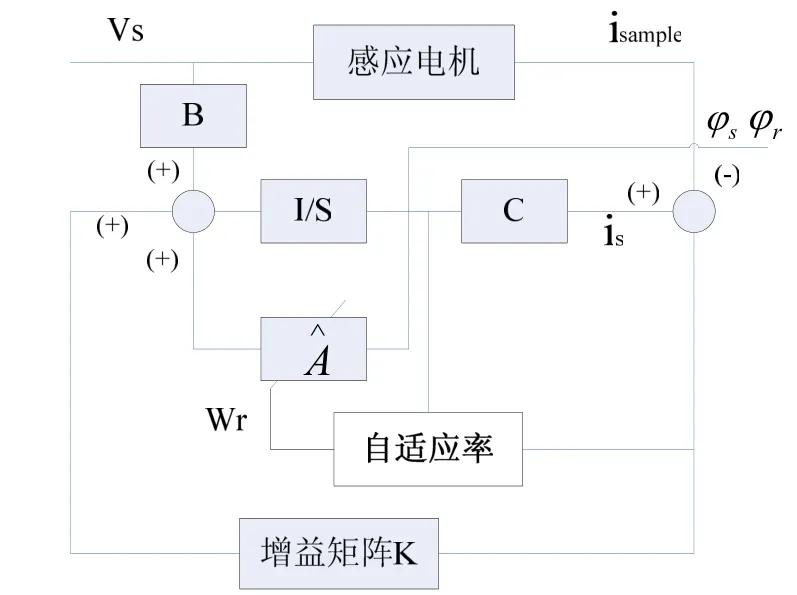
图1 全阶磁链观测器结构框图

显式欧拉法是最简单的离散化方法，系统中实现简单，但是在实际应用中控制系统的控制周期难以满足计算精度，导致控制效果很差，于是在离散化中采用改进欧拉法，即T形算法：先离散化计算得到预报值，然后利用隐形euler算法得到校正值，最后做算术平均，得到定转子磁链当前计算值。

采用T形算法后，离散化精度得到提高，为了进一步提高系统的控制效果，综合考虑离散精度和软件计算量，采用4阶runge_kutta显式离散算法对方程组进行离散化处理。

5 试验结果

根据以上的原理进行了一系列的试验，控制对象为300 kW异步电机，负载为300 kW交流自励同步发电机组，异步电机星形接法，额定电压为658 V，额定电流为304 A。

采用二阶 euler算法的磁链幅值控制结果如图2左，采用四阶runge_kutta算法的磁链幅值控制结果如图2右图，可以看出在采用四阶runge_kutta算法时候离散化精度更高，磁链控制效果更好。示波器采样异步电机额定工况时a相电流如图3所示。采用无速度传感器控制，在给定转速为1475 rpm时，采样转速与辨识转速如图4所示，辨识转速的精度在1%左右。

6 结论

对异步电机矢量控制中全阶磁链观测器进行了叙述，通过引入定子电流的反馈，使该观测器对参数的变化具有很强鲁棒性。对不同的离散化方法对全阶磁链观测器进行了离散化实现，并在实验中验证了全阶磁链观测器的鲁棒性和自适应能力。

图2 二阶euler算法转子磁链圆与四阶runge_kutta算法转子磁链圆

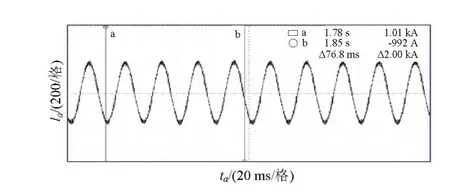
图3 额定工况异步电机a相电流波形

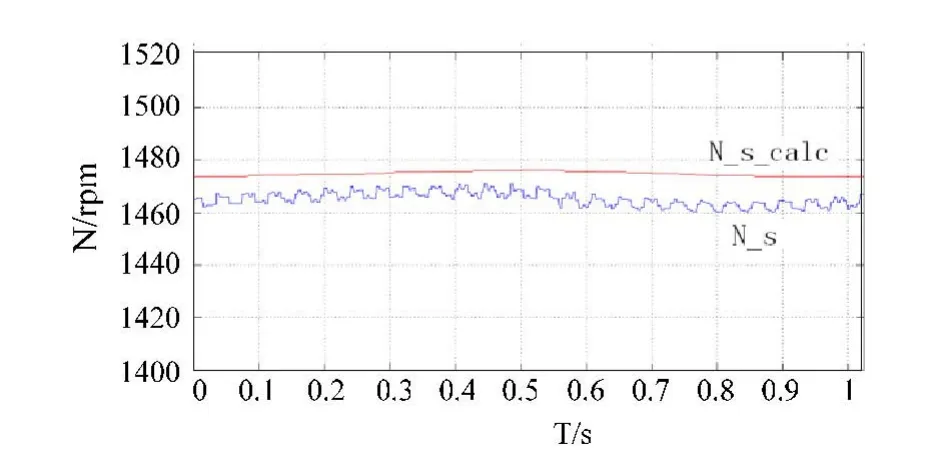
图4 辨识转速与测量转速波形

[1] 刘忠举, 梁宝明, 陈嘉福. 基于改进型积分器的矢量控制系统研究，电力电子技术, 2010, (2).

[2] 辜承林, 陈乔夫, 熊永前. 电机学. 华中科技大学出版社, 2003.

[3] 李磊.异步电机无速度传感器直接转矩控制系统的研究与实践[D]. 南京: 南京航空航天大学,2001.

[4] Hisao Kubota.New adaptive flux observer of induction meotor for wide speed range motor drives.IEC0N Proceedings(Industrial Electronics Conference)，Califom ia，1990，2：921～ 926.

[5] 李红. 数值分析. 武汉: 华中科技大学出版社,2003.