基于Simulink的直流伺服电机PID控制仿真
李沁生 于家凤
( 江苏海事职业技术学院轮机工程系,南京 211170 )
1 引言
轮机自动化中,无论是机械式,模拟式还是数字式控制器,普遍采用PID控制算法。PID控制参数整定的优劣直接决定着控制过程动态性能的好坏。通过计算机仿真来整定PID控制参数的传统方法要用到大量控制理论和计算机编程方面的知识,比较抽象,不易被轮机员所掌握。可视化编程环境为解决此类困难提供了便捷的手段。所谓可视化编程,指的是无须编写或只须编写很少的程序代码,随时可以看到运行结果,程序与结果的调整同步,这样能够极大提高工作效率[1]。
MATLAB是一个适用于科学计算和工程用的数学软件系统,历经多年的发展,已是科学与工程领域应用最广的软件工具[2]。该软件具有以下特点:数值计算功能强大;编程环简单;数据可视化功能强;丰富的程序工具箱;可扩展性能强等。Simulink是MATLAB下用于建立系统框图和仿真的环境。Simulink环境仿真的优点是:框图搭建方便、仿真参数可以随时修改、可实现完全可视化编程。
本文以工程控制中常用的直流伺服电机控制为例,演示了在Simulink环境下PID参数可视化整定及动态仿真的过程,为PID参数整定提供参考。
2 直流伺服电机模型[3]
2.1 直流伺服电机的物理模型
本文采用的直流伺服电机的物理模型与参数如图1所示。图中:ua—电枢输入电压(V);uq—感应电动势(V);ia— 电枢电流(A);Ra— 电枢电阻(Ω);La— 电枢电感(H);θ— 电机输出转角(rad);Tg—电机电磁转矩(N·m);J—转动惯量(kg·m2);B—粘性阻尼系数(N·m·s)
2.2 直流伺服电机的数学模型
2.2.1 基本方程组
根据基尔霍夫定律和牛顿第二定律对图1所示的电机列基本方程组:
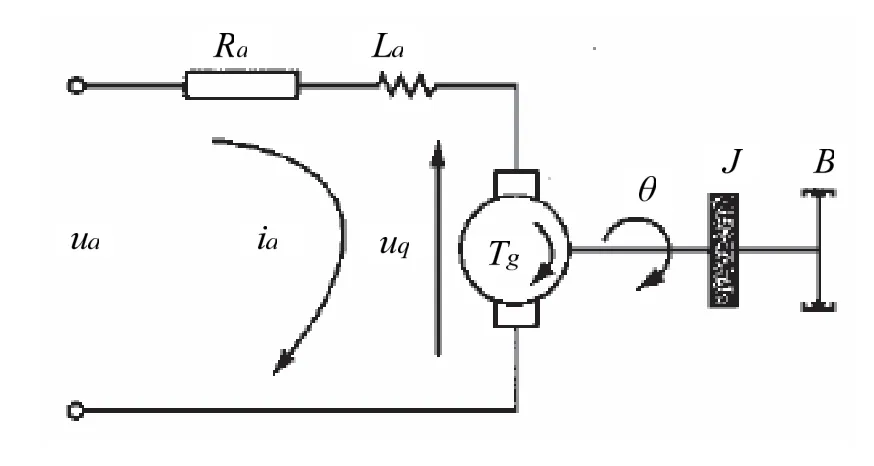
图1 直流伺服电机的物理模型
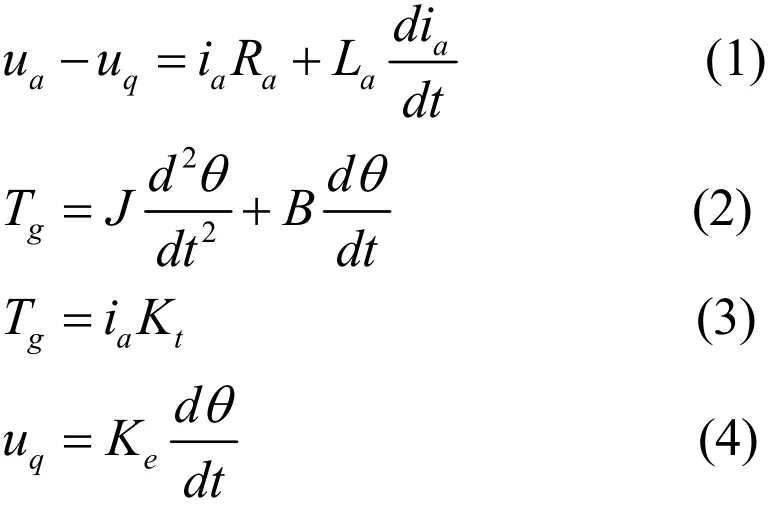
2.2.2 电机的传递函数
对式(1)—(4)进行拉普拉斯变换,得
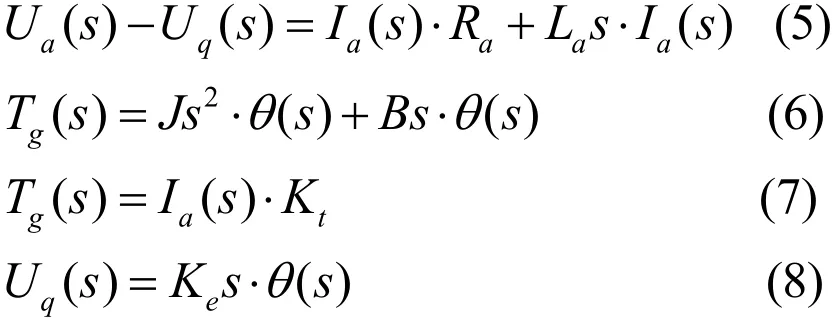
消去方程组的中间变量,整理得电机系统的传递函数
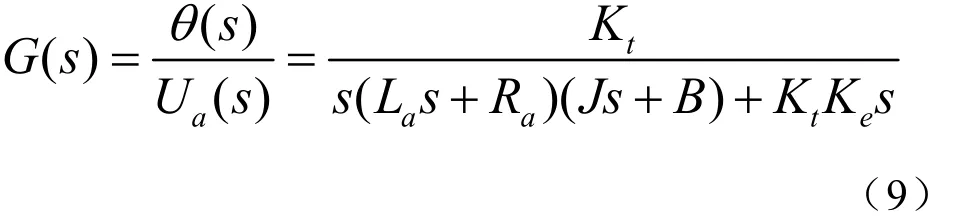
其中:J=3.23 mg·2m ,B=3.51µN·m·s,Ra=4 Ω,La=2.75 µH,K t=K e=0.03(N·m)A
3 PID控制简介[4]
PID控制是将设定值r(t)与输出反馈值C(t)的偏差e(t)=r(t)-C(t),按比例、积分、微分运算后,并通过线性组合构成控制量u(t),对控制对象进行控制,如图1所示,所以简称为P(比例)、I(积分)、D(微分)控制器。
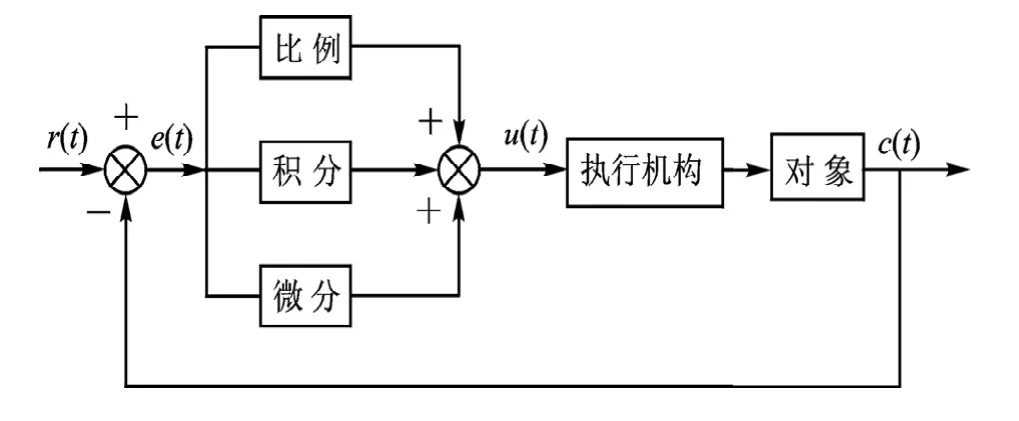
图2 PID 控制原理
(1)PID控制器的微分方程
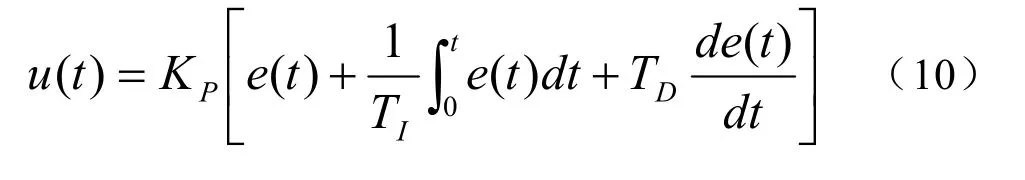
式中:Kp为比例系数,TI为积分时间,TD为微分时间
(2)PID控制器的传递函数
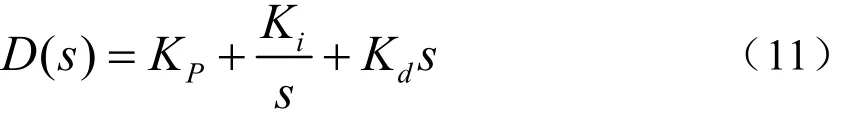
4 Simulink仿真
4.1 仿真系统的设计要求
本文所述电机系统(式(9))要求在电压输入端输入单位阶跃电压(1 V)后,直流伺服电机的转轴应能输出1 rad转角,且应同时满足下列要求:系统调整时间ts<0.04 s,最大超调量Mp<10﹪,系统稳态误差ess=0。
4.2 系统阶跃输入响应仿真
在Simulink中搭建图3所示方框图,设置仿真环境的参数。运行后显示如图4所示开环系统对单位阶跃输入的响应,即直流伺服电机输入单位阶跃电压时,电机的输出转角呈直线性上升。仿真结果表明,该系统没有达到预期的设计要求。

图3 开环系统阶跃输入响应方框图
4.3 PID校正
为了使系统能够达到设计要求,在图3的前向通道上设置一个PID控制器,基于Simulink构建如图5所示的闭环系统来校正直流伺服电机的转速。分别双击3个“Gain”元件,在其对话框里填入相应的Kp,Ki和Kd数值,即可构成P、PI、PID控制器.

图4 开环系统阶跃响应曲线
4.3.1 比例(P)控制校正
为使在要求的时间内达到设定的角位移,比例增益应尽可能大,以提高比例作用的强度,但必须同时考虑系统的稳定性。采用单纯的比例控制,其调整时间和超调量是一对矛盾,无法同时满足,要缩短调整时间,就要加大比例增益,但超调量也同时加大了。经过多次参数选择,当Kp=10、Ki=Kd=0时,运行后,得到图6,阶跃响应曲线较为理想,呈现接近75%衰减率的振荡过程。由图6可知0.04 s时的稳态误差为0.2044,超调量接近50%,均不能满足设计要求,特别是调节过程0.08 s后才能逐步进入稳态。
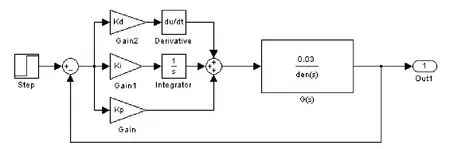
图5 PID校正系统阶跃输入响应方框图

图6 P校正系统阶跃响应曲线
由上述分析,对图6所示的动态过程,首先要采取措施缩短调整时间,减小超调量。
4.3.2 比例微分(PD)控制校正
微分作用具有超前控制能力,可抑制最大动态偏差,提高系统的稳定性。但微分作用又不能单独使用,因为它的输出仅与偏差的变化速度有关,如果偏差存在而不变化,微分作用是没有输出的。现将比例和微分控制结合使用,控制作用互补,组成PD控制器。令Kp=10,Kd=0.2,Ki=0,运行后,系统的阶跃响应曲线如图7所示,由图可知,此时动态过程的品质指标大幅度提高,其超调量、调整时间等均能满足设计要求,只是在调整时间范围内的稳态误差尚需进一步减小。由于加入微分了作用,系统的稳定性提高了,可适当增加比例增益,以减小稳态误差。令Kp=14,Kd=0.2,Ki=0,运行得到图8的响应曲线,和图7相比,在0.04 s时的稳态误差由0.0136减小到0.0029。
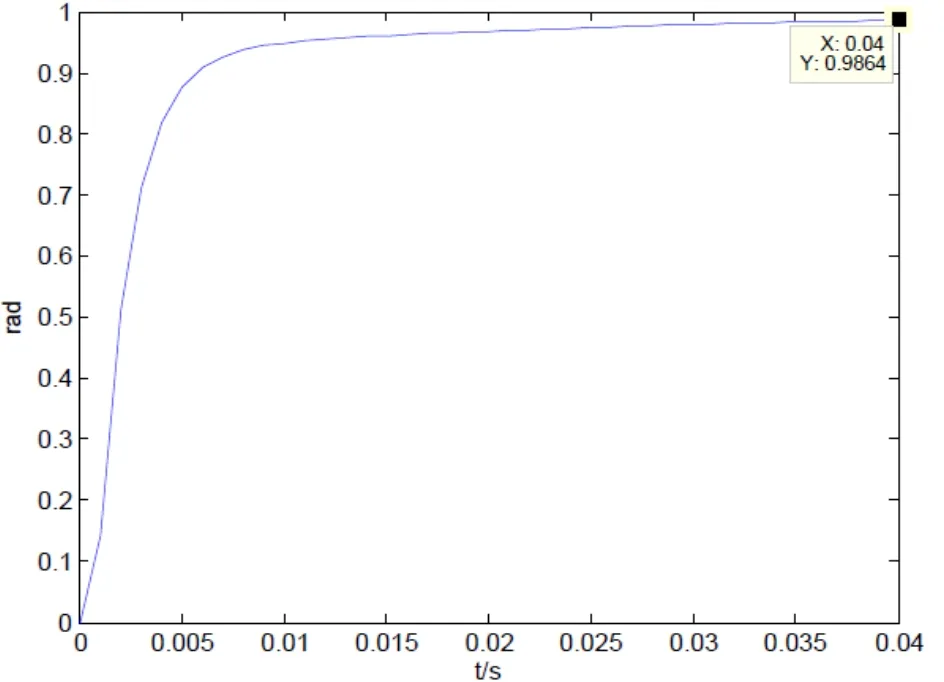
图7 PD校正系统阶跃响应曲线
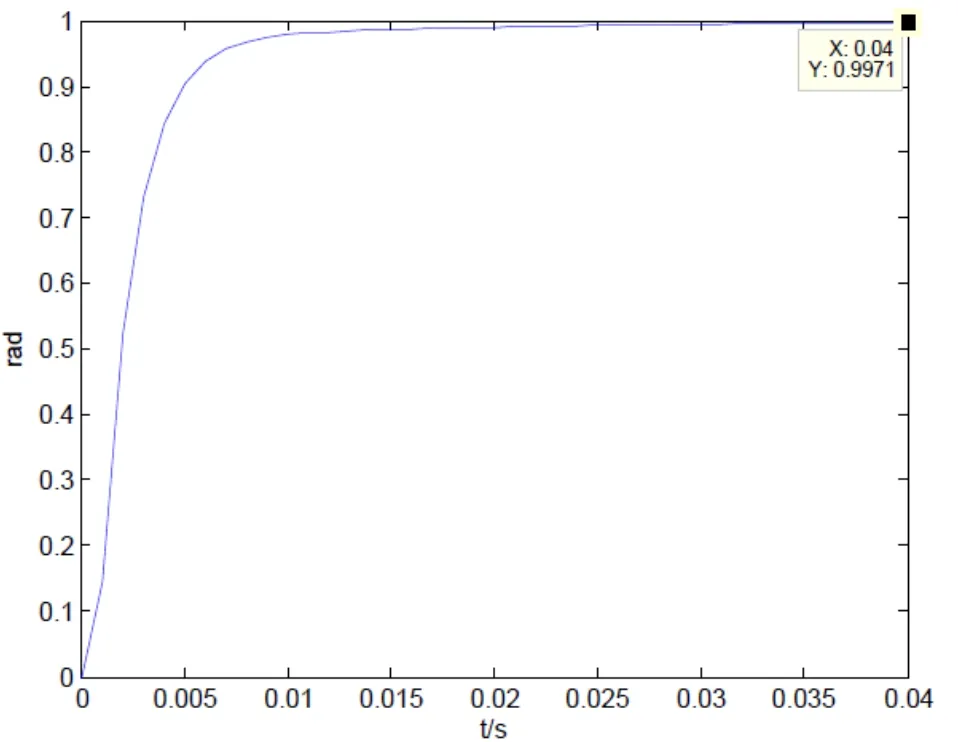
图8 改进比例系数后PD校正系统阶跃响应曲线
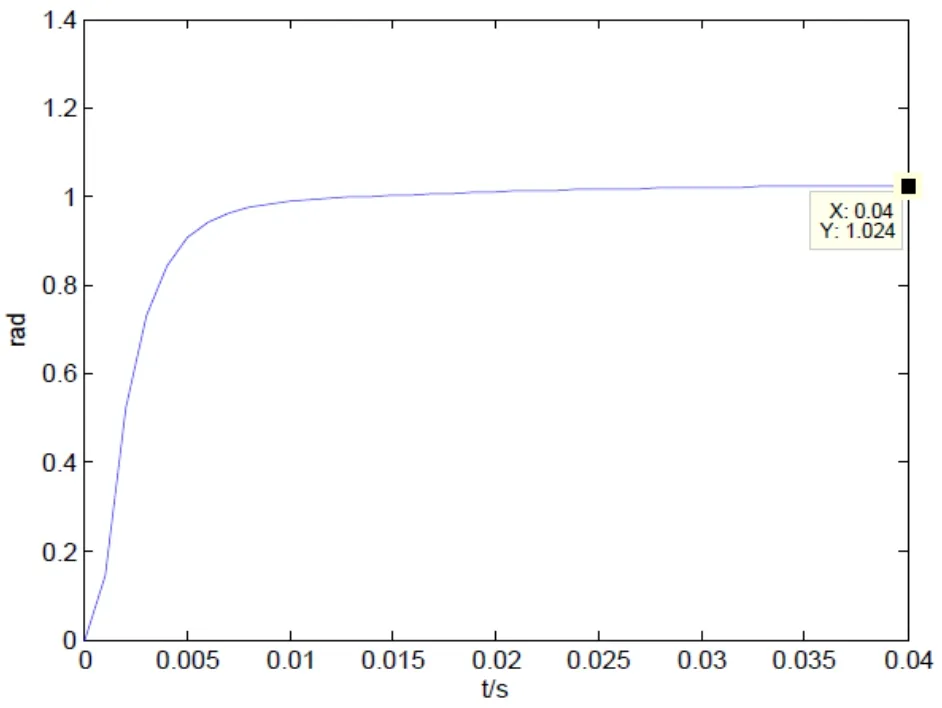
图9 PID校正系统阶跃响应曲线
3.3.3 PID控制器校正
从比例、微分作用的原理[5]可知,PD作用无法完全消除稳态误差,而积分作用主要用于消除静差[6]。为此,在PD作用的基础上加入积分作用,设Ki=200,以使稳态误差减至0。
运行得到如图9所示的阶跃响应曲线,由曲线可知其响应过程产生了超调,在0.04 s处的稳态误差为0.024,未达到设计要求。究其原因,是积分作用太强而产生了过调,考虑到此时其稳态误差已很小,稍有积分作用即可,于是令Ki=20,运行后得到图10所示的曲线,超调量为0%,在0.039 s处的稳态误差已为0,性能高于设计要求,稳定、准确、快速达到了完美的统一。
5 结论
通过上述实例的演示可知,在Simulink仿真环境下,建模简洁,修改参数方便,无须编写或只须编写很少的程序代码,就能准确、清晰地测绘出直流伺服电机对单位阶跃的输出响应曲线图,且有很高的量化精度。这种预见性,为系统PID控制规律的选择和参数整定提供了可视化而精确的依据。
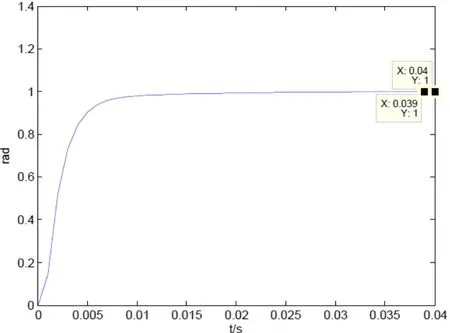
图10 满足要求的 PID校正系统阶跃响应曲线
[1] 庞中华,崔红. 系统辩识与自适应控制MATLAB仿真[M]. 北京:北京航空航天大学出版社,2009.
[2] 薛定宇. 控制系统计算机辅助设计-MATLAB语言及应用(第2版)[M]. 北京:清华大学出版社,2006.
[3] 白继平, 许德辉. 基于MATLAB下的PID控制仿真[J]. 中国航海,2004(4):77-80
[4] 陈平. 不完全微分型PID控制的应用研究[J]. 机电技术,2006(4):31-32
[5] 周晖. 基于MATLAB的PID参数整定[J]. 舰船电子对抗, 2008(4): 107-109
[6] 齐剑玲, 曾玉红, 刘慧芳. PID调节器的仿真研究[J].海淀走读大学学报, 2004(1): 69-71.

