基于常规遗传算法的混合电力滤波器优化配置

蒋海，栾桂海，杨光

(西南交通大学电气工程学院，四川 成都 610031)

1 引言

作为高压单相非线性负载的电气化铁道，是引起电力系统谐波污染的主要谐波源之一。中国现行的电力机车主要是交直型的大功率单相整流负荷，其特点是功率因数低，谐波含量多，其单相独立性又通过牵引变电所在系统中造成负序电流。因此，无功、谐波和负序的综合补偿成为交流牵引供电系统的重要技术课题。抑制网侧谐波电流的传统措施是在负荷端口装设无源电力滤波器(PPF)，它还可兼顾补偿无功功率，但无源电力滤波器存在相当多的缺陷。有源电力滤波器(APF)的最大特点是能对变化的谐波进行迅速的动态跟踪补偿，基本上克服了无源电力滤波器的缺点。但有源电力滤波器受其容量、开关元件的耐压和开关频率的限制，如果单独将它用于诸如电气化铁道牵引负荷这样的大容量谐波源的补偿，在工程实现的经济性和技术性上都存在相当的困难。因此，针对无源电力滤波器和有源电力滤波器各自的特点，充分发挥无源电力滤波器耐高压和大容量容易实现的特点，以及有源电力滤波器所具有的宽谐波抑制范围和自动跟踪优势，设计无源-有源混合型的电力滤波器将是一种投资适中、技术先进和性能优越的无功和谐波综合补偿方案。

新型的PHAPF结构，该混合电力滤波器将PPF和APF串联后再并联在母线上。这样APF能够改善PPF的滤波性能，防止PPF与系统阻抗发生谐振，而且通过控制使APF基本不承受基波电压，从而能大大降低APF的容量。APF串在PPF下部有利于保护和降低绝缘等级。其设计却需要考虑多种经济、技术和安全因素，是典型的多目标、非线性优化问题;若处理不当，极易造成滤波效果不佳、初期投资增加、系统无功补偿失当等不良后果。因此混合电力滤波器的容量优化是一个多目标的、有约束条件的非线性规划问题。利用常规遗传算法对其进行优化计算。

2 混合滤波器数学模型及算法

Fujita H等人提出的有源电力滤波器与无源滤波器串联后再与谐波源并联的混合型电力滤波器如图1所示。混合滤波器等值电路如图2所示。

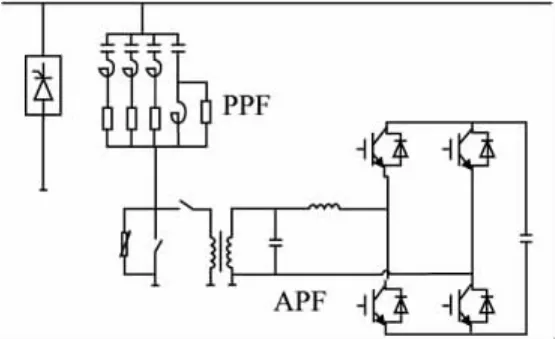
图1 混合型滤波器结构图

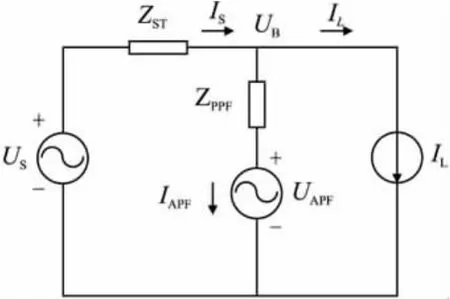
图2 混合电力滤波器等值电路

图中，US表示系统的等值电压;ZST表示系统及变压器阻抗，UB表示母线电压，ZPPF表示PPF的阻抗，uAPF、iAPF分别表示 APF的电压和电流，iS、iL分别表示系统和端口负荷电流。

2.1 无源电力滤波器容量计算模型

定义以下几个参数:

(1)无源滤波后的谐波残余度HRRn

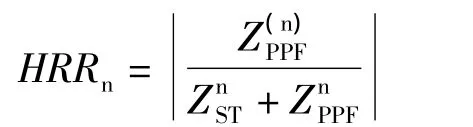
式中，n为谐波次数;是PPF第n次谐波的等值阻抗。

(2)单调谐滤波支路的调谐系数tn

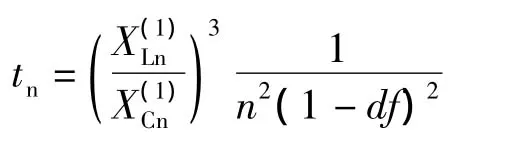
(3)PPF的滤波率dn

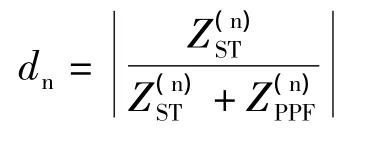
(4)无功补偿度KC

实际应用中，KC又由原功率因数cosφ0和补偿后的功率因数cosφC确定，即

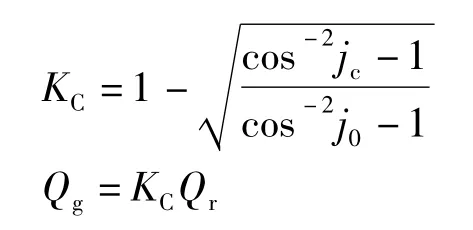
2.1.1 单调谐滤波器

对于固定的次边端口，n次单调谐滤波支路的m次谐波阻抗:

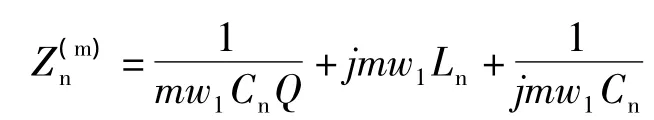
其中，Q为单调谐滤波支路的品质因数，n为3、5、7。

n次单调谐滤波支路电容器组以及串联电抗器容量分别是:

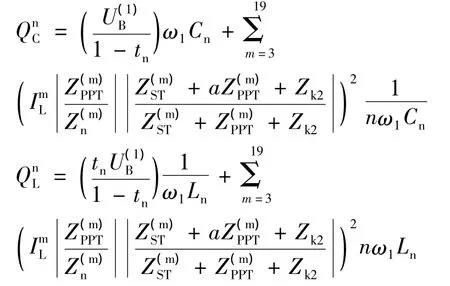
其中是母线基波电压，a为PPF滤除负荷中100a%的奇次谐波，Cn、Ln分别为n次单调谐滤波支路的电容和电感，Zk2是APF通过反馈控制呈现出的等效电阻。其中，

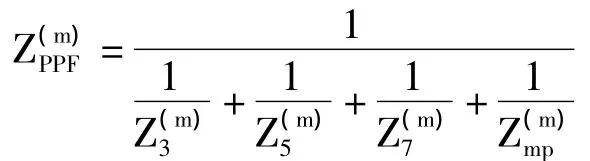
2.1.2 高通滤波器

高通滤波器的m次谐波阻抗

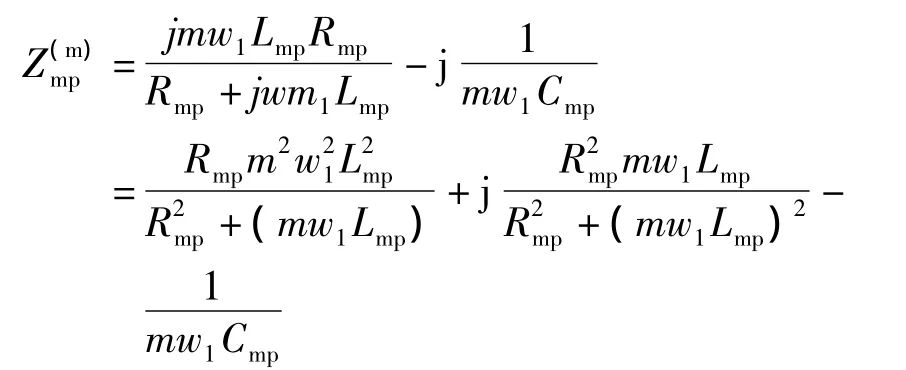
其中，Cmp、Lmp、Rmp分别是高通滤波器的电容、电感、电阻值。电阻和电感可用表示为:

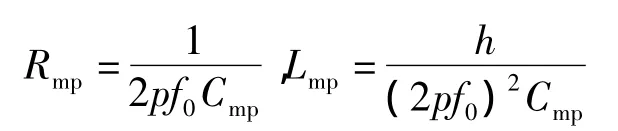
f0是截止频率。h是与品质因数直接相关的参数，一般在0.5～2之间。高通滤波器的电容器、电抗器、电阻的计算容量:

2.2 有源电力滤波器的容量计算模型

若要达到理想滤波效果，就有:

为了完成滤波任务，应有:

流过APF的总电流、总电压以及计算容量分别为:

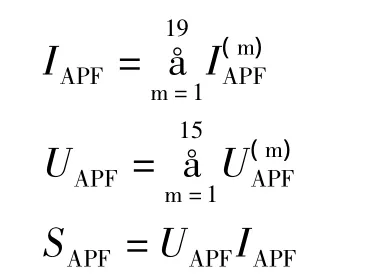
2.3 牵引变电所无功优化的数学模型

在满足一定的滤波率和各端口总基波无功补偿量不变的情况下，合理分配滤波支路的无功补偿，使得谐波含量最小，即滤波率足够的大，以及投资费用最少。其目标函数可以写成:

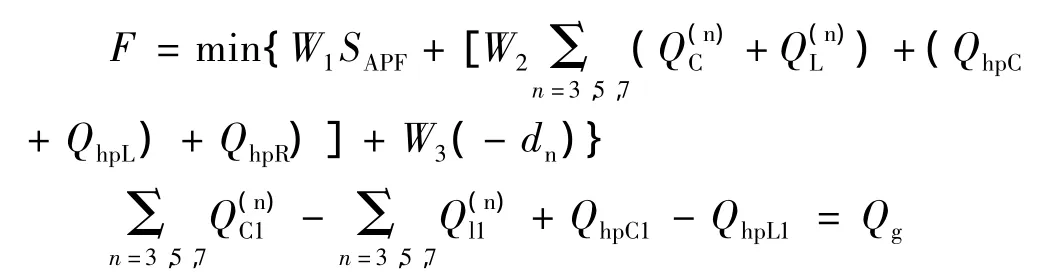
约束条件:

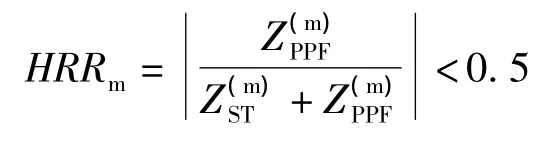
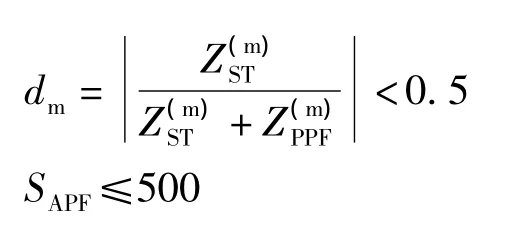
其中，m=(3，5，…19)，W1、W2表示有源电力滤波器和无源电力滤波器的投用加权系数，W3谐波滤波率不达标的惩罚因子。

目标函数是取最小值的问题，然而要求dn尽可能的大，所以在这里将取dn最大值的情况转化成最小值的情况，为了配合常规遗传算法，这里将dn变换成(-dn)，从而满足算法要求。

2.4 优化算法

遗传算法是一种模拟生物遗传、进化的机理，具有全局寻优能力的并行搜索算法;但经典的遗传算法(SGA)仅适用于单目标优化问题，且存在收敛概率低、速度慢、易早熟等缺陷［5］。对此，本文以可保证收敛性的最优保留遗传算法为基础，对种群规模、最大遗传代数、交叉率、变异率、基因长度以及有源电力滤波器和无源电力滤波器的投用加权系数，以及滤波率不达标的惩罚因子进行设置。

混合电力滤波器的容量优化是一个多目标的、有约束条件的非线性规划问题。利用MATLAB 7.1提供的遗传算法工具箱对其进行优化计算。

3 实际算例

本文以某牵引变电所的一个供电臂为对象，其实测供电臂95%最大电流如表1所示。

表1 牵引变电所供电臂95%概率最大电流(A)

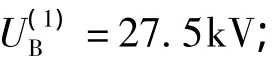
利用以上优化模型和优化算法进行计算，较优优化结果是当基因长度为5，种群规模为100，最大遗传代数为70，交叉率为0.85，变异率为0.001，滤波率不达标的惩罚因子为100，投资罚系数为20时取得。优化结果如表2所示。表3为加装滤波装置后的各次谐波电流。

4 结论

通过建立的混合滤波器数学模型，以混合滤波器的总容量最小为目标函数，兼顾滤波和无功补偿的需要，同时考虑到实际应用中的有源滤波器的容量不能太大、无源滤波支路的滤波率不能太低。

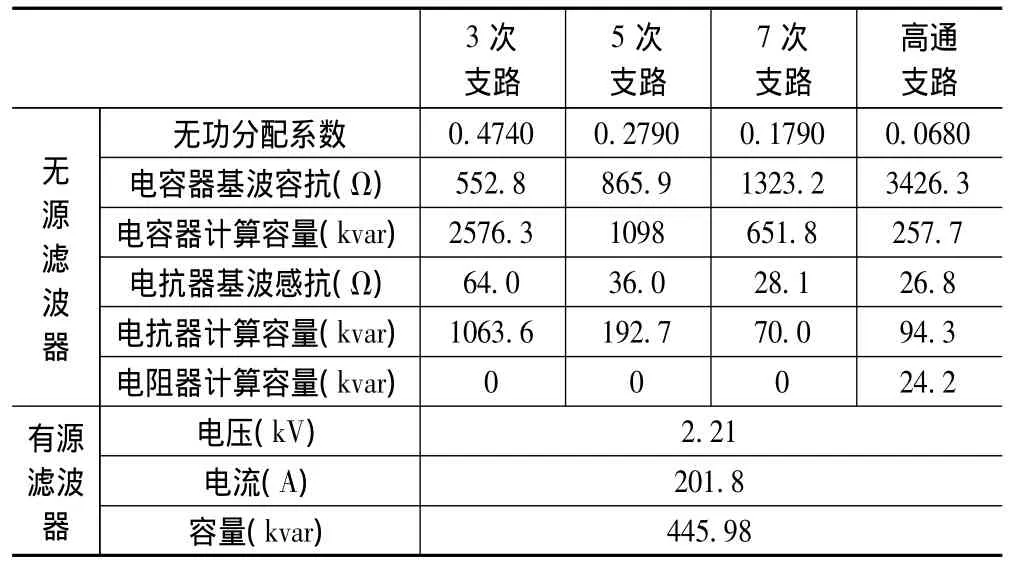
表2 混合滤波器容量优化结果

表3 加装滤波装置后的各次谐波电流

以某牵引变电所为例，分析、比较了混合滤波器方案、单独并联无源滤波器以及单独并联有源滤波器的方案，结果表明本文所采用的方案滤波效果明显，有效减少了混合滤波器的整体容量。并综合考虑混合滤波器设计的多种优化目标，将常规遗传算法有效的推广到了混合滤波器的容量优化计算中。利用基于常规遗传算法的优化计算方法，结果表明，该方法可获得兼顾多种预期目标的实用化设计结果。

［1］吴竟昌，孙树勤，宋文南，等.电力系统谐波［M］.北京水利电力出版社，1988.

［2］李群湛，贺建闽.电气化铁路电能质量及其综合控制技术［M］.西南交通大学出版社，2008.

［3］李群湛.关于IEC标准与电气化铁路谐波的思考.电能质量技术发展国际研讨会文集(上).

［4］李群湛.牵引变电所供电分析及综合补偿技术［M］.中国铁道出版社.

［5］陈国良，王熙法，庄镇泉等.遗传算法及其应用［M］.2版.北京:人民邮电出版社出版.

［6］雷英杰，张善文，等.MATLAB遗传算法工具箱及应用.西安电子科技大学出版社.

［7］李群湛.谐波影响分析与算法研究［J］.铁道学报(铁道牵引电气化与自动化专辑).1991.

［8］高明振，任震，唐卓尧，等.无源-有源混合滤波器容量优化设计［J］.铁道报，1999，21(5):43-46.