基于噪声检测的自适应中值滤波算法

时军艳， 刘树聃

(1.许昌市计算机信息技术应用研究所，河南许昌461000；2.许昌学院信息工程系，河南许昌461000)

0 引 言

在图像的编码及传输中，常常需要对图像进行椒盐噪声(即脉冲噪声)的滤除处理[1]。中值滤波因其与输入信号序列具有映射关系，在去除脉冲噪声上有比较好的效果，很多学者针对中值滤波技术进行研究，提出了很多改进算法。如加权中值滤波方法(WM)[2]，中心权值中值滤波器(CWM)[3]，三态中值滤波器(TSM)[4]模糊多极中值滤波方法[6]等，以及基于上述若干方法的改进策略[7]。文献[8]介绍了一种改进的自适应中值滤波方法(AM)，取得了不错的滤波效果，但其对于高密度噪声图像以及纹理细腻图像的边缘处理能力不佳[9]。本文将基于AM算法框架，通过分析图像噪声信息，提出一种新的基于噪声检测的自适应中值滤波，以克服对于高密度噪声及多细节图像去噪不理想的缺陷。实验结果表明，新算法对于细节丰富的图像以及高密度噪声的图像滤波效果良好，有效的提高图像的峰值信噪比，其去噪效果明显优于相比其他方法。

1 中值滤波法简介

早在1974年，Tukey提出了一维的中值滤波器，之后有学者成功将其扩展应用到二维图像。标准中值滤波(SM)采用滑动窗口划分出子图像，再对子图像进行二维中值滤波。滤波过程中，窗口大小可以设定为不同的值，一般是采用3*3的方形窗口。具体方法是对当前窗口内的像素点进行灰度值的排序，取中值作为当前像素点的灰度值。由于缺乏判断像素点是否有被噪声影响的机制，采用该方法时需对所有像素点进行一次滤波操作，在一定程度上会对图像的边缘细节信息造成破坏。

2 声点的检测

图像像素点受到椒盐噪声影响后，其灰度值表现为极大值或者极小值[9]。针对这一特性，在去噪处理之前，可以将像素点分成非噪声点、噪声点和图像细节点，以实现减少系统开销并保护非噪声点的目的。噪声点的检测通过全局检测和局部检测两个层次来判定，如下所述。

2.1 全局检测

在受椒盐噪声影响的图像中，噪声点的灰度值分布在图像灰度值的极大值端或者极小值端。若某点图像灰度值处在极值中间，则可以断定当前点未被噪声干扰，则无需去噪处理。而对于处于极值的像素点，还不能确定其是否是噪声点。

设图像灰度值中极大值为Gmax，极小值为Gmin，对于当前像素点灰度值G，若满足式(1)，则可以说明当前像素点并未受到噪声污染，无须进行滤波操作，其中T为设定的阈值

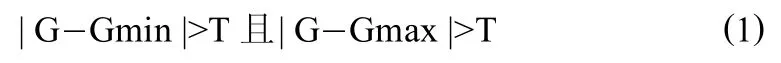
2.2 局部检测

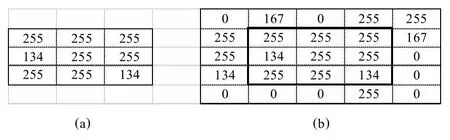
局部检测的目的是判别灰度值处于极值点像素点是否为噪声点。在图1中，分布着大量的黑白相间的条纹，即原图像素点中存在大量的极值。对于该种特点的图像，WM、CWM、TSM等大部分中值滤波方法由于将灰度值为极值的非噪声点误判为噪声点，导致处理结果都不是很理想。如何保证非噪声极值点不被滤波，或者滤波后不至于与周围差异较大的像素点进行错位，这需要充分结合像素点周围的信息进行分析。如图2所示，在3*3滤波窗口中，对于图(a)，因为窗口中心点灰度值与相邻点差值较大，噪声点的可能性较大；而对于图(b)，由于差值较小(为0)，非噪声点的可能性较大。

图1 存在大量极值的barb

图2 图像灰度值

2.3 噪声点检测算法

由上述分析，可归纳出完整的噪声点检测算法。

算法1：噪声点检测算法

输入：图像的全局极大值为Gmax，极小值为Gmin，滤波窗口最大值为Wmax，像素点P(a,b)及其灰度值G，阈值T。

输出：对像素点P(a,b)的判定。

(1)若满足|G-Gmin|>T 且|G-Gmax|>T，则转(6)；

(2)以P为中心，设置窗口大小w为3的滤波窗口；

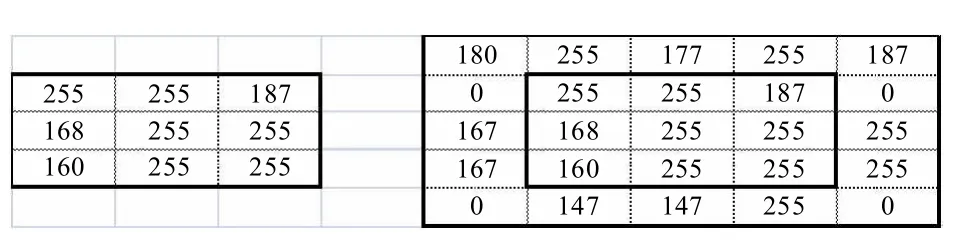
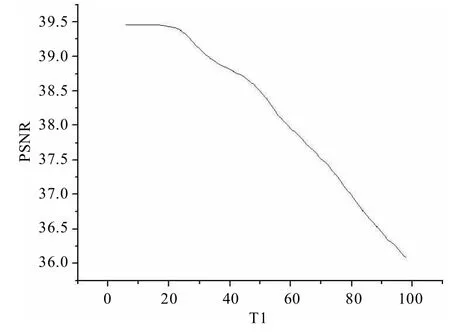
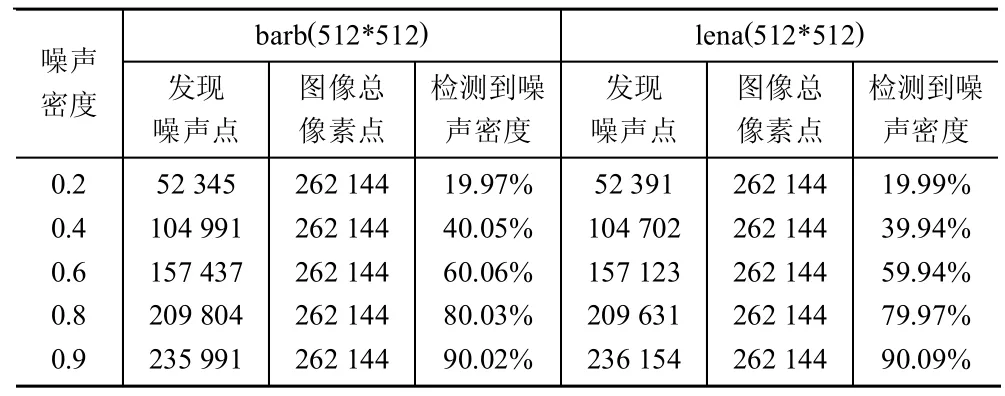
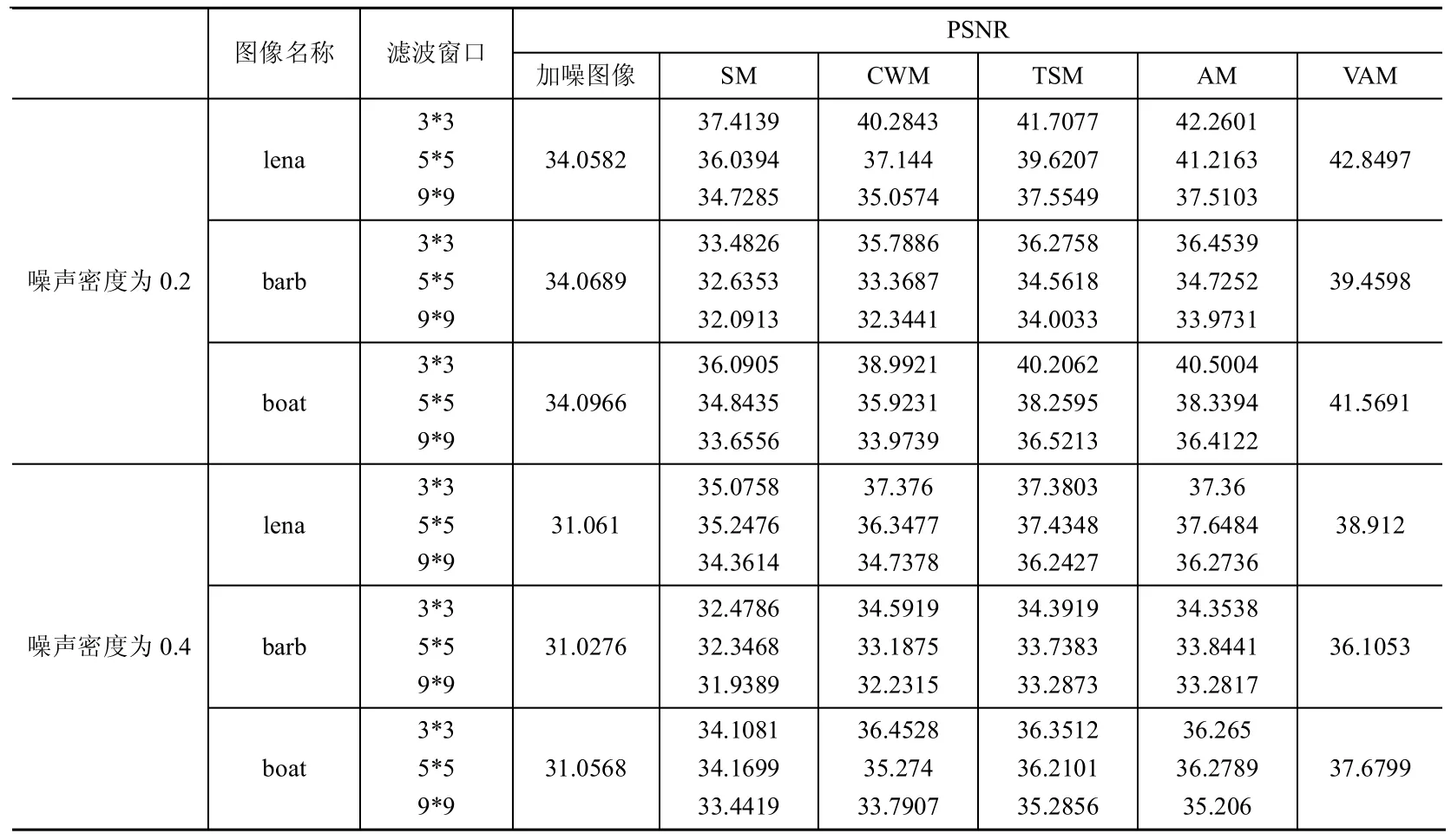
(3)计算该窗口内标准中值滤波结果，记为SM；若满足Gmin

(4)设置窗口大小扩展为w+2；若w>Wmax，则转到(5)，否则转到3；

(5)对于当前滤波窗口，计算像素点P与另外w*w-1个像素点灰度值差值的均值Gmean；若Gmean

(6)点P为非噪声点；

(7)点P为噪声点。

2.4 自适应窗口策略

在噪声点的检测过程中，滤波窗口的大小对滤波算法有非常大的影响：若窗口取值较小，能够有效的保护图像细节信息，但去噪效果相对较弱；反之，滤波器的去噪效果较强，而滤波后图像模糊程度则会加大。

图3表示的是噪声图像中某局部区域灰度值矩阵，当图像中噪声密度较大时，较小的窗口则无法保证Gmean正确表示出窗口中心值与边其他像素点的关系。如图(a)中，3*3窗口内含有6个噪声点，但极值都为极大值，因此窗口中心与其它8个像素点的差额均值仍为20左右，此时窗口中心被判断为非噪声点；而当窗口扩大后，噪声点虽然增加了，但极大值与极小值的比例发生变化，从而降低了噪声极值点对Gmean的影响，所求得的Gmean也正确的反映了窗口中心值为噪声点，在图(b)中可以看出，当采取5*5窗口时，Gmean经计算是大于T1的，可以判定窗口中心为噪声点。

图3 噪声密度为0.6的图像局部信息

对于滤波窗口大小的选取原则是使窗口内噪声点对Gmean的影响最小。此处采用标准中值滤波SM的值进行比较。若SM的值处于极大值与极小值之间，则可以说明极大值与极小值在该滤波窗口中的分布较均匀。

滤波窗口的自适应调整的作用不仅仅体现在噪声点判断上，对于噪声的滤除操作方面，窗口自适应也有着重要的作用，这一内容将在下文中详细说明。

3 噪声点的滤除

自适应窗口策略还可以更精确的区分噪声点与图像细节点，从而更好的保护了图像细节信息，并且能够更好的调整滤波器的去噪性能，有效的弥补了一般滤波器对于含有高密度噪声的图像处理上的不足。

图4展示了噪声密度0.2的lena图采用AM滤波器的去噪情况，可以看出，采用3*3窗口时一次滤波后噪声点无法完全滤除，而采用9*9窗口后，虽然噪声都已经滤除，但图像相对于原图有了较大的模糊。由此可知，窗口的大小对于滤波器去噪效果有重要的影响。当滤波窗口越小时，图像细节的保留越丰富，但去噪性能不佳；而当窗口增大时，去噪性能有了明显提升，但图像细节也随之被模糊。

当图像所含噪声密度较高时，窗口大小的影响更为明显。如图5所示，当噪声密度达到0.8时，该3*3窗口中经过SM的中值及其左右邻值全都为噪声点，此时进行任何滤波操作也不会改变其灰度值，滤波也失去其意义了。此时需要扩大窗口大小，以获取更多的图像信息来弥补噪声带来的影响。

图4 lena图采用AM滤波器的去噪效果

图5 噪声密度为0.8的图像局部灰度值

在噪声去除过程中，采用的窗口变化策略与噪声检测机制中介绍的自适应窗口策略基本一致，不同之处在于判断是否需要将窗口扩展时，采用AM进行判断。因为AM的输出值与窗口中值及其左右邻值相关，因此可以假定当AM滤波结果非极值时，此时的窗口大小即可作为去噪所用的窗口。经过分析可以发现，该种条件比噪声检测机制中的窗口变化条件更宽松：当SM值非极值时，AM值也非极值；但当SM值为极值时，由于AM是通过SM值与其左右邻值进行判定，AM值也极有可能不是极值[8]。因此采用这种判定方法有可能获得更小的窗口进行滤波。通过前文分析我们知道，较小的窗口，保留图像细节能力更强，因此采用该策略会达到更好的效果。

文献[8]介绍的AM噪声滤除算法所引入的线性自适应策略可以很好的去除噪声，但对于高密度噪声及细节丰富图像的处理效果相对于其它算法要差。而动态窗口策略则可以自适应选取合适的滤波窗口进行处理，有效的处理高密度噪声及细节丰富图像。在本文中针对此缺陷所设计的基于动态窗口的自适应中值滤波方法(VAM)即是对其的有效改进。

算法2：噪声点检测算法

输入：图像的全局极大值为Gmax，极小值为Gmin，滤波窗口最大值为Wmax，像素点P(a,b)及其灰度值G，阈值T。

输出：对像素点P(a,b)的判定。

(1)根据算法1，若点P为非噪声点，则结束，否则转(2)；

(2)以P为中心，设置窗口大小w为3的滤波窗口；

(3)计算当前滤波窗口下，采用AM滤算法的结果，记为AM；若满足 Gmin

(4)设置窗口大小扩展为w+2；若w>Wmax，则转到(5)，否则转到(3)；

(5)记当前AM为VAM，作为像素点P的滤波结果，并将VAM更新为像素点P滤波后的灰度值。

4 仿真结果以及分析

采用图例lena、barb进行仿真滤波比较。其中，lena的图像较为平缓，平坦区域多；而barb图则是细节信息非常丰富，难以处理。

4.1 噪声检测机制性能分析

对于2.1中提到的阈值T1取不同值，采用VAM滤波器对512*512的barb图进行滤波去噪，计算信噪比(PSNR)，绘制曲如图6所示。可以发现，T1的取值在10到20之间时，去噪效果最佳，当T1不断上升时，去噪效果随之递减。

图6 T1取不同值时VAM滤波所得的信噪比

在T1取值为15的情况下，分别对barb图像和lena图像加入一定密度的噪声，再进行噪声检测操作，统计其发现的噪声点数量以及发现的噪声密度如表1所示。可以看出，该噪声检测机制效果良好，检测结果与实际噪声密度误差较小。

表1 噪声检测机制所发现的噪声密度

4.2 VAM滤波器去噪效果分析

表2展示的是噪声密度为0.2和0.4时，lena，barb和boat这3幅图采用不同滤波算法的去噪结果。由图中可以看出，AM滤波器相对于其他算法有较好的改进，但对于纹理复杂的boat图所得到的结果要比其它算法偏差。而本文提出的VAM算法则对于各种特点不同图像都有较好的去噪效果，这是由于VAM在保留了AM处理平缓图像的优越性的同时，克服了AM在细节丰富时的不足，加强了图像细节的保留能力以及图像的去噪能力。

为了验证 VAM中自适应调整窗口策略比之于固定窗口策略在处理高密度噪声图像上的优势，图7展示了对于含80%噪声的lena图像处理情况。其中图7(b)、(c)、(d)分别是WM、TSM、AM以及AVM的滤波结果。可以看出，具有自适应调整窗口大小功能的VAM算法对于高密度噪声仍然有很强的处理能力，噪声可以准确滤除，并且图像细节及边缘信息保留良好。

表2 采用各类滤波方法对不同噪声密度下的不同图像滤波后的信噪比

图7 噪声密度为0.8的lena去噪结果

5 结束语

本文提出了一种基于噪声检测自适应中值滤波方法(AVM)。新算法采用合理的噪声检测机制，设计了窗口自适应调整策略，实现准确高效的区分噪声点与非噪声点，从而保护图像的细节边缘信息。经过实验仿真比较，本文所介绍的噪声滤波算法相对于其他典型算法，在噪声处理及细节保护上有明显的改进，对于高密度噪声的图像，则优势更加明显。

[1]陆天华.数字图像处理[M].北京:清华大学出版社,2007.

[2]Brownrigg D R K.The weighted median filter[J].Communications of the ACM,2007,27(8):807-818.

[3]Ko S J,Lee Y H.Center weighted median filters and their applications to image enhancement[J].IEEE Transactions on Circuits and Systems,2008,38(9):984-993.

[4]Tao Chen,Ma Kai-Kuang,Chen Li-Hui,et al.Median filter for image deonsing[J].IEEE Transactions on Image Processing,2007,8(12):1834-1838.

[5]Hwang H,Haddad R A.Adaptive median filters:new algorithm and results[J].IEEE Transaction on Image Processing,2006,4(4):499-502.

[6]YANG XH,TOH P S.Adaptive fuzzy multilevelmedian filter[J].IEEE Transaction on Image Processing,2008,4(5):680-682.

[7]ENG H L,MA K K.Noise adaptive soft-switching median filter[J].IEEE Transaction on Image Processing,2009,10(2):242-251.

[8]Chang Chin-Chen,Hsiao Ju-Yuan,Hsieh Chih-Ping.An adaptive median filter for image denoising[C].IEEE Second International Symposium on Intelligent Information Technology Application,2008:346-350.

[9]常瑞娜,穆晓敏,杨守义,等.基于中值的自适应均值滤波算法[J].计算机工程与设计,2008,29(16):4257-4259.