基于离散余弦变换的IMF特征频率提取

陈彦龙，张培林，吴定海，王怀光

(军械工程学院，石家庄 050003)

通过传感器提取的轴承振动加速度信号具有非线性、非平稳特征。经验模态分解(EMD)具有自适应的信号分解和降噪能力,非常适用于分析和处理非平稳、非线性信号，是轴承故障检测的一种有效途径，并得到了广泛应用[1-2]。

在EMD分解过程中，存在着很多影响分解结果的不确定因素，如插值误差、边界效应、终止筛选的标准不严格等，使各个固有模态函数(IMF)分量含有其他干扰成分，不能很好地表达IMF的物理意义，影响故障的准确判断[3]。

离散余弦变换(DCT)作为一种归一正交变换，在一定条件下是K-L变换的近似，且又有快速算法，在语音、图像的处理中得到广泛应用，研究表明该方法也能有效地应用于故障诊断[4]。文献[5]利用离散余弦变换对小波系数进行处理，实现了齿轮故障诊断；文献[6]利用离散分数余弦变换对信号进行降噪和识别，取得了良好的效果；文献[7]对高频段的小波系数采用离散余弦变换进行包络分析，提取出了列车的故障频率。

下文提出一种基于DCT的轴承IMF特征频率提取方法。首先对采样信号进行EMD处理得到IMF，利用DCT理论对IMF进行处理并重构信号，从重构信号中提取故障频率完成故障诊断。仿真信号和工程实际信号的处理结果表明，该方法能够突出受噪声污染的IMF中关键成分，明确物理意义，从而正确提取出特征频率，实现故障的可靠识别。

1 基于DCT的故障检测原理

1.1 IMF的计算方法

EMD方法中定义了IMF分量，1个IMF分量

必须满足下列2个条件：

(1) 在整个数据段内，极值点的个数和过零点的个数必须相等或相差1个；

(2) 在任意时刻，由局部极大值点形成的上包络线和由局部极小值点形成的下包络线的平均值为零。

对任一实信号x(t)进行EMD分解获得IMF的具体步骤是：

(1) 确定出信号x(t)上的所有极大值点和极小值点，然后将所有极大值点和所有极小值点分别用3次样条曲线连接起来,作为x(t)的上、下包络线,并计算出平均值曲线m1(t),再用x(t)减去m1(t)得

h1(t) =x(t)-m1(t) 。

(1)

如果h1(t)不满足IMF的条件，再将h1(t)作为原信号重复上述过程得到

h11(t) =h1(t)-m11(t) ，

(2)

并反复筛选k次，直到h1k(t)变为1个IMF，即

h1k(t) =h1(k-1)(t) -m1k(t) 。

(3)

这样,就从原信号中分解出了第1个IMF，称为第1阶IMF，并记作

c1(t) =h1k(t) 。

(4)

(2)从原信号中减去c1(t),得到第1阶剩余信号

r1(t)=x(t)-c1(t) ，

(5)

将r1(t)作为新的原信号重复步骤(1)，并对ri(t)进行同样的筛选，依次得到第2～n阶IMF和剩余信号，

r1(t)-c2(t)=r2(t)

⋮

rn-1(t)-cn(t)=rn(t)。

(6)

当剩余信号rn(t)变成一个单调函数，不能再从中提取IMF时筛选结束。

综上，可得到

(7)

至此，就将一个数据分解成若干IMF和残余量之和。严格意义上，IMF是满足单分量信号物理解释的一类信号，在每一时刻只有单一频率成分，从而使得瞬时频率具有了物理意义。直观上，IMF分量具有相同的极值点和过零点数目，其波形与标准正弦信号通过调幅和调频得到的新信号相似。但在EMD实际计算过程中，采用了近似处理，没有严格按照IMF的条件判别，不能完全保证IMF的物理意义，各个IMF分量中将出现其他干扰频率，造成故障误判。

1.2 离散余弦变换

一维离散余弦变换和反变换定义为

(8)

(9)

(10)

离散余弦变换具有良好的能量集中特性，这是其应用于信号检测的优点。离散余弦变换的1个变换系数对应一定的时长，通过检测各个时窗内信号幅值的变化捕捉信号的变化情况，而不是去捕捉与噪声统一数量级的信号突变，因此对噪声不敏感。这对轴承的在线状态检测与故障诊断非常实用[5]。同时，离散余弦变换属时频原子分解，其时频局部化特性和能量集中度好，是线性变换，无能量相干现象。离散余弦变换将信号的所有信息映像到多网格构成的时频平面，代表信号在时域、频域处的投影，分析系数变化就能检测到故障信号[7]。

为了突出IMF中的主要成分，将IMF进行DCT处理，对获得的DCT系数进行硬阈值处理，去除包含在正常信息中的噪声干扰，达到降噪和平滑的作用，突出故障特征，然后通过DCT逆变换重构信号，在重构信号中提取特征频率。

2 仿真信号分析

采用如下仿真信号进行试验分析, 采样频率1 000 Hz，时间长度2 s。

s=sin(40πt)+3sin(6πt)，

(11)

加入Gauss白噪声，时域波形图如图1所示。

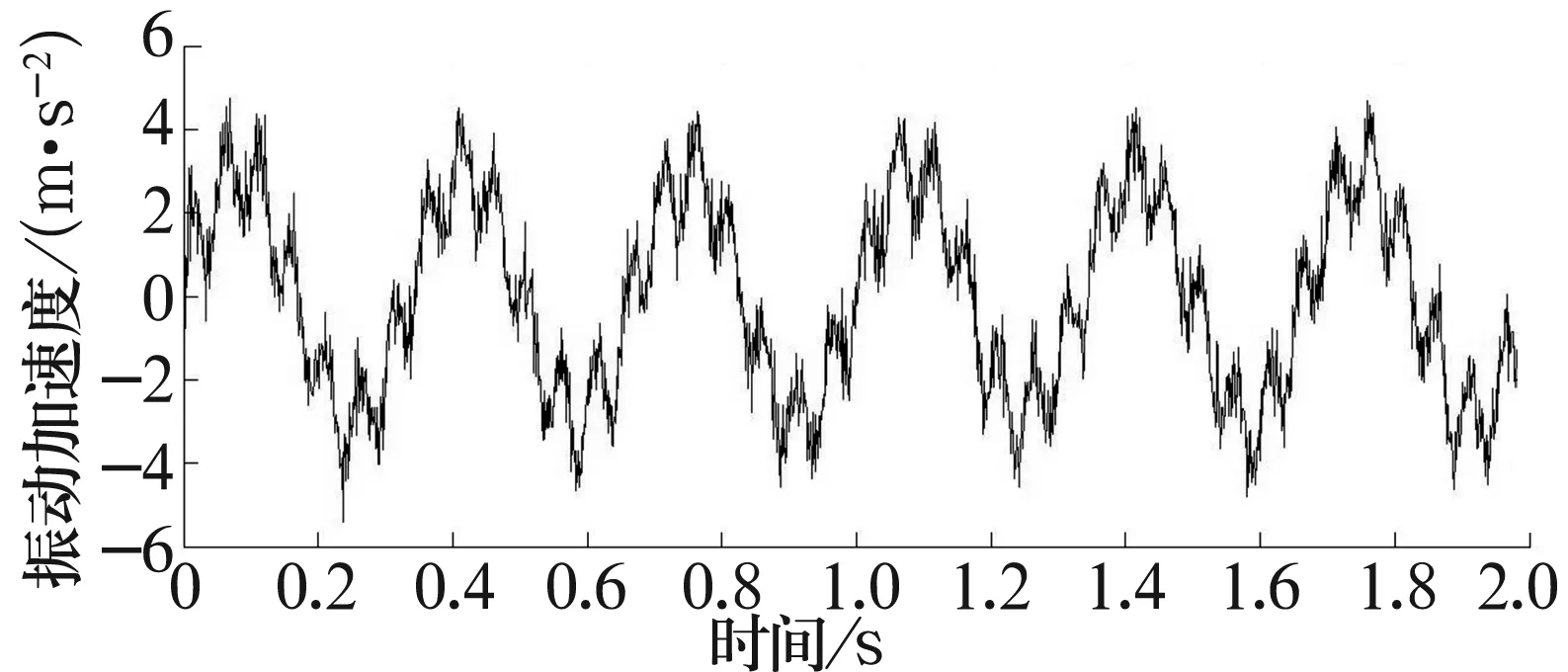
图1 仿真信号时域波形

将信号作EMD分析，选取其中一个IMF，如图2所示。该分量前后差异明显，后半部分幅值稳定，表现出周期性，前半部分含有高频成分，波形起伏较大，多次出现突变，成为不规则信号段，受到噪声污染。IMF具有明确的物理意义，直观上，其波形与一个标准正弦信号通过调幅和调频得到的新信号相似，该IMF并未表现出这一特征，给IMF的理解带来困难，这是分解过程中的不确定因素导致。

图2 IMF时域波形

图3为将IMF离散余弦分解，对分解系数进行硬阈值处理后，重构所得时域波形。对比图2，原始IMF信号高频噪声消失，突出了信号主要成分；信号突变消失，波形光滑、连续，具有明显的周期性；信号波形表现调制特征，表达了IMF应有的物理意义。

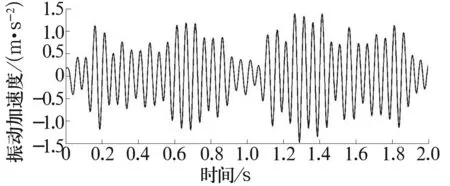
图3 DCT处理后IMF时域波形

对IMF在DCT处理前、后的信号进行频率分析，如图4所示。图4a中含有多余频率，说明信号受到其他成分的干扰，可能在工程实践中演变为较强烈干扰，影响故障判断。对信号进一步处理，图4b中干扰频率大量消失，几乎只保留故障特征频率。故障特征频率20 Hz对应仿真信号中sin(40πt)，具有明确的物理意义，结果准确。

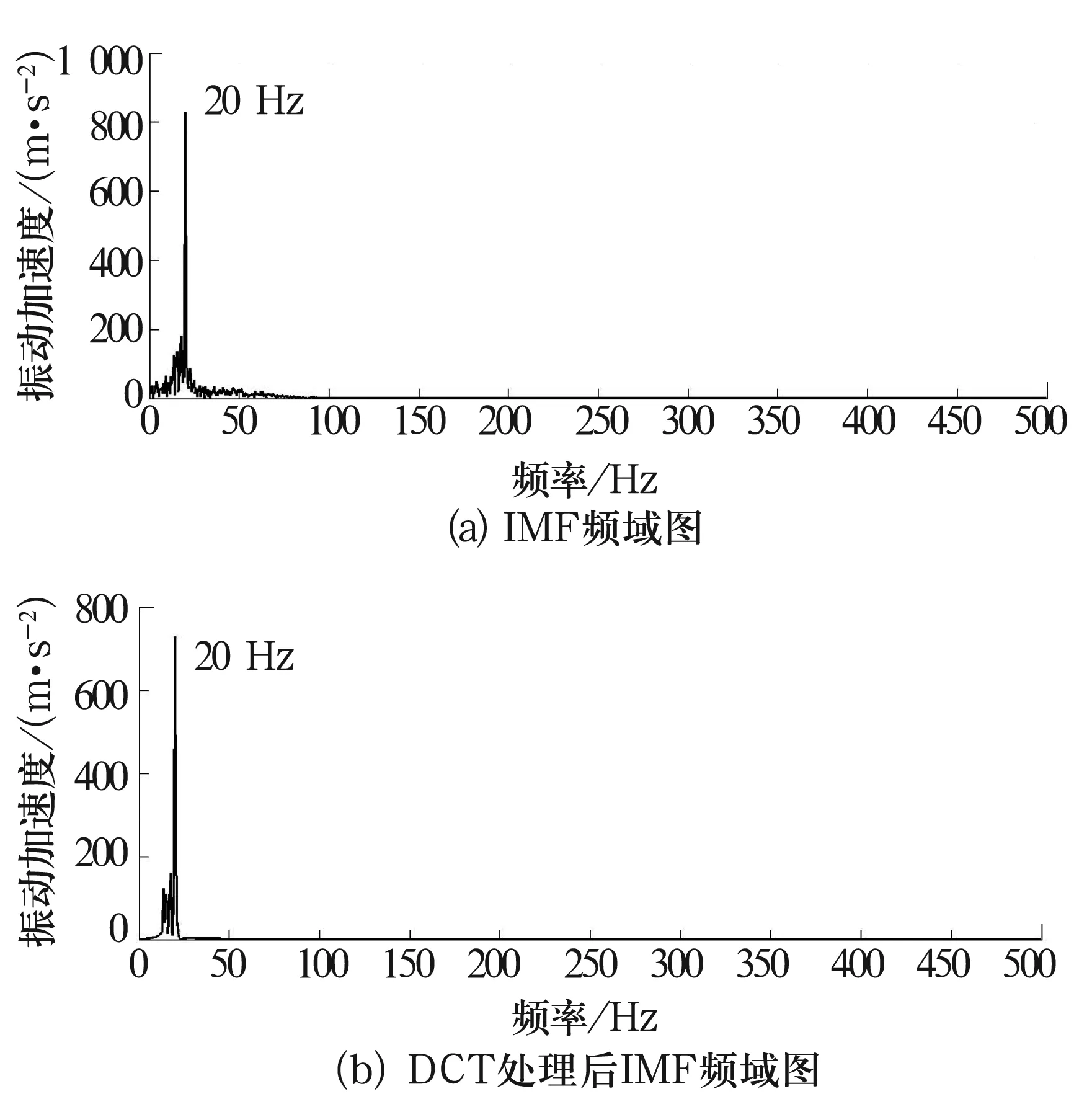
图4 IMF频域图对比

3 轴承故障信号分析

实测齿轮故障信号来自于单级传动的减速箱，轴承型号为6205-2RS JEM SKF, 故障设置为内圈单点故障，经计算得轴承内圈单点故障特征频率为158 Hz。转速为1 772 r/min, 振动加速度信号由安装在驱动端的加速度传感器进行采集,采样频率12 kHz，采样点数1 000。图5中故障信号淹没在振动信号中，无法直接识别。

图5 故障信号时域波形

图6为对信号EMD处理后所得IMF。信号随时间变化差异明显，前一部分波形变化较快，频率较高，最后一部分幅值不稳定，信号整体变化不规律。信号受到较强干扰，不能直观反映信号特征，有必要对信号进一步分析处理，凸显关键成分。

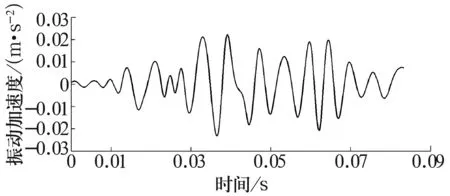
图6 IMF时域波形

对IMF进行DCT处理，重构得出如图7所示信号。直观上，其波形与标准正弦信号通过调幅得到的信号相似，严格符合IMF的数学要求，且与工程实践中轴承故障常受到调制这一现象符合。信号关键成分得到增强，反映出信号的主要特征；原始IMF中突变消失，波形光滑；信号具有明显周期性，利于EMD分解后的进一步分析。

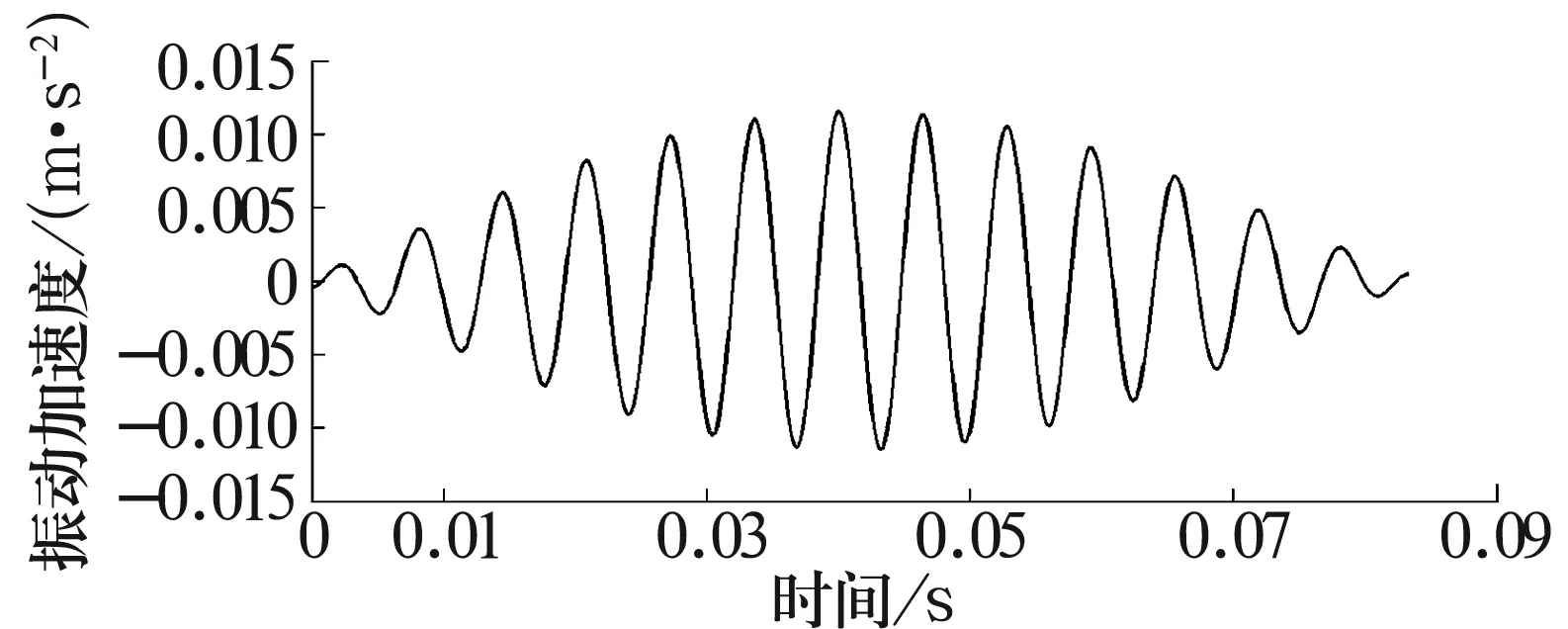
图7 DCT处理后IMF时域波形

对信号DCT处理前、后的IMF进行频率分析比较。图8a中频率上升和下降阶段均呈阶梯形，给信号的物理解释带来困难，故障诊断受到干扰，引起误判断。图8b为DCT处理后的重构信号频率图，图中仅出现了故障频率，干扰频率得到彻底清除，描绘了信号的主要成分。分析所得故障频率为156 Hz，与理论故障频率158 Hz相比，误差为1.28%，符合工程要求。

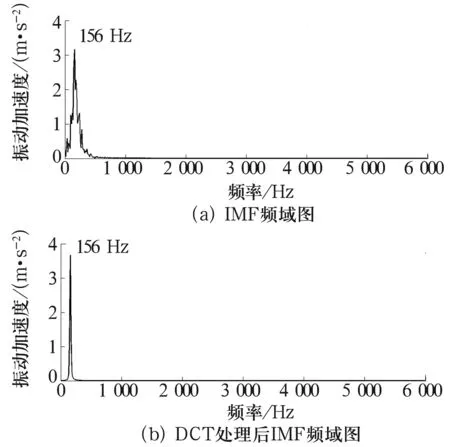
图8 IMF频域图对比

4 结束语

将IMF特征频率提取与离散余弦变换相结合，对仿真信号和实际信号进行分析， 取得了很好的效果。离散余弦变换具有快速算法，计算量小，算法简单，可以满足工程实时性要求。处理结果表明，该方法更精确地描述了IMF在时域和频域的特征，物理意义清晰，对于轴承故障诊断，是一种可靠而有效的办法。