磁悬浮轴承磁路结构分析与数学模型建立方法

何晓凤，邬清海

(淮阴工学院 电子与电气工程学院， 江苏 淮安 223003)

磁悬浮轴承是利用磁场力使转子无接触地悬浮并且悬浮位置可以由控制系统控制的一种新型轴承。磁悬浮轴承与传统轴承相比，具有无摩擦磨损、无需润滑、转速高、精度高和寿命长等诸多优点而被广泛地应用于机械工业、航空航天、机器人、计算机、能源交通及生命科学等领域[1]。分析磁路结构，建立悬浮力数学模型是设计性能优良磁悬浮轴承系统的关键。

1 磁轴承系统构成及其工作原理

一个完整的磁悬浮轴承系统由转子、电磁铁、控制器、功率放大器、带位移传感器的位移检测电路等部分组成[2-3]。图1所示为单自由度主动直流磁悬浮轴承差动控制系统构成和工作原理。该磁悬浮轴承系统由2个电磁铁控制1个自由度，电磁铁的偏磁电流为i0，假设转子受到扰动由平衡位置向下偏移很小的距离x0，传感器检测出x0，位置控制器将此位移变换成控制信号id，经功率放大器驱动得到电磁铁a的控制电流ic+=i0+id。由于控制电流增加，导致气隙磁通量增大，因而电磁铁a产生的磁吸力Fm+增大；同理，电磁铁b的控制电流ic-=i0-id，由于控制电流减小，气隙磁通量减小，因而电磁铁b产生的磁吸力Fm-减小，转子受到的合力Fres=Fm+-Fm-，方向向上，使转子回到平衡位置，此时电流id=0。同理，当转子向上偏移时，2个电磁铁会产生一个向下的合成悬浮吸力，使转子回到平衡位置。

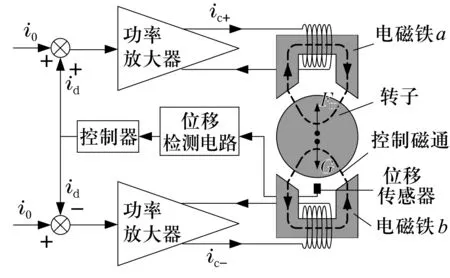
图1 磁悬浮轴承系统构成及工作原理示意图

2 磁悬浮轴承分类和特点

2.1 按控制电流性质分类

按照控制电流的性质，磁轴承可分为直流磁悬浮轴承和交流磁悬浮轴承。直流磁悬浮轴承采用直流功率放大器进行功率驱动，一个自由度上至少需要1个双极性直流功率放大器或2个单极性直流功率放大器。交流磁悬浮轴承采用交流功率逆变器进行功率驱动[4-5]。由于直流功率放大器价格高、体积大、功耗大，而交流功率逆变器技术成熟、价格便宜、功耗低，因此交流磁悬浮轴承可采用交流功率逆变器。

2.2 按受控自由度数分类

按照磁悬浮轴承对悬浮转子施加的受控自由度数可分为轴向单自由度磁悬浮轴承、径向二自由度磁悬浮轴承和径向-轴向三自由度磁悬浮轴承[3, 6]。轴向单自由度磁悬浮轴承主要实现转子在轴向上的稳定控制；径向二自由度磁悬浮轴承主要实现旋转主轴一端径向2个自由度的悬浮稳定控制；径向-轴向三自由度磁悬浮轴承集轴向单自由度磁悬浮轴承和径向二自由度磁悬浮轴承于一体，结构更加紧凑，且能同时实现旋转主轴一端径向2个自由度及轴向自由度的联合控制。将以上几种磁悬浮轴承进行不同组合可构成四自由度磁悬浮支承系统和五自由度磁悬浮支承系统。四自由度磁悬浮支承系统由2个径向二自由度磁悬浮轴承组成，五自由度磁悬浮支承系统由2个径向二自由度磁悬浮轴承加1个轴向单自由度磁悬浮轴承或1个径向二自由度磁悬浮轴承加1个径向-轴向三自由度磁悬浮轴承组成。

2.3 按悬浮力产生方式分类

按电磁力产生方式可分为主动磁悬浮轴承、被动磁悬浮轴承与混合磁悬浮轴承[1, 6]。

(1)主动磁悬浮轴承，也称电磁悬浮轴承，悬浮力全部由控制线圈产生，通过位移检测系统检测转子的位置，再由控制系统进行主动控制实现转子稳定悬浮。

(2)被动磁悬浮轴承，也称永磁悬浮轴承，悬浮力仅由永磁体或超导体产生，配以辅助机械装置实现对转子的支承控制。

(3)混合磁悬浮轴承，也称永磁和电磁混合的磁悬浮轴承，其机械结构包含了永磁体或超导体和控制线圈，永磁体或超导体用于提供静态偏磁磁通，当转子受到外界扰动或负载时，由控制线圈产生使转子回到平衡位置所需的控制磁通，其具备了被动磁悬浮轴承提供静态悬浮力和受到扰动时主动控制的优点。

2.4 按作用力方式分类

按照作用力可分为吸引式和排斥式，吸引式利用“异性相吸”的原理，排斥式利用“同性相斥”的原理。以德国为代表所设计的磁悬浮列车就是采用吸引式悬浮系统(EMS)，而以日本为代表的则采用排斥式悬浮系统(EDS)，世界第一条磁悬浮列车示范运营线——磁悬浮列车采用的是“常导磁吸型”，也属于吸引式。

2.5 按磁极布置形式分类

按照磁极布置形式，可分为同极磁悬浮轴承(Heteropolar Magnetic Bearing)和异极磁悬浮轴承(Homopolar Magnetic Bearing)[1]。同极磁悬浮轴承的磁通回路与转子的轴心线相垂直，而异极磁悬浮轴承的磁通回路与转子的轴心线相平行。同极磁悬浮轴承精度高、轴向尺寸较小、悬浮力较大、涡流损耗较小，缺点是磁滞损耗大；异极磁悬浮轴承的主要特点是转子始终在同一磁场极性下旋转，磁滞损耗小，缺点是轴向尺寸较大，空间利用率低。

2.6 其他分类

此外，还有按接触方式可分为完全非接触型和部分接触型；按结构可分为立式、卧式、内转子型和外转子型等。

3 磁路结构分析

3.1 单自由度磁悬浮轴承

图2a所示为单自由度主动磁悬浮轴承磁路结构示意图，由定子、吸力盘、控制线圈以及转轴等组成，由控制线圈产生的控制磁通在定子、吸力盘及其之间的气隙构成磁回路。控制线圈通电时，调节控制电流使电磁铁产生可控磁通，从而调整吸力盘左右磁吸力的大小，吸力盘在左右磁吸力作用下悬浮于中间平衡位置[7]。图2b所示为单自由度混合磁悬浮轴承磁路结构示意图[8]，其主要由定子、永磁体环、控制线圈、转子以及转轴构成。径向充磁永磁体环用于提供静态偏磁磁通，当没有外界扰动或负载时，转子仅在永磁体环的作用下稳定悬浮于平衡位置；当有扰动或负载时，调节控制线圈电流，产生控制磁通与永磁体环产生的静态偏磁磁通相叠加，产生用于承受扰动或负载所需的承载力。这种磁悬浮轴承结构仅靠永磁体产生偏置磁通，使控制线圈的安匝数大大减少，降低了功率放大器的功耗，缩小了磁悬浮轴承的体积，减轻了磁悬浮轴承的质量。

图2 单自由度磁悬浮轴承

3.2 径向二自由度磁悬浮轴承

图3a所示为直流径向二自由度主动异极磁悬浮轴承磁路结构示意图[6]，其结构为单片式六极结构，由带有6个磁极的定子、绕在每个磁极上的控制线圈、转子和转轴构成。每对磁极线圈通电后产生的磁通经定子、气隙和转子构成回路。图3b所示为直流径向二自由度混合异极磁悬浮轴承磁路结构示意图[9]，3块永磁体嵌于相隔的3个定子磁极中，另外3个磁极上则绕有控制线圈；每隔2个磁极采用1块隔磁铝块进行隔磁。永磁体产生的偏磁磁通和控制线圈产生的控制磁通均流经每对磁极与转子构成回路。

图3c所示为直流径向二自由度混合同极单片式四极磁悬浮轴承磁路结构示意图，由定子(4个磁极)、辅助定子、永磁体及叠片式转子组成。气隙处的控制磁通与永磁体提供的偏磁磁通在某一个方向叠加而在相反方向相减即可产生可控的悬浮力[9]。图3d所示为交流径向二自由度主动异极磁悬浮轴承[10]，3对磁极在空间沿圆周呈120°均匀分布，相对4对磁极的磁悬浮轴承简化了结构。3对磁极最大优点在于3组线圈可通过1个三相功率逆变器提供三相交流励磁控制电流产生一个合成旋转磁场，通过电流与位移反馈式的闭环控制方法，合成磁通则可指向与转子位置偏移相反的方向，从而可产生使转子回到平衡位置的径向悬浮力，支承转子于平衡位置，可大幅度降低磁悬浮轴承功放成本及体积。

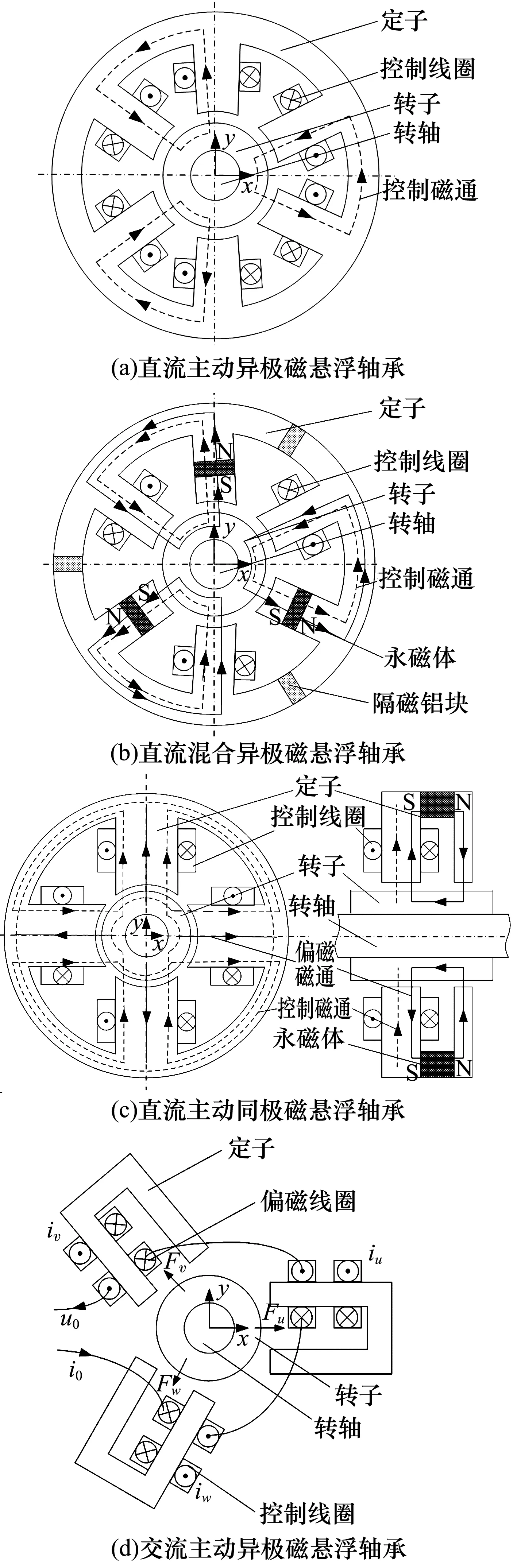
图3 径向二自由度磁悬浮轴承

3.3 径向-轴向三自由度磁悬浮轴承

图4a所示为直流径向-轴向三自由度混合磁悬浮轴承[11]，由轴向定子、轴向控制线圈、径向定子、径向控制线圈、环形永磁体、转子及转轴等构成。环形永磁体同时提供轴向、径向偏置磁通，轴向2个线圈、径向分别对置的2个线圈串联作为相关自由度的控制线圈。该结构具有结构紧凑、承载力大等特点；但需要3路双极性直流功率放大电路，其功率损耗较大。

图4b所示为交直流径向-轴向三自由度混合磁悬浮轴承磁路结构示意图[6]，其轴向采用直流开关功放驱动，径向采用1个三相逆变器进行驱动，由径向充磁的环形永磁体同时给轴向和径向提供静态偏磁磁通。这种交直流三自由度混合磁悬浮轴承集三相交流驱动、永磁偏置及轴向-径向联合控制等优点于一体，减少了磁悬浮轴承系统的体积，大大降低了功率放大器的损耗，具有效率高、成本低等特点。

图4c所示为径向-轴向三自由度锥形滚柱式磁悬浮轴承结构，转子在轴承范围内做成圆锥形，垂直于圆锥面的磁通产生的磁力可分解为轴向与径向悬浮力，从而可控制轴向和径向自由度。由于其各自由度之间存在相互耦合，增加了控制难度。且系统抗干扰性能差，另外采用直流驱动，功放体积大、功耗大、成本高[12]。

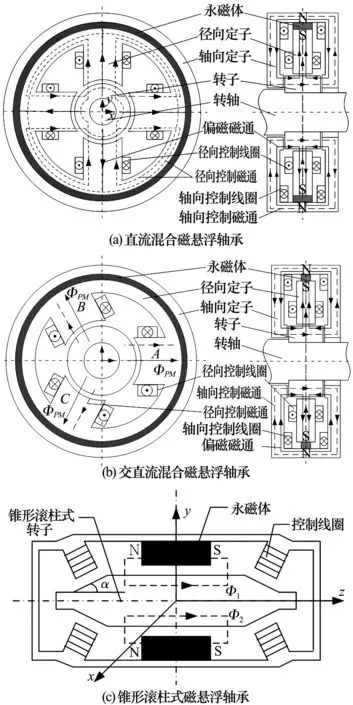
图4 径向-轴向三自由度磁悬浮轴承

综上所述，要设计出性能更加优良的磁悬浮轴承系统应主要从以下几个方面进行研究。

(1)采用永磁体提供静态偏磁磁通的混合磁悬浮轴承体积较小，承载能力较大，当磁悬浮轴承系统无负载或外界扰动时，磁悬浮轴承完全依靠永磁体就能实现稳定悬浮；加之我国用于制造永磁体的稀土资源丰富，因而永磁偏磁混合磁悬浮轴承将会是今后很长一段时间的研究热点。

(2)交流磁悬浮轴承采用交流功率逆变器驱动控制线圈，1个交流功率逆变器就可以完全驱动径向2个自由度，相比于传统的直流磁悬浮轴承，其功率损耗大大降低，能够有效降低磁悬浮轴承系统成本，因而交流磁悬浮轴承将会越来越多地受到国内、外磁悬浮轴承研究人员的关注。

(3)集轴向、径向于一体的三自由度混合磁悬浮轴承相比于传统的1个径向二自由度磁悬浮轴承和1个轴向单自由度混合磁悬浮轴承而言，其结构更加紧凑，并将大大减小磁悬浮轴承的体积，这势必成为未来磁悬浮轴承研究的一个重要方向。

(4)在一些特殊领域需要使磁悬浮轴承外部旋转，这就使得有必要对外转子磁悬浮轴承进行研究，外转子磁悬浮轴承的磁路结构设计将会是一个十分重要的研究方向，随着该项技术的研究将把磁悬浮轴承技术拓展到更多的应用领域。

4 建立数学模型

目前建立磁悬浮轴承悬浮力数学模型的方法大多采用等效磁路法，等效磁路法的基本思想是：用电阻代替表示各气隙处的磁导以及铁芯磁阻，用电场表示各线圈产生的磁场和永磁体产生的磁场。由于磁悬浮轴承定子、转子铁芯都是由高导磁材料制成，具有磁饱和及磁滞等现象，要对磁悬浮轴承的磁场进行精确的数学分析十分困难。考虑到有些因素对系统模型的影响比较小，所以在建立数学模型之前，为了使问题简化，应集中考虑主要因素，只需考虑工作气隙的磁阻，忽略磁悬浮轴承的定、转子铁芯磁阻、磁滞、涡流损耗及漏磁等[4-9]。采用等效磁路法建立磁悬浮轴承悬浮力数学模型的主要步骤为：

(1)根据磁悬浮轴承产生的磁回路，采用等效磁路法得到其等效磁路图；

(2)根据等效磁路图求出各悬浮气隙处的气隙磁导G；

(3)根据磁路基尔霍夫定律∑F=0和∑Φi=0，求解出各支路的磁通Φ；

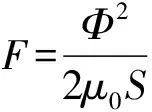
下文采用等效磁路法建立图4b所示交直流径向-轴向三自由度混合磁悬浮轴承轴向悬浮力的数学模型。交直流径向-轴向三自由度混合磁悬浮轴承等效磁路图如图5所示。图中Fm为永磁体对外提供的磁动势；Φm为永磁体发出的总磁通；Gz-和Gz+分别为左、右轴向气隙磁导；GA，GB和GC为径向3个气隙磁导；Nziz为轴向控制线圈安匝数；NAiA，NBiB和NCiC为径向控制线圈安匝数。

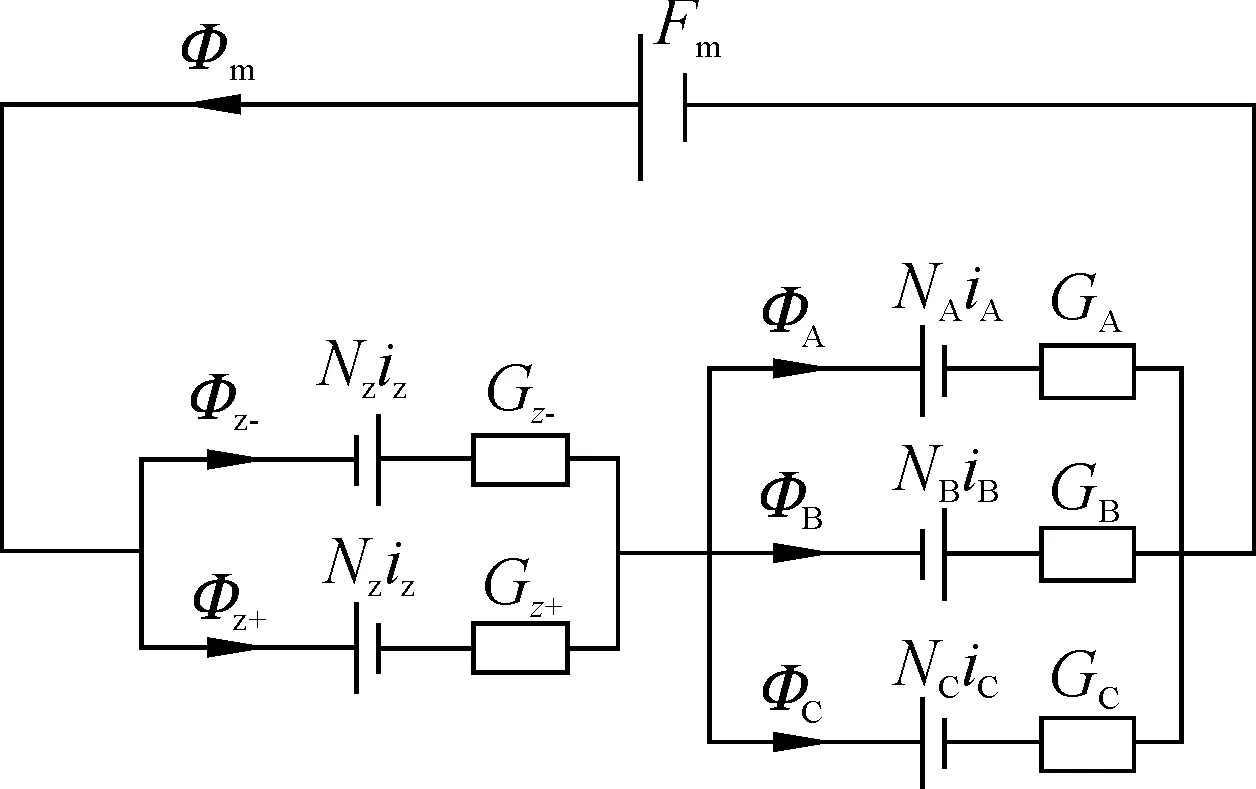
图5 交直流径向-轴向三自由度混合磁悬浮轴承

现假设转子轴向向左偏移z，则轴向左、右气隙处的磁导为

(1)

式中：μ0为真空磁导率；Sz为轴向单个磁极面积；δz为轴向气隙长度。所以左、右轴向气隙磁通为

(2)

则交直流径向-轴向三自由度混合磁悬浮轴承轴向合成悬浮力为

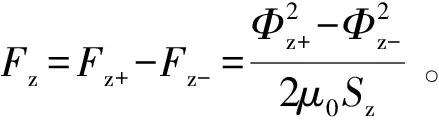
(3)

5 结束语

通过对比分析了各种磁悬浮轴承的磁路结构和特点，展望了磁悬浮轴承重点研究方向，阐述了基于等效磁路法的磁悬浮轴承悬浮力数学模型建立方法，为磁悬浮轴承的磁路结构设计及其控制系统的研究提供了参考。