基于混合型多结点样条插值曲面的图像放大方法*

蔡占川,郑才目, 黄 静, 梁延研

(1. 澳门科技大学资讯科技学院,澳门；2. 北京师范大学珠海分校信息技术学院, 广东 珠海 519085)

1975年齐东旭[8]给出了多结点样条基本函数的构造及计算格式，后续文献[9-10]对其作进一步的理论分析和应用。为了兼顾插值与逼近方法的优点，多结点样条函数在通常的样条函数中引入更多的附加结点，通过增加结点带来的自由度来构造原结点上插值的高精度样条逼近格式。多结点样条基函数是基数型的，使得插值过程无须求解方程组，同时，多结点样条基函数具有有界支集，保证了局部性和有效性。多结点样条以其良好的局部性、插值性等优越性，已被成功地应用于飞机外形、机翼、海洋、地质的数据处理以及动画片的计算机制作等领域[11-13]。

本文首先介绍混合型多结点样条函数；其次，由数字图像构造混合型多结点样条插值曲面，提出一种利用混合型多结点样条插值曲面的图像放大方法；同时为了提高该方法的效率，描述了一种加速算法；最后是实验结果与结论。

1 混合型多结点样条

1.1 混合型多结点样条函数

多结点样条曲线是建立在样条理论基础上的一种插值曲线，文献[8-10]对其性质进行了充分讨论。多结点样条是通过对等距样条基函数的平移和迭加变换而得到的，它不仅能对插值点点点通过，并且保持了曲线样条的局部性、显式表达和容易交互的性质。

这里讨论另一类多结点样条基本函数，记为pk(x)，它与一般基本函数Ωk(x)具有相同的跨度(-ξk,ξk)，ξk=(k+1)/2，k∈Z[8]。用基本样条函数的组合形成多结点样条基本函数，令

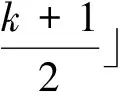
p3(x)=-3Ω3(x)+4Ω2(x)

基函数图形如图1所示。

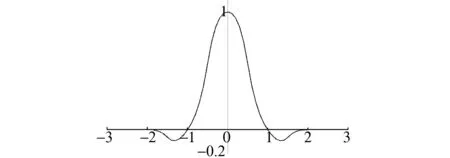
图1 混合型多结点样条基函数

1.2 混合型多结点样条插值曲面

一般地，混合型多结点样条的插值函数可写为

2.2.1 气切吸痰 吸痰是清理呼吸道、保持呼吸道通畅的最常用而重要的护理操作[2]，也是无菌操作技术，操作时戴一次性无菌手套，并使用一次性无菌吸痰管，或者密闭式吸痰管。操作前后注意医护人员的手卫生，吸痰前听诊患者肺部是否有痰鸣音，观察患者表现：有无烦躁、呼吸困难或血氧饱和度降低等情况或呼吸机报警为气道压力过高时，需及时吸痰。吸痰操作时动作轻柔，吸痰中注意：插入吸痰管时阻断负压，防止损伤的气管黏膜，使其充血、水肿、上皮组织脱落、纤毛的丢失，以及气道内肉芽肿的形成，否则会增加了患者气道黏膜的出血和感染的机会[3]；吸痰前后给予纯氧吸入，防止供氧不足或吸痰后肺不张引起患者低氧血症。

(4)

其中f(xi)(i=0,1,…,n)是采样值；pk为混合型多结点样条。

相应地，混合型多结点曲面插值公式为

0≤u≤m,0≤v≤n

(5)

其中pk为u方向上的混合型多结点样条基函数，pl为v方向上的混合型多结点样条基函数，Pij为控制顶点，根据上式可以张成k×l阶混合型多结点样条曲面。

2 由数字图像构造混合型多结点样条插值曲面算法

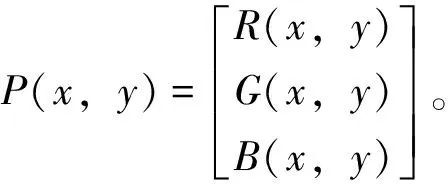
插值方法的价值在于，将有限的离散信息扩展为一个连续的信息系统，或者说，为离散信息补充了各种中间信息。不妨以红色分量来说明。

1)设Ri,j(1≤i≤m,1≤j≤n)是P(x,y)中第i行第j列像素的红色分量，它与像素平面上的二维点(i,j)相对应，构造一个二元函数Q(s,t)(0≤s≤m,0≤t≤n)， 使Q(i,j)=Ri,j， 并且Q(s,t)在任一点处达到连续。

2) 函数构造方法。

将矩阵R1={Ri,j;1≤i≤m,1≤j≤n)}扩充为R2={Ri,j;0≤i≤m+1,0≤j≤n+1}，即续上Ri,j(i=0,m+1或j=0,n+1)的值，这里采用外向插值法，取R0,j=2R1,j-R2,j(1≤j≤n)，Rm+1,j=2Rm,j-Rm-1,j(1≤j≤n)，Ri,0=2Ri,1-Ri,2(1≤i≤m)，Ri,n+1=2Ri,n-Ri,n-1(1≤i≤m)，R0,0=R0,1+R1,0-R1,1，R0,n+1=R0,n+R1,n+1-R1,n，Rm+1,0=Rm,0+Rm+1,1-Rm,1，Rm+1,n+1=Rm+1,n+Rm,n+1-Rm,n。然后将R2扩充为R3，其扩充方法与R2的方法相同。得到(m+4)×(n+4)的矩阵R′。由混合型多结点样条的曲面插值公式：

式中xi=1,2,…，m+4，yi=1,2,…,n+4，l1,l2为样点间距，这里设两个相邻像素点间距为1，即l1=l2=1。

曲面插值公式简化为

3)用同样的方法可以为P(x,y)的绿色分量G(x,y)和蓝色分量B(x,y)构造三次混合型多结点样条插值曲面。

Q(s,t)在整体上是连续的，因此，Q(s,t)是P(x,y)信息的一种连续表示，由于多结点样条的局部性，每段曲面只依赖于附近4×4个像素点的值，这就是下面加速方法的理论基础。另外一方面，插值曲面Q(s,t)具有一次严格性，当所有Ri,j共面时，Q(s,t)便是一个平面。如果P(x,y)表示一张色彩均匀变化的图像，任意放大，它仍然是均匀的。

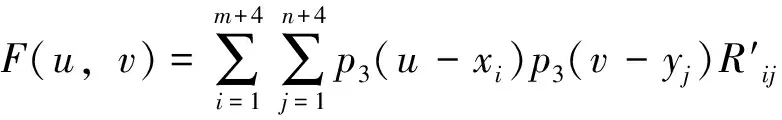
3 加速方法

由于多结点样条具有良好的局部性，像素点(i,j)的计算只依赖于其附近的4×4个像素点的值，即

F(u,v)=

图2 图像分块

试验表明，该方法可以提高计算速度，而且由系数矩阵近似所导致的误差较小，对图像质量的影响不大。

4 试验结果与分析

实验中从标准图像数据库里选取以下7副512×512测试图像(依次为Lena、House、Bird、Peppers、Avion、Butfish、Frog)来测试(见图3)。

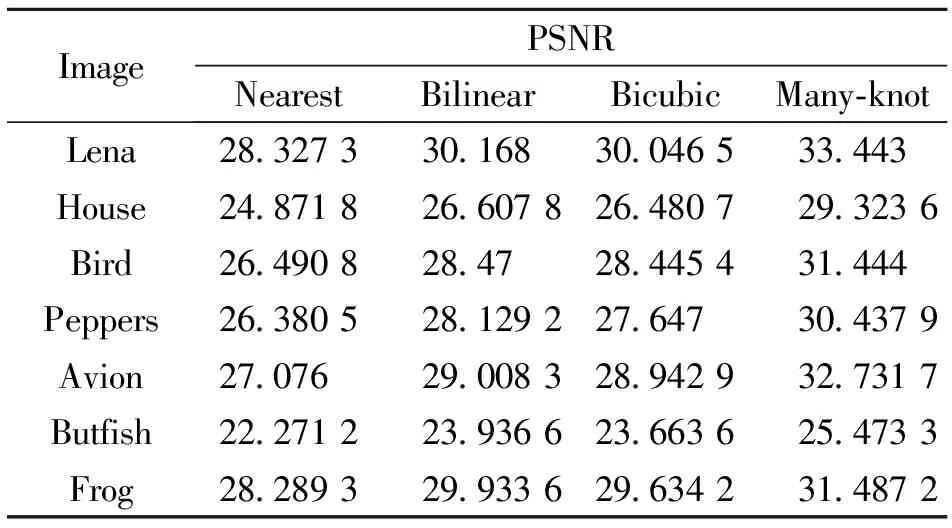
分别先将图像降采样为256×256大小的图像，采用不同的算法分别进行2倍系数的放大，生成512×512的结果图像。本文对四种算法进行了对照实验。第一种方法为邻近插值(Nearest)，第二种为双线性插值(Bilinear)，第三种为双三次插值(Bicubic)，第四种为混合型多结点样条插值(Many-knot)。采用信噪比(PSNR)、均值误差(ME)与梯度(Grads)来量化比较算法的优劣。从表1-3可以看出：除了在梯度方面，混合型多结点样条插值(Many-knot)略低于邻近插值(Nearest)外，混合型多结点样条插值(Many-knot)均优于其它三种算法。

图3 512×512测试图像

表1 各种算法PSNR的比较

Table 1 Comparing PSNR of each method

ImagePSNRNearestBilinearBicubicMany-knotLena28.327 330.16830.046 533.443House24.871 826.607 826.480 729.323 6Bird26.490 828.4728.445 431.444Peppers26.380 528.129 227.64730.437 9Avion27.07629.008 328.942 932.731 7Butfish22.271 223.936 623.663 625.473 3Frog28.289 329.933 629.634 231.487 2

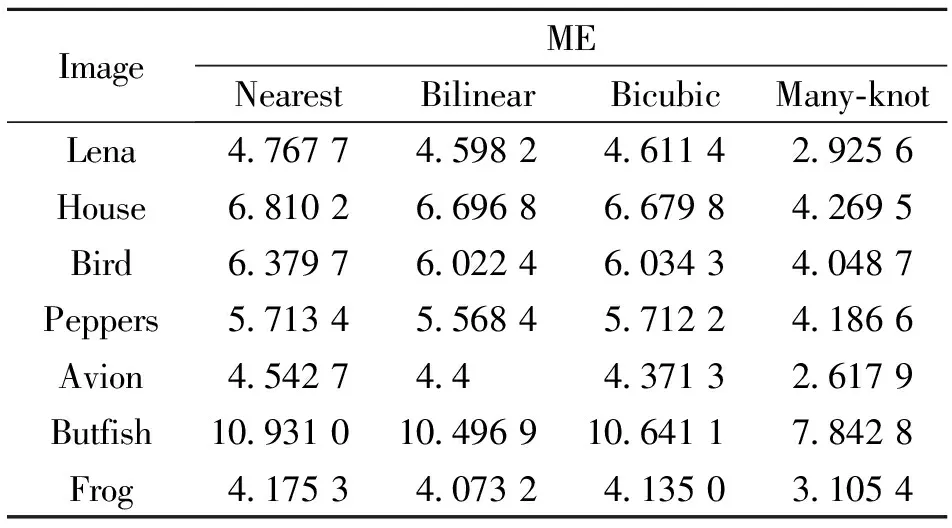
表2 各种算法ME的比较

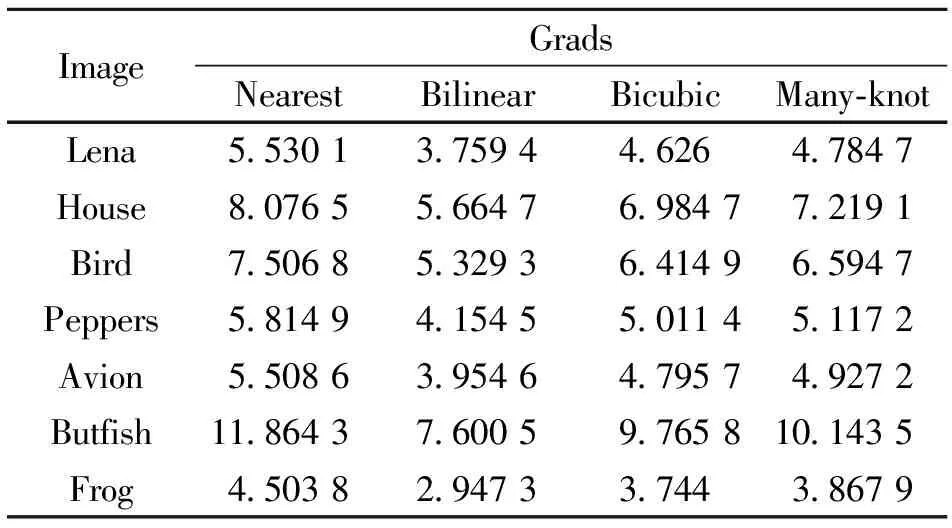
表3 各种算法Grads的比较

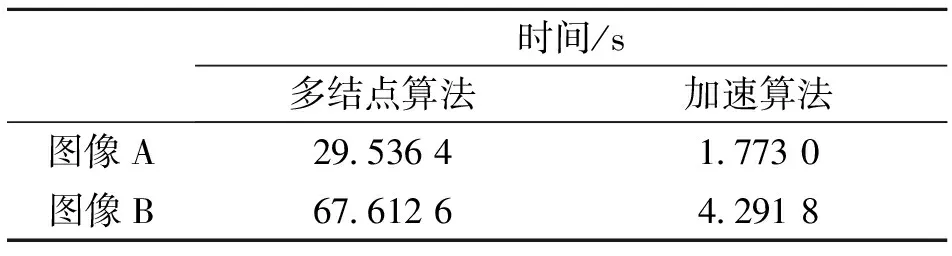
从以下两幅图像中分别取其一小块A，B。对小块图像A，B分别采用混合型多结点样条的加速方法与未加速方法将其放大4倍(见图4)。表4给出了多结点样条算法与加速算法时间上进行了对比，表明加速算法能提高10倍以上的速度。

图4 多结点样条算法与加速算法结果比较

表4 多结点样条算法与加速算法的时间对比

Table 4 Comparing consumed time of many-knot spline with its fast algorithm

时间/s多结点算法加速算法图像A29.536 41.773 0图像B67.612 64.291 8

5 结 论

本文引入多结点样条的混合型式，并将其应用于图像放大，该方法为数字图像的每一个色彩分量构造一个分块混合型多结点样条插值曲面。试验结果表明该方法对图像的放大质量较高。为了提高该方法的效率，提出一种加速算法。该加速算法在数字漫游系统与动画制作等方面可得到应用。今后，将多结点样条函数结合图像的梯度特征、各向异性及轮廓特征，开展进一步深入的研究。

参考文献：

[2]MEIJRING E，UNSER M. A note on cubic convolution interpolation [J]. IEEE Trans on Image Processing, 2003, 12(4):477-479.

[3]HWANG J W, LEE H S. Adaptive image interpolation based on local gradient features [J]. IEEE Signal Processing Letters, 2004, 11(3):359-362.

[4]ALY H A, DUBOIS E. Image up-sampling using total-variation regularization with a new observation model [J]. IEEE Trans on Image Processing, 2005, 14(10):1647-1659.

[5]PARK S C, PARK M K, KANG M G. Super-resolution image reconstruction: a technical review [J]. IEEE Signal Processing Magazine, 2003, 5:21-36.

[6]THEVNAZ P, BLUR T, UNSER M. Interpolation revisited [J]. IEEE Trans on Medical Imaging, 2000, 19(7):739-758.

[7]孙庆杰,张晓鹏,吴恩华.一种基于Bézier插值曲面的图像放大方法 [J].软件学报,1999,10(6):570-574.

[8]齐东旭. 关于多结点基数型δ-spline插值(Ⅰ)，(Ⅱ)，(Ⅲ)[J].吉林大学学报:自然科学版，1975(2):70-81；1976(2):36-44；1979(3):1-8.

[9]LI H S, DING W, QI D X. Many-knot spline interpolation and any-scale refinement algorithm [J]. Journal of Image and Graphics, 1997, 2(10):701-706.

[10]QI D X, LI H S. Many-knot spline technique for approximation of data [J]. Science in China (Series E), 1999, 29(4):334-387.

[11]齐东旭，田自贤，张玉心，等. 样条函数在飞机理论外形设计中的应用 [J]. 飞机设计，1982, 4:45-51.

[12]北方工业大学CAD研究中心与北京电视台.计算机卡通片《咪咪钓鱼》[CP ]. 北京：北京电视台，1991.

[13]北方工业大学CAD研究中心与北京科学教育电影制片厂.计算机电影片《相似》[CP].北京： 广播电影电视部电影发行局，1992.