我国居民家庭教育支出的影响因素分析

李亚伟，刘晓瑞

（浙江工商大学统计与数学学院，杭州310018）

0 引言

20世纪末，知识对经济与人的全面发展的重要性被提到了前所未有的高度。要获得知识，就必须依靠教育。舒尔茨(Theodore W.Schultz)指出：教育远不是一种消费活动。相反，政府和私人有意识地作投资，为的是获得一种具有生产能力的潜力，它蕴藏在人体内，会在将来做出贡献。而教育的发展水平直接受到教育支出水平的影响。尽管我国一直坚持教育的公益性质，突出政府在教育发展中的责任，但教育的资金投入不可能全部由国家财政包办，尤其在上世纪90年代末期，我国实行以扩招和收费制为核心内容的高等教育改革，使家庭分担的教育成本逐步上升，家庭在这一领域发挥着越来越重要的作用。在此背景下，考察哪些因素会影响我国居民教育支出的差异，具有一定的现实意义。本文在已有影响因素的基础上，结合社区因素，利用2006年中国健康和营养调查数据（CHNS），尝试使用分层线性模型分析方法研究我国居民家庭教育支出的主要影响因素。

1 数据和变量说明

本文使用的数据来自于美国北卡罗来纳大学和中国预防医学会2006年进行的中国居民营养和健康调查（CHNS）。这次调查在黑龙江、辽宁、山东、河南、江苏、湖北、湖南、广西和贵州9个省份，这些省份涉及中国的东、中、西不同的地区,涵盖了中国地区不同的经济发展水平,具有一定的代表性。该数据库采用多阶段随机抽样的方法，调查数据包含社区、家庭和个人层次资料，其中包含了教育和收入等方面的信息，符合本文研究的需要。本文选取的样本为有家庭教育支出并且有子女上学的家庭，同时考虑到样本信息的完全性，最终，本文的有效家庭样本总量为623个，有效社区样本总量为188个。

本文的研究对象为家庭教育支出。表1为各主要变量的说明及描述性统计。从表1中我们看到社区之间家庭的收入水平存在的较大的差异，从最小值的1937.75到最大值的67776.2。此外，在家庭内部，家庭收入水平、户主的受教育年限、子女所处的教育阶段等方面也存在着较大的差别。

2 模型和方法

对家庭教育支出的分析，不可避免地要涉及社会环境因素对家庭教育支出的影响，即家庭教育支出并非完全由家庭因素所决定，而是往往可能与社区居民的收入水平、教育的发展程度等相关，这些因素会导致同一社区不同家庭的教育支出存在相关性，从而违背了样本之间必须独立的统计原则。传统分析方法，如普通最小二乘和方差分析，都假设观察相互独立性，因而不适合分层数据的分析。1972年，Lindley和Simth提出了分层模型。分层模型解决了传统统计方法在分析分层结构数据时所遇到的问题。它不需要假设数据中的观察的独立性，在估计方法上,一般采用收缩估计和广义最小二乘法估计模型的系数,用受限的最大似然法或最大似然法估计方差成分和协方差成分,因而可以修正因观察数据的非独立性引起的参数标准误偏差。

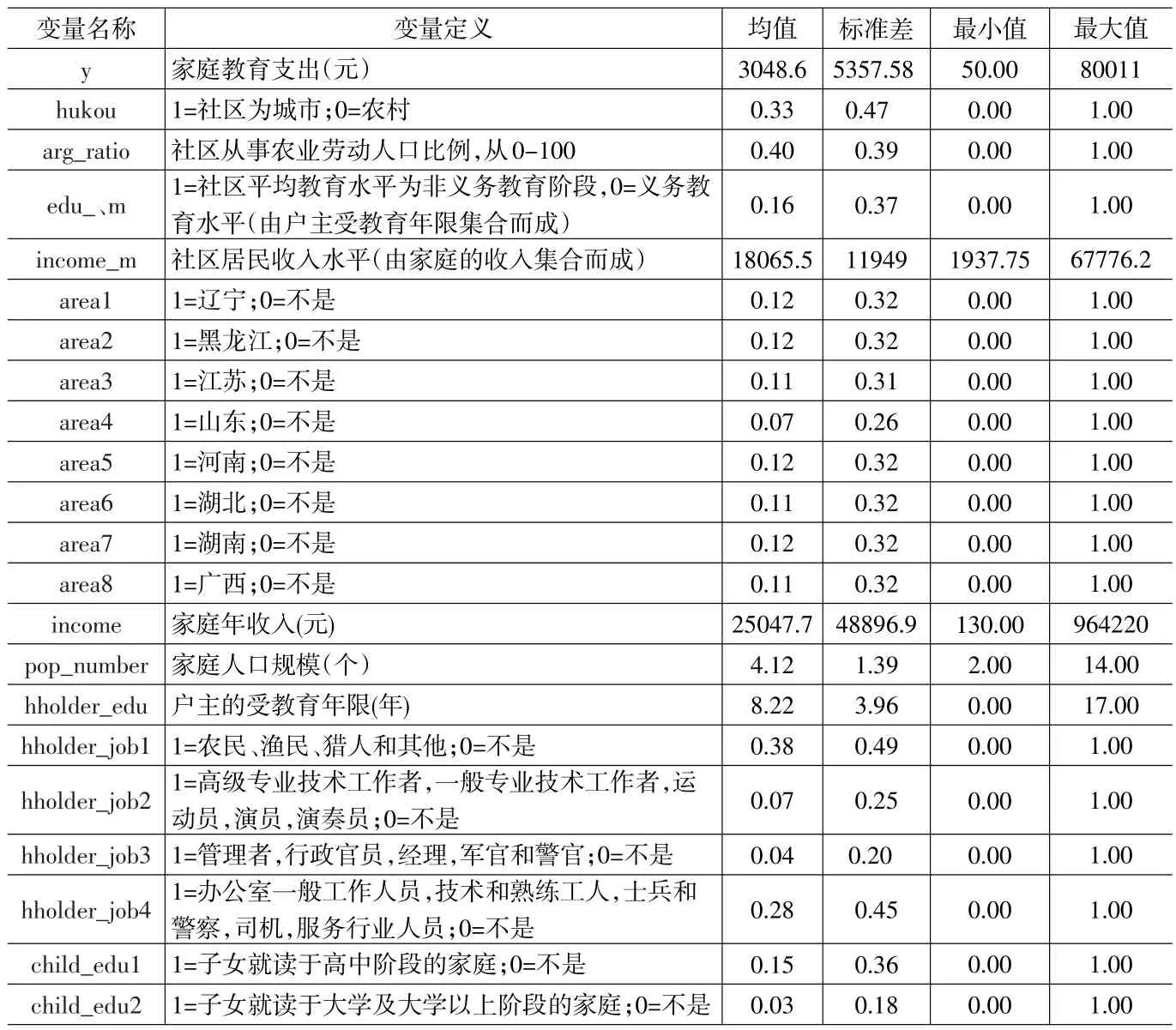
表1 变量的说明及描述性统计

结合本文变量和数据的特点，我们将采用二层线性模型对我国居民家庭教育支出的影响因素进行分析。具体而言，层一反映家庭特征，层二反映社区特征。本文所关心的是家庭因素和社区因素对家庭教育支出的影响，我们结合Hox(1994)和Singer(1998)所推荐的方法，在下面分层模型的建模过程中，我们以空模型来分析家庭教育支出的变异开始，然后依次建立随机截距模型、随机截距和随机斜率模型，来考察可能影响家庭教育支出的家庭和社区因素及其跨层交互作用。

首先，我们建立家庭层和社区层均没有解释变量的空模型。空模型是分层模型建模的基础，如式（1）。

其中，i代表家庭，j代表社区，yij表示第j社区中第i个家庭的教育支出；β0j表示第j个社区家庭的平均教育支出；γ00表示全部家庭平均教育支出；eij和μ0j分别为家庭层和社区层的随机误差项，并且满足

当空模型显示μ0j的方差统计显著时，我们应考虑对家庭教育支出进行分层模型分析，否则，用常规多元回归分析该数据便可。另外，空模型提供了社区特征对家庭教育支出影响的大小。根据经典定义,组内相关系数被定义为组间方差与总方差之比，即通过该系数，可以衡量社区之间教育支出的变异占家庭教育支出总变异的比例。ρ的值在0到1之间，ρ越大，则说明社区因素对家庭教育支出的作用越大。

如果式（1）显示社区之间教育支出存在显著差异，则我们将家庭变量和社区变量纳入空模型，探讨家庭和社区因素对教育支出的作用。假定社区之间平均教育支出存在显著差异，家庭层的斜率是固定斜率时，此时，称之为随机截距模型。如式（2）。

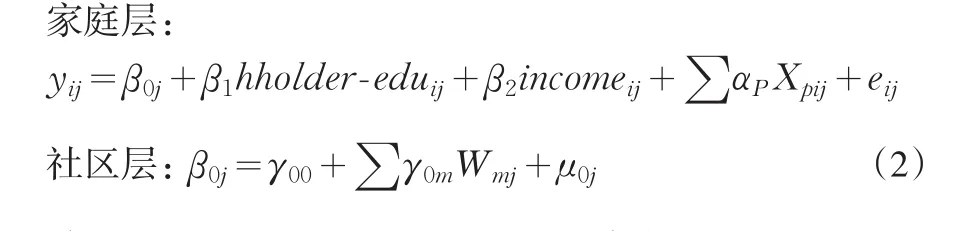
其中，hholder_edu为户主的受教育年限；income表示家庭收入；X为其他反映家庭特征的变量，包括户主的职业、子女所受的教育阶段、家庭人口规模。W表示社区层的因素，包括城乡变量、社区居民收入水平、社区平均受教育水平、农业劳动人口比例、地区虚拟变量等因素。

为了考察户主受教育年限与hukou变量是否存在不同层级的交互作用，我们对式（2）中户主受教育年限的斜率设为随机斜率，并加入hukou变量进行解释，此时，该模型为随机截距和随机斜率模型。如式（3）。

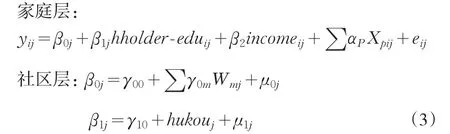
其中，hukou表示城市与农村的虚拟变量，μ1j为随机误差项

3 实证分析结果

3.1 空模型

本文使用HLM6软件演示分层模型，根据上文，我们首先对家庭教育支出进行空模型分析。

从表2的结果可以看出，组内相关系数（ρ）为0.14。该数值说明了家庭教育支出14%的可变性来自社区，86%的变异来自家庭，家庭教育支出的变异是由家庭和社区因素共同导致的结果。另外，我们看到，家庭教育支出在社区的变异十分显著。μ0j的p值为0.000，拒绝了各社区家庭教育支出无差别的原假设。因此，我们需采用分层模型技术，从而有效地分析各因素对家庭教育支出的具体影响。

3.2 随机截距模型

表2 模型1（空模型）分析结果

通过上述分析结果，我们知道家庭和社区特征会影响到家庭教育支出，但是具体有哪些因素影响，影响力如何并不知晓。下面我们在模型1中纳入家庭和社区变量，探讨它们对家庭教育支出的影响（见表3模型2）。与表2的分析结果相比较，就方差成分而言，社区层的变异值（）大大减少，从空模型（表2的模型1）中的3990013.13到随机截距模型（表3的模型2）的1000387.85，而家庭层次的变异值（σ2）仅从原来的24461871.38下降为22552324.57。根据公式我们算出社区和家庭因素对家庭教育支出变异的解释能力：模型2中社区变量大约解释教育支出在社区层次变异为75%。相反，家庭变量大约仅能解释教育支出的在家庭层次变异的7.8%。由此，这意味着社区因素对家庭教育支出的差异有比较强的解释能力。

从表3模型2的结果可以看出，家庭年收入对教育支出有显著的积极影响，这与其他研究相符。户主的受教育年限对家庭教育支出有显著的正影响。由于户主通常指的是父母，结果表明父母的文化程度每提高一年，其子女的平均教育支出会增加114.75元。我们认为这种正向关系归因于两方面的影响。一方面，父母受教育程度越高，根据人力资本理论，往往家庭收入水平就越高，也越有能力用于子女的受教育消费支出；另一方面，受教育程度越高的父母越希望子女的受教育程度超过自己，因而用于子女教育消费方面的支出就越多。从子女特征因素来看，子女所处的教育阶段对家庭教育支出有显著的影响（p＜0.001）。与子女就读初等教育阶段的家庭相比，有子女就读于中等阶段和高等阶段的家庭，其教育支出分别增加3119.50和6871.20。家庭人口规模对家庭教育支出有显著的正影响。户主职业对教育支出的影响不具有统计显著性。

表3模型2还显示了尽管城乡因素作用方向与预期相同，即城市家庭的教育支出高于农村家庭，但城乡因素对教育支出并不产生显著影响。这可能与目前社会对高学历人才的大量需求以及所带来的社会就业结构的变化有关,每个家庭都迫切希望子女能有上大学的机会，城乡居民不惜代价给孩子创造好的教育条件。社区居民的收入水平对家庭教育支出有积极的影响，这种影响具有统计上的显著性。这个结果证明了我们的观点，即社区居民的收入水平是影响我国居民家庭教育支出的重要解释变量。我们认为教育消费作为消费的一种类型，也具有消费的一般特征，即J.Duscnberry（1949）提出的消费行为的“示范效应”。这就表明家庭教育支出是非独立的，家庭教育消费行为不仅受自身收入的影响，也受周围家庭教育消费水平的影响。社区居民的收入越高，则往往周围家庭的文化消费气氛较浓，即使某个家庭的收入水平较低，也企图接近周围家庭的教育消费水平，于是教育消费就会越高。家庭教育支出的省际差异也十分明显，与贵州省相比，黑龙江、江苏、湖北和湖南省份的家庭教育支出都显著偏高。

3.3 随机截距和随即斜率模型

模型2分析了社区变异和家庭变异，并假定家庭因素对教育支出的影响在社区之间是恒定，但我们不能忽视家庭因素和社区因素因素互动的可能性。模型3在模型2的基础上，设户主受教育年限斜率为随机，并加入城乡变量进行解释，引入交叉项。因而我们可以检验户主受教育年限的斜率是否因城乡而异。

从表3模型3的结果来看，与模型2相比，模型的拟合改善了。当二个模型嵌套时，偏差度差异可以用来评估模型拟合度的改善，一个经验法则是两个模型的偏差度的差值必须是两个模型估计参数数目差异的两倍以上。模型3比模型2偏差度减少了14.5，而模型估计的参数只多了一个，从而显示模型3拟合的改善具有统计显著性。总体而言，模型3和模型2显示的数值，无论是系数还是标准误，二者相差不大。户主受教育年限纳入随机斜率对家庭层次变量的系数几乎毫无影响。然而，模型3改变了部分社区因素对家庭教育支出的作用。社区居民收入和湖北地区的虚拟变量仅在随机截距模型中对教育支出产生显著影响。这表明，当模型允许低层因素对高层因素互动时，高层因素的作用受到削弱——部分高层因素对因变量的影响实际上是通过低层因素实现的。

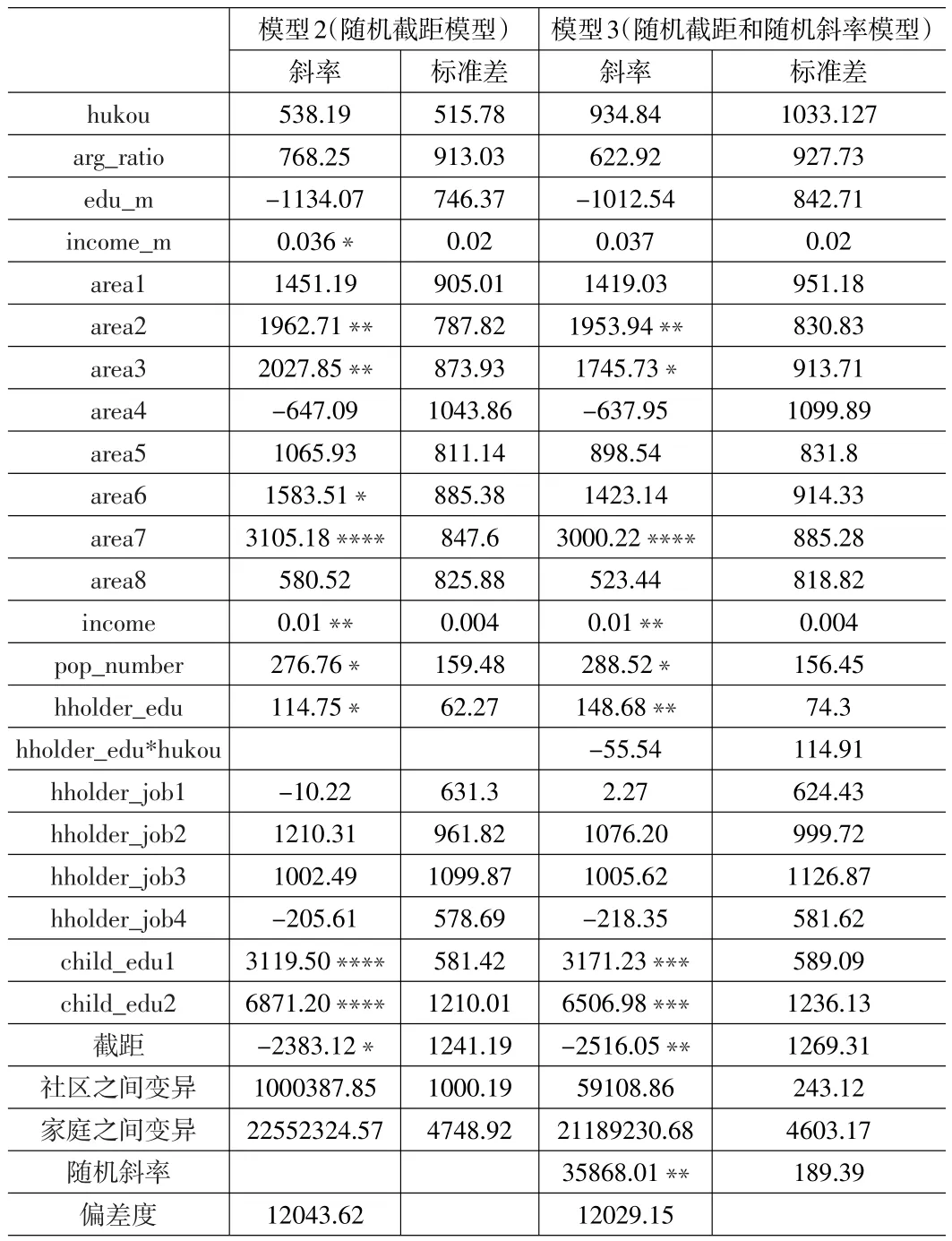
表3 模型2和模型3的分析结果

此外，我们发现，模型3中户主受教育年限与城乡变量的交互项并不显著，也就是说，户主受教育年限对家庭教育支出的影响在城乡之间并不存在显著的差异。我们认为，无论在城市或农村，受过良好教育的父母，本身就是教育的受益者，他们倾向于认为投资子女的教育将获得极大的未来收益，因而都会增加对子女的人力资本投资。我们还可以发现户主受教育年限斜率随机变量的变异依然显著，这意味着，一方面，社区之间的差异的确影响户主受教育年限对家庭教育支出的影响；另一方面，由于数据的局限，模型3遗漏了其他影响户主受教育年限的重要因素。

4 结论和启示

本文利用2006年CHNS数据并采用二层线性模型，对我国居民家庭教育支出的影响因素进行分析，重点考察了社区因素对家庭教育支出的影响。研究结果表明，社区间家庭的教育支出存在着显著的差异；社区居民收入水平对家庭教育支出的影响是不可忽视的，社区居民收入水平是影响家庭教育支出的重要因素之一；户主的教育水平的提高有利于增加对子女教育的支出，并且城乡户主的教育水平对家庭教育支出的影响没有显著差异；最后，家庭收入水平、家庭人口规模和子女受教育阶段变量对家庭教育支出有显著的正影响。

从上述实证分析的结果中我们可以得到两点启示：（1）发展经济发展落后社区的经济，从而缩短由于社区收入水平造成的家庭教育支出差距。（2）努力改善家长的教育素质，进一步增强他们对子女教育质量的偏好，从而增加家庭对子女教育的投入。

[1]李红伟.中国城镇居民家庭教育消费实证研究[J].教育与经济，2000，（4）.

[2]孙彩红.重庆市中小学生教育支出差异性分析[J].重庆工商大学学报，2003，（2）.

[3]雷万鹏等.中国农村家庭教育支出的实证研究：1985～1999[J].教育理论与实践.2003，（7）.

[4]雷万鹏.高中生教育补习支出：影响因素及政策启示[J].教育与经济，2005，（1）.

[5]丁小浩，薛海平.我国城镇居民家庭义务教育支出差异性研究[J].教育与经济，2005，（4）.

[6]杨菊华.多层模型在社会科学领域的应用[J].中国人口科学，2006，（3）.

[7]陈俊华等.从分层模型视角看出生人口质量的影响因素——以江苏省无锡市为例[J].中国人口科学，2006，（3）.

[8]楚红丽.基础教育阶段家庭教育支出影响因素的研究述评[J].教育学报，2006，（12）.

[9]王海港等.城镇居民教育收益率的地区差异及其解释[J].经济研究，2007，（8）.

[10]王济川.多层统计分析模型—方法与应用[M].北京：高等教育出版社，2008.

[11]许玲丽等.成人高等教育的工资效应[J].经济研究，2008，（12）.

[12]薛海平、丁小浩.中国城镇学生教育补习研究[J].教育研究，2009，（1）.

[13]宁光杰.教育扩张能改变收入分配差距吗?[J].世界经济文汇，2009，（1）.

[14]杨汝岱.高等教育改革、预防性储蓄与居民消费行为[J].经济研究，2009，（8）.

[15]楚红丽.我国中小学课外补习家庭之背景特征及个人因素[J].教育学术月刊，2009，（12）.

[16]Filippa Bono.Regional Inequalities in Consumption Patterns:A Multilevel Approach to the Case of Italy[J].International Statistical Review,2007，(75).

[17]Maria M.Ciarleglio.Hierarch Linear Modeling:An Overview[J].Child Abuse Neglect,2007，(31).