基于DSP+FPGA的交流伺服驱动器设计

刘日宝，王爱祥

(南京电子技术研究所，江苏南京210013)

0 引 言

随着电力电子技术和现代控制理论的发展，以永磁同步电动机为执行元件的全数字交流伺服驱动系统，其性能已和直流伺服系统相当，而交流电机的环境适应能力和低维护成本则成为取代直流伺服的最大优势。本文研究目的就是为现代雷达装备提供一种高可靠性的交流伺服驱动装置，取代传统的直流伺服驱动系统，在满足雷达对恶劣的环境适应性要求的同时，降低系统的维护成本。

1 交流伺服驱动器的控制策略分析

1.1 电流控制器设计

1.1.1 矢量控制

矢量控制是19世纪70年代前西德Blaschke等人提出来的［1］。采用固定于永磁同步电动机转子的dq旋转坐标系，如图1所示。图中αs为定子A相轴线，β为定子电流矢量is的空间相角，id和iq就是is在旋转坐标系dq轴上的两个分量，如果得到了id和iq，也就确定了定子电流矢量的相角和幅值，矢量控制就是通过对这两个电流分量id和iq的控制来实现的。

图1 永磁同步电动机空间矢量图

1.1.2力矩电流比最大控制

基于矢量控制的永磁同步电动机电流控制方法主要有:(1)id=0控制;(2)力矩电流比最大控制;3)功率因数等于 1 的控制;(4)恒磁链控制［2－3］。功率因数等于1和恒磁链的电流控制方法［4］，其电动机输出力矩都受到了限制，一般不考虑采用。

1.1.3 仿真计算

采用如图1所示的dq旋转坐标系，电机的转矩公式可以表示［1］:

由上式可以看出，电机的输出转矩是定子电流is和定子电流空间相角β的双元函数。

设电机永磁体磁链ψf=0.24 Wb，Ld=8 mH，Lq=9 mH，应用Matlab对转矩进行计算仿真，得到如图2所示的电机转矩输出图。

由于电机的定子电流不能无限制增大，考虑电机本身的过载能力，一般不能超过额定电流的2～3倍，同时电流输出还受逆变器容量和直轴去磁电流的限制。假设定子电流从25%额定值变化到200%，则永磁同步电动机的转矩输出如图3所示。

图2 永磁同步电动机的转矩输出图

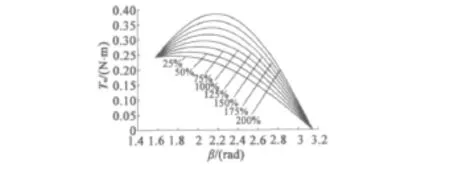
图3 不同的定子电流时永磁同步电动机的输出转矩和转矩角β的关系

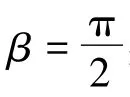
1.1.4 电流控制器结构

为了实现转矩的快速稳定地响应与发挥电机的最大输出能力，本系统的电流环节最终采用PI调节结合力矩电流比最大控制方法。该电流控制器结构如图4所示。

1.2 速度控制器设计

速度控制器的设计采用了Bang－Bang控制的PI调节器，控制器结构如图5所示。该速度控制器一方面极大地改善了系统速度环节的动态性能，另一方面由于引入了转速微分负反馈［3］，使得超调明显地减小甚至消除了。

图4 交流伺服系统的电流控制器

图5 交流伺服系统的速度控制器

1.3 位置控制器设计

伺服系统的位置控制，追求的是快速性、准确性和无超调。一般我们将位置伺服系统定位过程划分为加速、恒速、减速和低速趋近定位点四个阶段。在加速、恒速和减速阶段，位置控制器采用常系数比例调节器，最大限度地提升系统的快速性能。而最重要的是低速趋近定位点阶段，由于该阶段电机速度很低，无论对系统的定位时间，还是对系统的最终定位精度都有着重要的影响，此时若采用纯比例调节器，显然不能快速而无超调的定位，因此本文采用如图6所示的变结构加速度控制器 VSAC［5－6］。即:

图6 变结构加速度控制器

于是误差的状态方程:

取切换线:

2 交流伺服驱动器硬件设计

交流伺服驱动器的硬件主要由主控板和功放板组成，其硬件组成如图7所示。

图7 系统硬件框图

2.1 主控板

主控板的核心为DSP、FPGA与RDC转换电路。DSP采用的是TMS320LF2407A，该芯片是TI公司专门为电机控制设计的，它有着丰富的外设资源，指令周期最低可至25 ns，完全能够满足伺服控制的实时性要求。FPGA是Altera公司的EP1K50QI208－2，如图7所示，它实现了RDC的解算与控制，并且采用并行数据总线，实时地将位置数据传送给DSP，此外，ADC数据采集与处理、故障综合与保护也由FPGA来实现。

2.2 功放板

功放板的核心为IPM和EPLD。IPM是三菱公司的第五代智能功率模块PM75RLA060，该模块集成度高，保护功能完善，采用该模块能够极大地提高驱动器的可靠性与维修性。EPLD采用的是Altera公司的EPM7064STI44－7，主要实现了驱动器的过热、过流、过载等保护功能。

3 实验结果

交流伺服系统的实验平台主要由电源、伺服驱动器、永磁同步电动机、减速机、转矩测量仪、磁粉制动器和电流控制器组成，其结构如图8所示。电机为一台2.2 kW永磁同步电动机，主要参数:额定转矩7 N·m，额定电流8 A，额定转速3 000 r/min，额定电压220 V，允许两倍过载，减速箱变比为1∶2。应用此实验平台，进行了伺服驱动器的一系列实验。

图8 交流伺服系统实验平台

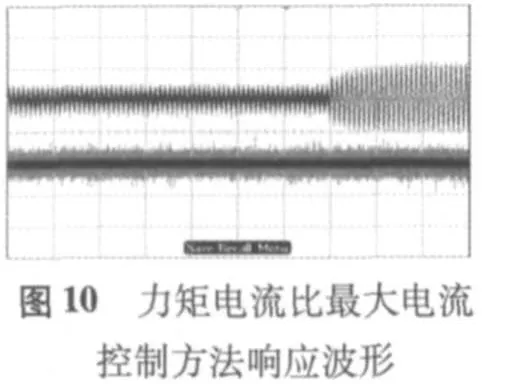
电流控制器的性能直接决定驱动器的力矩输出能力，如图8所示，当驱动器给定转速等于600 r/min时，分别采用id=0和力矩电流比最大控制方法，得到波形图如图9和图10所示。图中上面的曲线为电机实际相电流，下面的曲线为速度。在电机的速度不下降的情况下，电机负载端通过磁粉制动器突然施加最大阻力，图10采用力矩电流比最大控制方法，相比图9采用id=0的电流控制方法，电机的实际电流要大，电机输出的转矩提升了将近7%。

在电机电流一定，并且限制在两倍的额定值之内时，得到实际的电机空载电流和电机输出力矩与转矩角的数据，画成曲线如图11所示。由图可以看出，电机输出转矩与转矩角关系曲线与图3的计算仿真曲线类似，同时电机的空载电流也随着转矩角的偏移，在力矩输出最大点达到最小。

图11 两倍额定电流时转矩输出与转矩角关系曲线

图12和图13分别是位置控制环节采用纯P校正和变结构P校正的系统位置阶跃响应波形，上面的曲线是速度，下面的曲线是位置。系统的速度环节采用了微分负反馈PI校正结合Bang－Bang控制，由图可以看出，系统速度上升曲线平滑快速，基本无超调，无振荡。图13相比图12的位置响应快速，而且无超调，无振荡，证明该位置控制器有着良好的性能。

4 结 语

综上所述，本文研制的基于DSP+FPGA的交流伺服驱动器，具有硬件结构紧凑、可靠性高的特点，而采用现代控制理论结合经典控制方法，充分发挥了灵活的软件伺服能力，获得了良好的驱动性能，能够满足雷达对伺服系统的一般要求，该驱动器目前已经实现了工程应用。

［1］ 王成元.矢量控制交流伺服驱动电动机［M］.北京:机械工业出版社，1995.

［2］ 李志民，张遇杰.同步电动机调速系统［M］.北京:机械工业出版社，1996.

［3］ 陈伯时.电力拖动自动控制系统［M］.北京:机械工业出版社，1991.

［4］ Morimoto S，Takeda Y，Hirasa T.Current phase control methods for permanent magnet synchronous motors［J］.IEEE Trans.on PE.1990，5(2):133 －139..

［5］ 姚琼荟，黄继起，吴汉松.变结构控制系统［M］.重庆:重庆大学出版社，1997.

［6］ Lai C，Shyu K.A novel motor drive design for incremental motion system via sliding － model control method［J］.IEEE Trans.on Industrial Electronics，2005，52(2):499－507.