考虑统计不确定性的结构可靠度分析方法

吕大刚，宋鹏彦，王光远

(哈尔滨工业大学 土木工程学院，150090哈尔滨，ludagang@hit.edu.cn)

考虑统计不确定性的结构可靠度分析方法

吕大刚，宋鹏彦，王光远

(哈尔滨工业大学 土木工程学院，150090哈尔滨，ludagang@hit.edu.cn)

为了充分研究统计不确定性对结构可靠度的影响，本文将综合考虑物理不确定性和统计不确定性，以Bayes理论为数学工具，对结构的统计可靠度问题进行研究.首先对Bayes理论进行概括和总结，采用该理论对结构工程中的统计不确定性进行建模和分析.然后研究考虑统计不确定性的结构可靠度分析方法，给出考虑统计不确定性的各种结构可靠性测度，并研究综合考虑主观不确定性与客观不确定性的整体式与分离式可靠度计算方法.最后通过2个算例，分析了统计不确定性对结构可靠度的影响.

随机可靠度;统计可靠度;物理不确定性;统计不确定性;Bayes统计学

结构工程中的随机性包括物理不确定性、统计不确定性和模型不确定性，物理不确定性是指各种物理量(如荷载、材料强度、结构尺寸等)的客观变异性;统计不确定性是由于对物理量进行统计分析时缺乏足够的样本信息而产成的;模型不确定性则源于对复杂物理现象进行数学建模时的理想化假设.传统的结构可靠度理论属于随机可靠度理论，因为它处理的主要是物理不确定性问题;而经典可靠度理论则更多地考虑统计和模型不确定性问题［1］.目前，在结构可靠度理论的研究领域，对于考虑统计不确定性和模型不确定性的结构统计可靠度问题，研究得还不充分，有必要将上述2个领域的可靠度问题和方法进行融合.

Egeland［1］较早注意到了结构随机可靠度与经典统计可靠度2个学科之间的分野，并提出了将这2种理论进行融合的建议.对于模型不确定性对结构可靠度的影响问题，国内外结构设计规范当前的统一处理方法是在考虑材料性能和几何参数随机性的抗力模型基础上，引入一个考虑计算模式随机性的随机变量，以考虑模型不确定性的影响.对于考虑统计不确定性的结构可靠度问题，目前国内外研究较少.Greimann等［2］采用经典统计学中的区间估计方法对统计不确定性进行定量化，提出带有一定置信度的可靠度计算方法，并对某一桁架结构进行了概率可靠性分析.Lemaire等［3］对统计数据不确定性对结构可靠度的影响进行了初步研究.Igusa等［4］采用Bayes分析技术较系统地研究了结构工程中的不确定性.Der Kiureghian 等［5－7］深入研究了在不完全知识状态下结构安全性的各种测度，研究了基于主观认识上的统计不确定性对系统可靠度和时变可靠度的影响.Faber等［8－10］在工程概率决策分析中考虑了统计不确定性的影响，并采用Bayes技术对统计数据进行更新.从目前发展趋势看，对于统计可靠度问题，Bayes统计学大有代替经典统计学的趋势，特别是随着马尔可夫链蒙特卡洛(Markov Chain Monte Carlo，MCMC)模拟法的快速发展，后验统计量和预测分布的计算已不存在困难.

本文将综合考虑物理不确定性和统计不确定性，以Bayes统计学为数学工具，对结构的统计可靠度分析方法进行深入细致的研究.

1 统计不确定性的Bayes建模与修正

1.1 Bayes修正公式

在Bayes统计学中，Bayes公式通过来源于观测数据的似然函数修正先验概率分布，从而将主观信息与客观信息进行有机集成

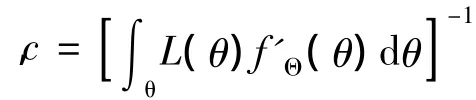
确定先验分布的方法主要有主观先验分布、扩散先验分布、无信息先验分布、共轭先验分布等方法;似然函数是根据客观信息通过似然原理确定的;后验分布实际上是给定样本观测值x后θ的条件分布:f″Θ(θ|x)∝L(θ|x)f'Θ(θ)，后验分布一旦得到，即可得到Θ的平均值和标准差等后验统计信息.

1.2 统计不确定性的建模与分析

利用Bayes修正公式(1)可以对统计不确定性进行建模与分析.

设f(x，θf)为随机向量X的联合概率密度函数，θf为考虑统计不确定性的分布参数.当随机试验的观测值表现为等式观测(例如混凝土强度的统计分析)时，似然函数L(θf)可以取为

式中x1，x2，…，xn是X的随机抽样的一组观测数据.

如果抽样不是随机的，则必须使用样本值的联合分布建立似然函数，此时可以通过对于x的不等式观测(例如桥梁的荷载验证试验)来取代对于 x的直接观测.假设不等式观测事件为Ei={gi(xi)≤0}，i= 1，…，n，并假设 xi是统计独立的，则有

2 考虑统计不确定性的结构可靠性测度

将统计不确定性参数记为θf，则考虑统计不确定性的结构失效概率为

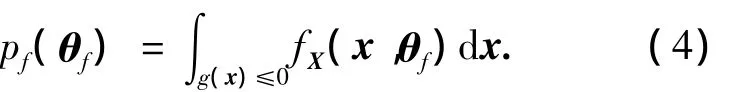
对于统计参数θf，通常有3种数学处理方法:点估计、区间估计和预测估计，相应地也有3种结构可靠性的测度.

2.1 统计可靠度的点估计

式中Φ－1(·)为标准正态累积分布函数(CDF)的反函数.

2.2 统计可靠度的区间估计

考虑某个统计参数θ∈θf，根据给定的置信水平α，寻求满足式(6)的θ'和θ″，称为θ的区间估计问题.

β的平均值和方差可按下式计算

式中 ▽θfβ(μθf)表示可靠指标 β 对向量 θf的梯度在μθf处取值.根据式(6)和式(7)即可得到可靠指标的区间估计为μβ±σβ.

2.3 统计可靠度的预测估计

根据Bayes统计学的基本原理，pf(θf)的Bayes估计为其后验均值，即

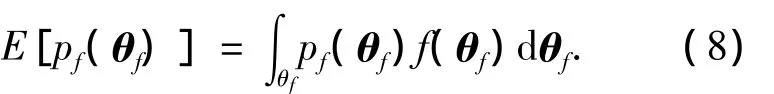
式中f(θf)为θf的后验PDF.

根据Fubini定理，有

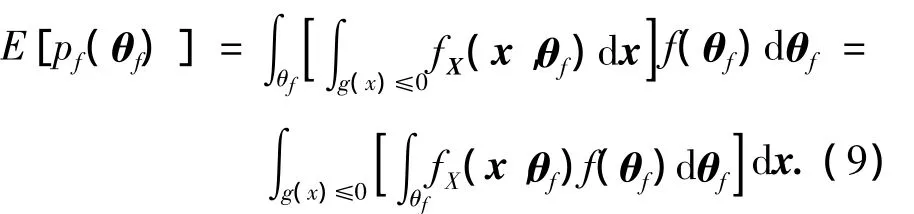
3 考虑统计不确定性的结构可靠度分析方法

物理不确定性属于客观不确定性，而统计不确定性则属于主观不确定性.根据对于主观和客观不确定性数学处理方法的不同，结构的统计可靠度分析有以下2种分析方法.

3.1 主观与客观不确定性的整体式分析方法

3.1.1 联合分析(整体式分析方法1)

将θf与x同等对待，亦即将θf也视为随机变量，将其与x连同一起组成扩展的随机向量，然后采用经典的随机可靠度理论进行分析，失效概率为

通常情况下，可以假设随机向量x，θf相互独立，于是可以采用经典的FORM、SORM或重要抽样(Importance Sampling，IS)等方法对式(11)进行一次随机可靠度分析即可得到可靠指标和相应的失效概率.

3.1.2 预测分析(整体式分析方法2)利用x的预测分布来计算结构的失效概率

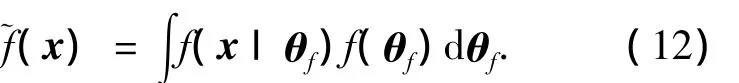
将式(12)代入到式(11)中，可得到预测失效概率为

式(13)为给定当前样本时，未来观测值的预测失效概率.

3.1.3 嵌套分析(整体式分析方法3)

引入一个新的极限状态函数

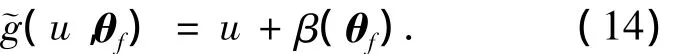
式中:u为标准正态随机变量，并与 θf独立;β(θf)为统计不确定性参数 θf的条件可靠度指标.

相应于式(14)的失效概率为

由于u为标准正态随机变量，因此上式中方括号内的积分为

将式(16)代入式(15)，可得

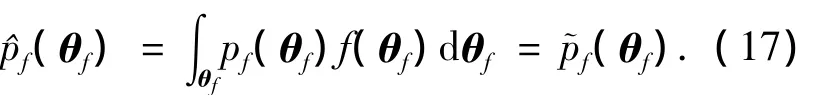
3.1.4 近似分析(整体式分析方法4)

因此，预测可靠指标可以近似为

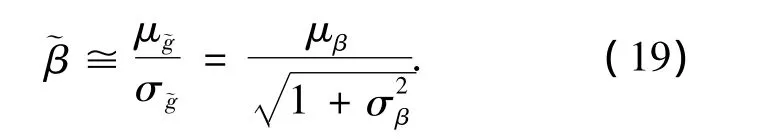
式中:μβ=E［β(θf)］，σβ为考虑主观不确定性的可靠指标标准差，由式(7)求得.

3.2 主观与客观不确定性的分离式分析方法

与整体式分析方法同时处理主观和客观不确定性不同，这种方法将β(θf)单独视为一个随机变量进行统计可靠性分析.

随机变量β(θf)的累积分布函数(CDF)为显然，这是一个嵌套可靠度分析问题，内层需要首先计算 β (θf)，外层再计算 Fβ(θf)(b).

β(θf)的概率分布函数(PDF)为

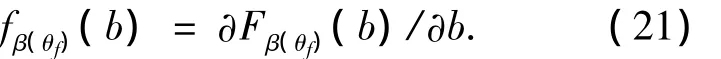
显然，这是结构可靠度理论中的灵敏度分析问题.

将 β(θf)在 M″θf处近似展开为一次 Taylor级数形式，可以得到β(θf)的一次近似为

式中:M″θf为 θf的后验平均值，Σ″θf为 θf的后验协方差矩阵.

4 算例分析

4.1 数值算例分析

考虑极限状态函数

式中:随机变量 X1和 X2服从正态分布，即X1～N(μ1，σ1=20)，X2～ N(μ2，σ2=15).参数向量为θf= ［μ1，μ2］T，并且对于X1有n1个样本，样本均值1=100;相应的X2有n2个样本，其均值为2=50.

这里假设均值μ1和μ2的先验分布为无信息先验分布，根据Bayes修正准则，可得后验分布为

下面进行可靠指标的估计，根据可靠指标的定义有

4.1.1 可靠指标的点估计

依据式(7)和(24)，利用后验均值可得可靠指标β的点估计值:

4.1.2 可靠指标的区间估计

根据分离式分析方法，利用μβ和σβ的一次近似，即由式(22)可得

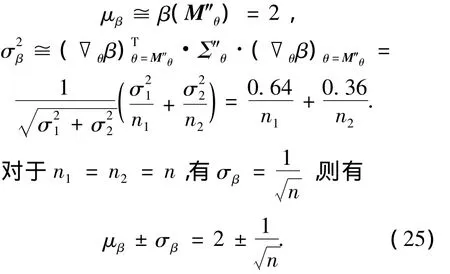
对n取不同值，由式(25)得可靠指标所在的区间，列入表1.

从表1可以看出，随着样本数的增加，由于统计不确定性所引起的可靠指标的变化范围逐渐缩小，并向β的均值靠近.这说明，样本数的增加使分布所含的统计不确定性减小，其可信程度提高，从而使β向真值靠近.

表1 可靠指标区间与样本数n的关系

4.1.3 可靠指标的预测估计

根据Bayes原理，可得X1和X2的预测分布为

此外，也可以采用整体分析方法中的近似分析，即由式(18)可得

此式与式(27)等同.

由此可知，可靠指标与样本的数量n1和n2有关，假设n1=n2=n，则式(27)可表示为

表2 预测可靠指标与样本数n的关系

表2 预测可靠指标与样本数n的关系

n 5 6 7 8 9 10∞1.826 1.852 1.871 1.886 1.897 1.907 2.000

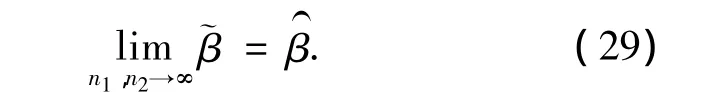
4.2 考虑统计不确定性的断裂可靠度分析

众所周知，焊接的裂缝尺寸是随机的.假设超过某一特定尺寸s0的概率密度函数

是关于参数θ的移位指数分布，希望在裂缝尺寸资料的基础上对θ进行估计.假设通过对某一段焊缝观测，参数θ的似然函数可表示为

当s0=0.1 cm，v=2 cm和k=11时，参数θ的后验均值=k/v=5.5 cm－1，则可得裂缝尺寸的概率密度函数，如图1所示.

由图1可知，考虑θ不确定性的预测分布显示极端裂缝尺寸的概率增大.

下面考虑压力管道焊接裂缝的问题:假设管道长l=1 000 m，且焊接处产生的裂缝是均值比为λ的随机泊松分布，希望确定焊接裂缝尺寸Smax的概率分布.一般从泊松分布中随机抽取的分布其分布类型不变，由此可得

图1 裂缝尺寸的概率密度函数

若已知Smax关于λ和θ的条件分布，则可得Smax的预测余累积分布函数(CCDF)，如图2所示.图中s0=0.1 cm，λ是服从参数k=10和v=120 cm的Gamma分布，θ也是服从参数k=11和v=2 cm的Gamma分布.由图可知:考虑统计不确定性的结果降低了裂缝尺寸的概率.

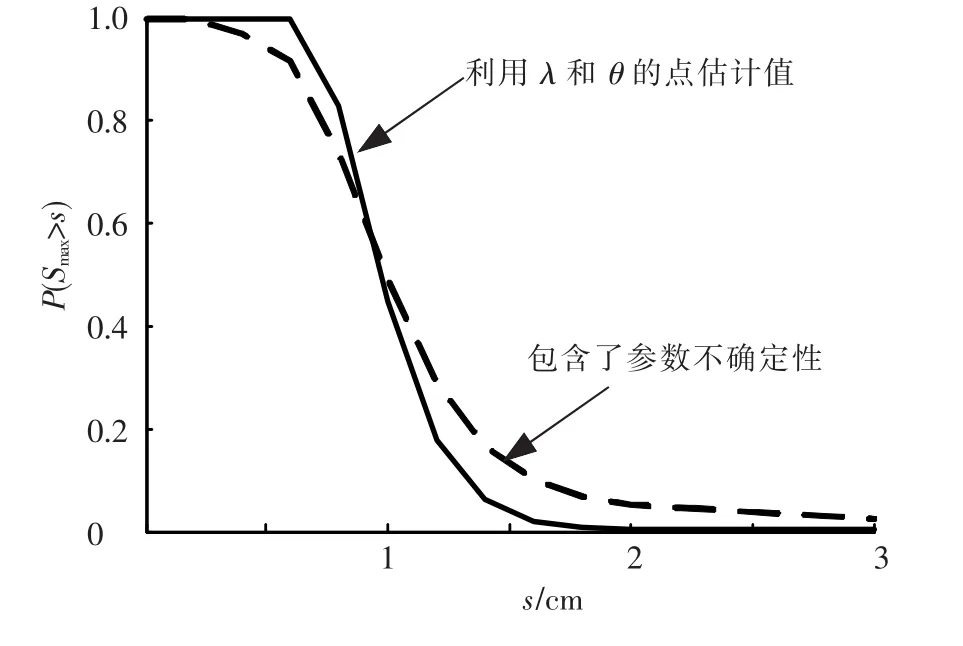
图2 最大裂缝尺寸的CCDF

5 结语

应用Bayes统计学，系统地研究了考虑统计不确定性的结构统计可靠度理论，给出了考虑统计不确定性的各种结构可靠性测度，并研究了综合考虑主观与客观不确定性的整体式与分离式可靠度计算方法.通过算例分析表明，统计不确定性对只考虑客观不确定性的随机可靠度有很大影响.预计统计可靠度理论将会被广泛应用于结构的安全评定、健康监测和寿命预测中.

［1］ EGELAND T.Two trends in reliability［J］.Structural Safety， 1991，9(4):261－268.

［2］ GREIMANN L F，KNAPP W J，YEUNG J Y．Propagation of certainty levels［J］．Journal of Structural Engineering， 1985，110(9):1935－1948．

［3］ LEMAIRE M，MOHAMED A，PENDOLA M，et al．Uncertainties in the treatment of statistical data and influences on the structural reliability assessment［C］//Proceedings of Lifetime Management of Structures．Paris:ESReDA，2003:98－108．

［4］ IGUSA T，BUONOPANE S G，ELLINGWOOD B R．Bayesian analysis of uncertainty for structural engineering applications［J］．Structural Safety， 2002，24(2/3/4):165－186．

［5］ DER KIUREGHIAN A．Measures of structural safety under imperfect states of knowledge［J］．Journal of Structural Engineering， 1989，115(5):1119－1140．

［6］ DER KIUREGHIAN A．Analysis of structural reliability under parameter uncertainties［J］．Probabilistic Engineering Mechanics， 2008，23(4):351 －358．

［7］ DER KIUREGHIAN A，DITLEVSEN O．Aleatory or epistemic?Does it matter?［J］．Structural Safety， 2009，31(2):105－112．

［8］ FABER M H，MAES M A．Epistemic uncertainties and system choice in decision making［C］//Proceedings of the 9th International Conference on Structural Safety and Reliability．Rome:ICOSSAR，2005:3519－3526．

［9］ FABER M H，MAES M A．Epistemic uncertainties in decision making［C］//Proceedings of the 24th International Conference on Offshore Mechanics and Arctic Engineering．Halkidiki:ASME，2005:1 －8．

［10］ FABER M H．On the treatment of uncertainties and probabilities in engineering decision analysis［J］．Journal of Offshore Mechanics and Arctic Engineering， 2005，127(3):243－248．

［11］ WEN Y K，CHEN H C．On fast integration for time variant structural reliability［J］．Probabilistic Engineering Mechanics， 1987，2(3):156－162．

Reliability analysis methods of structures considering statistical uncertainty

LÜ Da－gang，SONG Peng－yan，WANG Guang－yuan

(School of Civil Engineering，Harbin Institute of Technology，150090 Harbin，China，ludagang@hit.edu.cn)

In order to fully investigate the influence of statistical uncertainty on reliability of structures，in this paper，the statistical reliability theory of structures considering two kinds of uncertainties，i.e.，physical uncertainty and statistical uncertainty，is deeply and thoroughly studied on the basis of Bayesian statistics.First，the fundamental principles of Bayesian statistics are summarized.The statistical uncertainty in structural engineering is then modeled and analyzed by Bayesian updating approach.The various measures for structural statistical reliability are introduced.After that，two methods for statistical reliability analysis of structures considering statistical uncertainty are proposed to treat with the aleatory and epistemic uncertainties:the integrated approach and the separate approach.Two examples are given，one of which is a numerical one;the other is a fracture reliability problem.The examples demonstrate the influence of statistical uncertainty on the reliability indices of structures.

random reliability;statistical reliability;physical uncertainty;statistical uncertainty;Bayesian statistics

TK124

A

0367－6234(2011)08－0011－05

2010－04－03.

国家自然科学基金重大研究计划(90715021);

国家自然科学基金(50978080);

地震行业科研专项基金(200808073).

吕大刚(1970—)，男，教授，博士生导师;

王光远(1924—)，男，教授，中国工程院院士.

(编辑 赵丽莹)