基于贪心策略自动生成高区分度试卷的方法

杨超

（合肥学院 基础教学部，安徽 合肥 230601）

基于贪心策略自动生成高区分度试卷的方法

杨超

（合肥学院 基础教学部，安徽 合肥 230601）

建立了以生成高区分度试卷为目标的自动组卷问题的数学模型，针对该模型提出了基于贪心算法的试卷生成方法，将算法应用于实际的考试系统中，并与禁忌搜索算法生成试卷的策略进行比较，结果表明：贪心算法用更少的时间找到了更好的解.

试卷生成；贪心算法；区分度；禁忌搜索算法

随着信息科技的蓬勃发展，以计算机题库生成考卷的做法得到了广泛应用. 为了适应各类考试的需求，各种约束条件下的智能化考试抽题组卷研究取得了一些有效的研究成果[1-4]. 诸如招聘等类型的考试，需要有效拉开不同水平应试者的分数距离，这种情况下区分度在选题中显得尤为重要，现有的智能组卷算法虽能在保证区分度的同时兼顾试卷难度和知识覆盖面，但算法复杂，且由于抽题过程在“强约束”下，经常会出现无法满足性能要求的试卷（即约束问题变成了一个NP问题）. 本文弱化其中的部分约束条件，以获取最大平均区分度的试卷为组卷目标，设计了一种基于贪心策略的试卷生成算法.

1 问题定义

假设题库中题目数量为n，分别为Q1,Q2,…,Qn，题库涵盖了m个知识点C1,C2,…,Cm. 命题者在制作试卷时，要确定试卷内容涵盖的知识点和考试时间等约束条件，生成的试卷必须符合这些要求，且试卷中题目的平均区分度越大越好. 此组卷问题可以转化为组合最佳化问题[5]，定义为一个目标函数与一组考试约束条件的组合：

2 贪心算法设计

本文提出的贪心算法具体步骤描述如下.

1）初始化. 将题库中的题目依区分度由大到小排序，挑选前10%的题目为候选题库. 设置候选题库中题目的选中状态xi=0，试卷知识点相关度Rj与试卷答题时间T设为0.

2）计算试卷知识点相关度Rj与试卷答题时间T. 其中，

3）试题挑选阶段. 首先计算如果题目Qi加入试卷后，知识点相关度的误差值eRj与答题时间的误差值eT，计算公式如下：

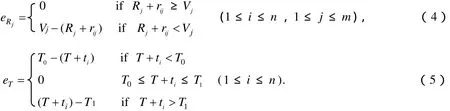
根据上面的计算结果，在没有被选中的题目中挑选使知识点和答题时间误差值总和最小的题目加入试卷，并将该题的选中状态xi设为1，同时检查试卷是否符合约束函数的要求，如果有一个条件满足则进行下一步骤，否则回到步骤2）继续添加试题.

4）修正阶段. 根据步骤3），当挑选的试题数达到试卷要求时停止选题，但此时很有可能没有满足约束条件（1）或（2），修正阶段是为了检查试卷的考察知识点和时间限制是否已经符合要求.如果不符合，则在候选题库中按照区分度从大到小的顺序选择xi=0的试题与试卷中的试题逐一进行交换，根据公式（4）和（5）计算两题交换后的误差值. 一般选择误差值递减最大的两题进行交换，直到误差值为0，即表示试卷满足所有约束条件.

5）优化阶段. 为了生成最大区分度的试卷，对已经初步完成的试卷进行优化. 即从候选题库和试卷中各挑选1题，若二者的区分度最大且试卷的知识点覆盖与时间限制都能符合要求，则将二者进行交换，直到无法从候选题库找到适合交换的题目，表示试卷已经不能再优化了，则贪心算法停止.

6）算法结束，生成试卷. 以上步骤结束后，所有在候选题库中xi=1的题目，即为贪心算法挑选的题目，导出即可得到目标试卷.

3 算法应用与分析

本文提出的试卷生成策略在“合肥学院基础部计算机文化基础无纸化考试系统”中得到应用，实验程序以JAVA技术实现，测试平台为个人计算机，CPU Intel CORE 2 DUO 3.0GHz、内存2G DDRIII，操作系统 Windows2000 server. 试题库平台为Microsoft SQL 2000，题库试题数从2 000到20 000题. 从题库中挑选题目生成试卷时，必须满足所有知识点相关度的下限，总答题时间介于90～120 min（即T0=90，T1=120）. 为了验证所提算法的有效性，在相同环境下我们还应用文献[7]提到的禁忌搜索算法生成试卷，并将二者进行比较，结果如表1所示.

表1 贪心算法和禁忌搜索算法生成试卷情况比较

由表1可知：贪心算法求解所需的计算时间均小于禁忌搜索算法；当题库数量2 000～4 000时，贪心算法求得的平均区分度比禁忌搜索算法稍差，但题库数量在5 000～20 000时，贪心算法所得的平均区分度比禁忌搜索算法理想. 此外，在贪心算法的设计中，首先需对题库的内容做筛选，即将区分度差的题目过滤，这样既能保证从题库中挑选的题目具有较好的区分度，又能节约大量的处理时间.

4 结束语

本文以生成高区分度试卷为目标，提出一个基于贪心算法的解决策略，并在实际中加以应用. 但本文定义的目标函数具有一定的局限性：在此目标函数下，只考虑题库中区分度好的题目，区分度较差的题目被选中的机率很少甚至没有，使区分度差的题目失去存在于题库的意义. 如果在此算法中出加入认知分类和难易度等因素，则可编制出更加精确的评价被测试者能力水平的试卷.

[1] 阎峰，安晓东. 基于粒子群优化算法的智能抽题策略研究[J]. 中北大学学报：自然科学版，2008, 29(4):333-337.

[2] 唐朝舜，董玉德，熊蓉. 在线随机组卷算法研究及实现[J]. 合肥工业大学学报：自然科学版，2006, 29(3): 296-299.

[3] 董敏，霍剑青，王晓蒲. 基于自适应遗传算法的智能组卷研究[J] .小型微型计算机系统，2004, 25(1): 82-85.

[4] 陈晓东，王宏宇. 一种基于改进遗传算法的组卷算法[J]. 哈尔滨工业大学学报，2005, 37(9): 1174-1176.

[5] 张爱文，樊红莲. 自适应遗传算法用于自动组卷中的数学模型设计[J]. 哈尔滨理工大学学报，2006, 11(5): 18-20.

[6] 董圣鸿，漆书青，戴海琦. 题目难度、区分度参数人工赋值方法的研究[J]. 考试研究，2005, 1(1): 25-32.

[7] HWANG Gwojen, YIN Pengyeng, YEH Shuheng. A tabu search approach to generating test sheets for multiple assessment criteria[J]. IEEE Transactions on Evolutionary Computation, 2006, 49(01): 89-97.

A Greedy Algorithm-based Method of High Discrimination Degree for Automatically Generating Test Papers

YANG Chao
(Department of Basic Sciences Teaching, Hefei University, Hefei 230601, China)

A mathematical model for automatic generating test papers with a high discrimination degree was designed. An automatic test paper generation method based on the greedy algorithm was proposed for the model. The algorithm was applied to the actual examination system. The experimental results showed that in most cases, the proposed greedy algorithm achieved a better solution in less time compared with the tabu search algorithm.

test paper generation; greedy algorithm; discrimination degree; tabu search algorithm

TP312

A

1006-7302（2011）01-0061-04

2010-09-17

杨超（1979—），男，讲师，硕士，安徽六安人，主要研究方向为计算机软件与理论.