CCD星点提取方法研究①

刘兴春，孙 浩

（65015部队，辽宁 大连116031）

0 引 言

美国的全球定位系统（GPS）虽然具有高精度的优势，但其最大的缺陷在于控制权在美国手中，在战时，这对于我们军事领域的导航无疑具有极大的制约［1]。惯性导航技术虽然精度较高、自主性很强，但其定位误差随时间积累的特性已成为制约其发展的瓶颈。卫星导航技术、无线电导航技术均存在着易受敌方电磁干扰等方面的缺陷。

天文导航作为最古老的导航定位技术之一，具有自主性、全天候性、经济性等方面的综合优势，现在各国都在加强天文导航技术的研究，提高其定位精度和速度，以满足现代导航定位的要求。随着现代科学技术的不断发展，天文导航正不断进行自我改造和完善，向着小型化、高精度、昼夜观测、全天候自动化导航和全球自主式导航方向发展［2]。天文导航的核心器件是星敏感器，随着天文导航和航天测控领域的要求不断提高，对星敏感器的性能提出了越来越高的要求。而CCD星点提取是星敏感器工作过程中的重要环节，因此，对其方法的研究具有非常重要的意义。

1 利用CCD实现天文测量的优点［1]

1.1 星敏感器工作原理

星敏感器又被称为星跟踪器，它的主要用途是确定运载体的姿态。

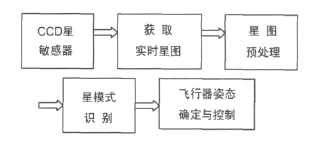
图1

星敏感器的工作原理是以恒星为参照物，利用CCD摄像机实拍到的星图，经过恒星检测、星图识别和姿态确定，计算出星敏感器瞄准线在惯性空间的瞬时指向，从而确定运载体的三轴绝对姿态。图1显示了基于自主式星敏感器的飞行器的姿态控制系统框图，从中可以看出，实现星点提取是进行姿态测量的关键一步［3]。

1.2 CCD天文定位的应用情况

由于CCD具有量子效率高、几何失真小、噪声低及实时采集和处理能力强的特点，从20世纪80年代初开始，世界上的天文望远镜纷纷用CCD代替照相底片（我国也在上世纪80年代后期开始给地面天文望远镜配备了CCD系统），使天文观测效率显著提高，可以说CCD技术是天文观测发展史上一个重要的里程碑。

1.3 CCD天文定位的优点

近年来CCD测量技术在天体测量中已有广泛的应用。应用表明，用CCD代替传统的照相底片，可获得比照相精度高几倍的星象位置。目前CCD技术已经基本发展成熟，今后其性能将进一步改善，结构更简单，感光芯片将有更多像素，感光面积更大，敏感度更高，黑暗噪音亦会降低。因此，将CCD数字摄影技术应用于天文测量，是当前国内外在天文定位方面的最新发展趋势［4]。

2 CCD图像中星点的提取方法

2.1 Moravec算子

针对点特征的提取的算子也有很多，Moravec算子就是其中很著名的算子之一。很多后来提出的点特征提取算子都是在它基础上进行改进得来的。

利用Moravec算子提取特征的原理：理论上，特征是影像灰度曲面上的不连续点。在实际影像中，由于点扩散函数的作用特征表现为在一个局部小区域内灰度的急剧变化或灰度分布的均匀性，也就是局部区域中具有较大的信息量。因此，可以以每个像元为中心，取一个n×n像素的窗口，计算窗口中的局部熵。若局部熵大于给定的阈值，则可以认为该像素即为一个特征。

如果不考虑噪声，实际影像是理想灰度函数与点扩散函数的卷积。其点特征灰度的分布均表现为从小到大或从大到小的明显变化，因此，除了用局部信息量来检测特征外，还可以利用特征提取算子对各个像素的某一大小的邻域窗口进行差分运算，选择其中的极值点或超过阈值的点作为特征点。正是基于以上思想，Moravec于1977年提出了利用灰度方差提取点特征的算子。首先。计算每个像元的兴趣值.即以该像元为中心，取一个W×W 的影像窗口。计算0°，45°，90°，135°四个方向的灰度差平方和，取其中最小值为该像元的兴趣值其次，根据实际影像设定一个阈值，遍历影像以兴趣值大于该阈值的点为候选点。最后，选一个一定大小的影像窗口.让该窗口遍历灰度图象，在此过程中取窗口中兴趣值最大的候选点为特征点，算法结束。

2.2 Förstner算子

Förstner算子是摄影测量中的著名点定位算子，其特点是速度快、精度较高。其基本思想是：对于角点，对最佳窗口内通过每个像元的边缘直线（垂直于梯度方向）进行加权中心化，得到角点的定位坐标；对于圆状点，对最佳窗口内通过每个像元的梯度直线进行加权中心化，得到圆心的坐标。因此，Förstner定位算子分两步进行。

1）最佳窗口。以每个像素为中心，取一个窗口N（如5×5）。计算每个窗口的有利值q和w.如果有利值大于给定的阈值，则将以该像元为中心的窗口作为候选最佳窗口，阈值为经验值，抑制局部非最大，得到最佳窗口。为了减少计算量，在计算q，w值之前，可以先计算像元：分别在x，y正反方向上的4个梯度值的绝对值，取出4个值中的最小值记为T，只有T值大于某个阈值时才计算q，w值。

2）定位和圆状点定位。最佳窗口内任意一个像元（r，c）的边缘直线l的方程为

式中：ρ为原点（设为最佳窗口的左上角像元）到直线l的距离；θ为梯度角；tgθ＝gc／gr，而gc，gr为该点的robert梯度。设角点坐标为（c0，r0），设v是点）到直线l的垂直距离，在）处给出误差方程

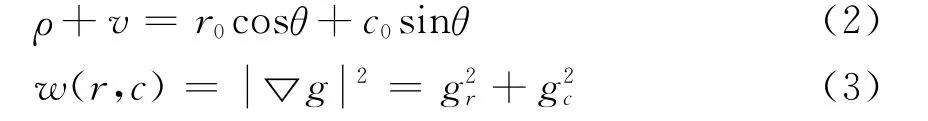
式（2）的含义是：把原点到边缘直线的距离ρ当作观测值，而保持边缘直线的方向不变，权w（r，c）等于梯度模的平方，所以权实质上是一个边缘尺度。

对式（3）法化，得到法方程

法化结果与最佳窗口内像元的加权中心化结果一致。对上式求解，可以得到角点坐标（c0，r0）。圆状点的定位与角点的定位是相似的。

2.3 Harris算子

通常都是用一个非负的二维函数f＝f（I），I＝（x，y）∈R2来表示一幅灰度图像。在特征点检测中，一直都用梯度（▽f＝（fx，fy）T）和梯度模（的概念来表征。在对图像进行特征提取之前，需要用一个满足≥0）的平滑函数去除图像的噪声点，以提高所提取特征点的有效性。高斯滤波器Gσ（x，y）＝exp［－（x2＋y2）／2σ2]／2πσ2（标准差σ＞0）通常作为这个平滑函数。用卷积g＊f代替f，完成平滑过程。根据Oergaard在对特征点和特征线性质的分析，可以得到以下结论：特征点都是大的点，但并非大 的点就是局部特征点，因为还存在边缘特征的情况，即，如果点I附近的所有点I′的梯度▽f（I′）都基本上是同一个方向的，表明I是一个在边缘上的点。只有同时满足：①是局部最大点；②点I附近的点I′的梯度▽f（I′）明显不同这两个条件时，才可以断定是特征点。

Harris算子原理是基于特征性质的分析，Harris和Stephens在H.Moravec工作的启发下，把求▽f（I）转化为矩阵形式的M（I）.这里M ＝M（I），I∈R2，M 定义为

2.4 改进Harris算子

从上面的两种方法的特点可以看出，Harris算子只用到一阶差分，计算简单，稳定性好，且不受阈值影响，可以最大限度地提出局部特征点，唯一不足的是精度不高。Förstner算子通过在最优窗口内进行加权中心化的操作，可以将定位精度提高到子像素，但它的缺点是要确定阈值，因此受图像灰度、对比度变化的影响。希望能集中两种常用方法的优点，提高点特征的提取效果。

改进的思路是：

首先利用Harris算子提取出一定数量的特征点，这些特征点都是图像局部范围内的最优点特征，每个特征点对应于一个具体的像素，因为它的精度只能达到一个像素。

然后用Harris算子提出的特征点作为Förstner的最佳窗口的中心点，在窗口内进行加权中心化操作，精确定位特征点的位置，将精度提高到子像素级别。

Harris算子编程实现起来简单，只需对图像进行一阶差分和卷积运算，这些都是图像处理中基础的算法。Harris算子提取的特征点准确，分布合理，用来作为Förstner的最佳窗口点很合适。但由于Harris算子需要对整幅影像进行差分和滤波处理，所以程序运行时花费的时间较多。为了提高执行的速度，可以在处理大图像时，首先将图像分成若干块，在每一块中分别提取一定数量的特征点，这样处理不但可以提高速度，还可以使特征点的分布较均匀。在利用Förstner算子时，由于不需要定位初始点，省去了设定阈值的工作，直接建立误差方程进行加权中心化，编程容易实现。

3 结 论

星敏感器对星空进行观测，得到模拟星图，通过星点获取，模式识别等一系列计算与导航星图进行匹配，最后得到星敏感器的姿态参数，通过已知的星敏感器与航天器、导弹、空间飞行器等的姿态关系来确定航天器、导弹、空间飞行器等的姿态以及方位，以实现它们的实时自主导航［5]。CCD星敏感器的关键问题是星图识别，星图识别就是从星敏感器获得的原始星图中获取星的位置和星等信息。

通过利用 Moravec算子、Förstner算子、Herris算子等几种点特征提取算子对图像处理，可以发现Harris算子只用到一阶差分，计算简单，稳定性好，且不受阈值影响，可以最大限度地提出局部特征点，而Förstner算子则是通过在最优窗口内进行加权中心化的操作，可以将定位精度提高到子像素，速度快，精度较高。但是Harris精度不高，而Förstner算子受图像灰度、对比度变化的影响。因此，本文又讨论了另一种算子——改进Harris算子，它融合了前两种算法的优点，大大提高了点特征的提取效果。

［1]许其凤.空间大地测量学［M].北京：解放军出版社，2001.

［2]李忠明.大地天文学［M].郑州：中国人民解放军测绘学院，1984.

［3]张 超.实用天文学讲义［M].郑州：中国人民解放军测绘学院，2003.

［4]张祖勋，张剑清.数字摄影测量学［M].郑州：中国人民解放军测绘学院，2006.

［5]郭 敏，张红英.CCD数字摄影在天文定位测量中的应用探讨［J].测绘技术装备，2005，7（1）：28－29.