GNSS-R反演海浪有效波高实验分析①
杨 尧,李明里,李伟强,杨东凯
(北京航空航天大学,北京100191)
0 引 言
海浪有效波高(SWH)是海况探测中的重要一项,在相关领域中起着重大作用。传统的探测有效波高的手段利用卫星高度计探测和高频地波雷达探测。
近年全球卫星定位系统(GNSS)发展迅速,不仅为用户提供了导航定位和精确授时信息,还提供了全天时不间断的L波段微波信号资源。研究表明,GNSS反射信号可应用于遥感应用。其技术原理是利用导航卫星L波段微波信号为发射源,通过航空或卫星平台上搭载的 GNSS-R(GNSS-Reflection)接收装置,全天时、全天候进行导航卫星直射及反射信号的同步接收,通过对直射和反射信号进行处理实现海洋要素微波遥感探测[1]。基于全球卫星定位系统的GNSS-R海洋微波遥感技术成为当前倍受关注的热点。
GNSS-R技术也可用于海浪波高探测。目前,基于GNSS-R技术的有效波高探测方法有两种。其一为利用海面回波信号的一维时延相关函数微分函数的探测方法[2]:由于海浪的存在,海洋表面粗糙,造成电磁波的漫反射,使得镜面反射得到的相关结果峰值上叠加了不同的延迟相关结果峰值,使最大的反射相关峰值后移,相关峰值的形状也发生了变化。回波功率的斜率随着海浪高度的分布而变化,因此,从DCF函数中可以得到海况信息。从DCF峰值的高度可以得到海面风速,从DCF函数的峰值点的码延迟位置可以得到海面平均高度,从DCF函数的宽度可以得到海面大浪的高度[3]。由于这种方法目前还没有具体实施方法,只是在理论上分析其可能性,因此,本文不作详细叙述。另一种方法是利用干涉复数场(ICF)测算海浪有效波高。本文对ICF方法进行分析讨论,并利用采集的数据对此方法进行分析。
1 利用干涉复数场测算有效波高
采用的接收机输出为直射和反射信号的复数时间序列,被称为零级数据。这个零级数据可以用于获得一级数据,如下面将要涉及的干涉复数场,信号的相关功率等,再利用一级数据就可以获得接收机与反射面高程差,有效波高,风速等二级数据。当然,软件接收机同时也能输出相应的导航信息,这里不详述。
1.1 干涉复数场
干涉复数场(ICF),是本文测量有效波高的重要信息。它定义如下[3-4]:在时间t时,干涉复数场为

其中,FD和FR分别表示直射和反射信号复数波形的最大幅度的复数值。
直射信号在这里用作一个参考信息,用来消除与海洋运动无关的项,例如一些残余多普勒频偏,导航比特相位偏移和直射信号功率变化以及绝大部分由电离层和中性大气引起的附加时间延迟对后续相关分析的影响。有效提高了测量海况信息的精度。ICF函数包含非常有价值的海况信息[3]。
相干积分滤掉了ICF函数的高频分量,在探测远海海况时需要考虑这一因素[3]。因为本文数据利用岸基接收机采集,所以不考虑该因素。
1.2 ICF的相关时间
需要重点讨论ICF函数的相关时间τF,定义ICF自相关函数的时间宽度Γ(Δ)[3-4]:
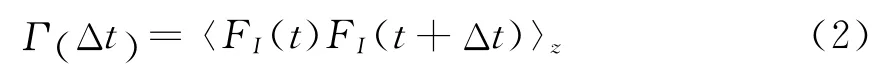
设海面高度为一个高斯概率分布,在这种情况下,相关时间和波浪方向无关。这样,ICF的相关时间可作为该高斯函数的二阶矩[3-4]:

可以看出,τF依赖于表面相关时间,有效波高的比值以及波长。
1.3 有效波高(SWH)反演模型
在远海海域,海浪可以充分成长,因此,可以根据海浪谱推导海面相关时间和SWH之间的关系式。Soulat等基于Elfouhaily等提出的统一海浪谱推导了τF和SWH 之间的关系式,是一个半经验公式,其反演精度为18cm[3]。假设表面相关时间是有效波高的函数,并定义有效相关时间为[3]

为了更准确的适应深海数据,引入SWH偏移参数SWH0和尺度参数γ,最终得到有效波高与有效相关时间的模型[3](SWH>SWH0时有效):
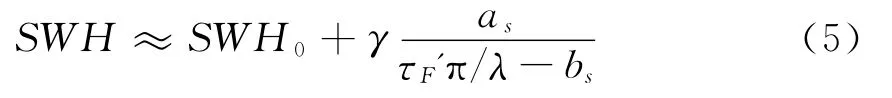
在风区不够长而且海床低的海域时,海浪不能充分成长,用海浪谱推导有效波高与相关时间之间的理论关系就很困难[5]。邵连军等人在论文[5]中提出了数据拟合的一个经验模型,该模型中同样使用了有效相关时间的概念[5],模型表达式为
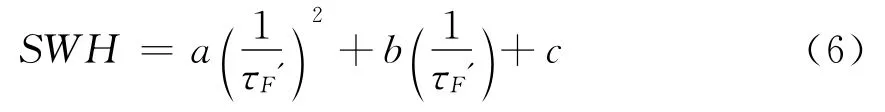
两个模型中的参数须根据具体测量区域情况和接收平台高度确定,为探索更为准确的测量方法利用所采集的数据对以上两个模型进行了分析比对。
1.4 误差分析
GPS卫星高度远远大于接收机高度,可以认为直射信号和反射信号经历同样的传播路径,但是反射波有一个附加路径,除此之外两种信号受到的电离层和中性大气折射的影响相等,这个反应在指数项上,通过干涉处理方法,可以基本达到消除共同传播路径的大气影响的目的[3,5]。反射波的附加路径上,接近海面的高度范围内,对流层折射指数较大,因此,它对信号的影响不应忽略。
2 实验结果分析
采用如图1所示的有效波高反演系统,采用的接收机输出为直射和反射信号的相关值复数序列,从输出中分别提取直射和反射信号幅度最大的相关值,得到干涉复数场ICF,求得干涉复数场的自相关函数,通过拟合得到连续的干涉复数场拟合函数并得到ICF的相干时间,求出有效相关时间,利用半经验模型计算获得有效波高值。整体过程如图1所示。
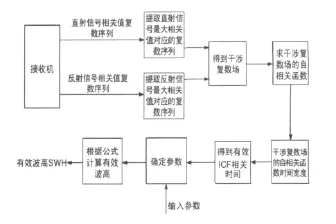
图1 利用干涉复数场有效波高反演系统
测定有效波高采用两个半经验模型,分别为F.Soulat等人在文献[3]中提出的半经验模型和邵连军等人在文献[5]中提到的半经验模型。为叙述方便,将其分别设为模型1,模型2。模型1中,有效波高SWH和有效ICF自相关时间宽度的关系模型如下[3]:

式中:as和bs分别为适应实际测量地点的参数;SWH 为有效波高;λ为信号波长;τF′为ICF自相关函数有效时间宽度。引入SWH 偏移参数SWH0和尺度参数γ.
因为不同的海域所适用的模型参数有差别,通过采集的数据确定了适用于本次实验地点的模型参数:
SWH0= -0.01,
as=3.50878,
bs=0.0842,
γ=1.8.
模型2中,同样使用了有效相关时间的概念,模型表达式为[5]
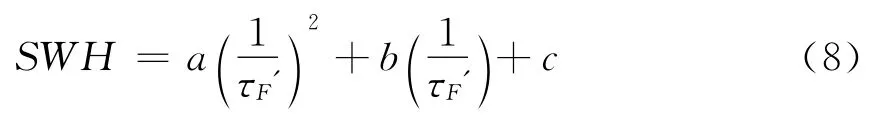
为了适应本论文采用数据的实际地点情况和接收平台高度情况,采用所采集数据确定模型参数:a=0.08,b=-0.073,c=0.5767。下面将对这两个模型进行验证。
在MATLAB环境下进行分析,创建图形用户界面如图2所示。

图2 海面有效波高测试系统用户界面
采用的数据为北航和气象局相关人员于2009年11月在博贺海洋气象科学实验基地采集的数据。采集数据的设备包括DDMR接收机,天线2个,电脑2台。对比数据采用WaMos海浪测波仪测定的有效波高,基础误差为0.5m.下面以13号卫星某时段的观测数据为例分析实验结果,该数据是10s的观测值,相关值为5组多普勒频移,每组55个码延迟。从13号卫星0多普勒频移组直射信号中选取1ms相关值,如图3所示;13号卫星直射信号和反射信号相关值幅度最大值波形分别如图4,图5所示;对应的干涉复数场波形如图6所示;干涉复数场自相关函数波形以及其拟合波形如图7所示。
在数据处理长度为10s,相干积分次数为10的情况下,得到ICF自相关函数如图7所示。
采用模型测算结果与对比数据比对结果如表1所示。
采集数据期间的有效波高与测波仪所测波高的最大偏差:
采用模型测算波高结果与对比数据对比图如图8所示。
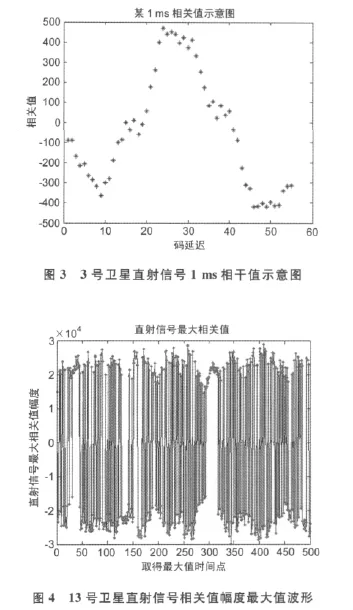
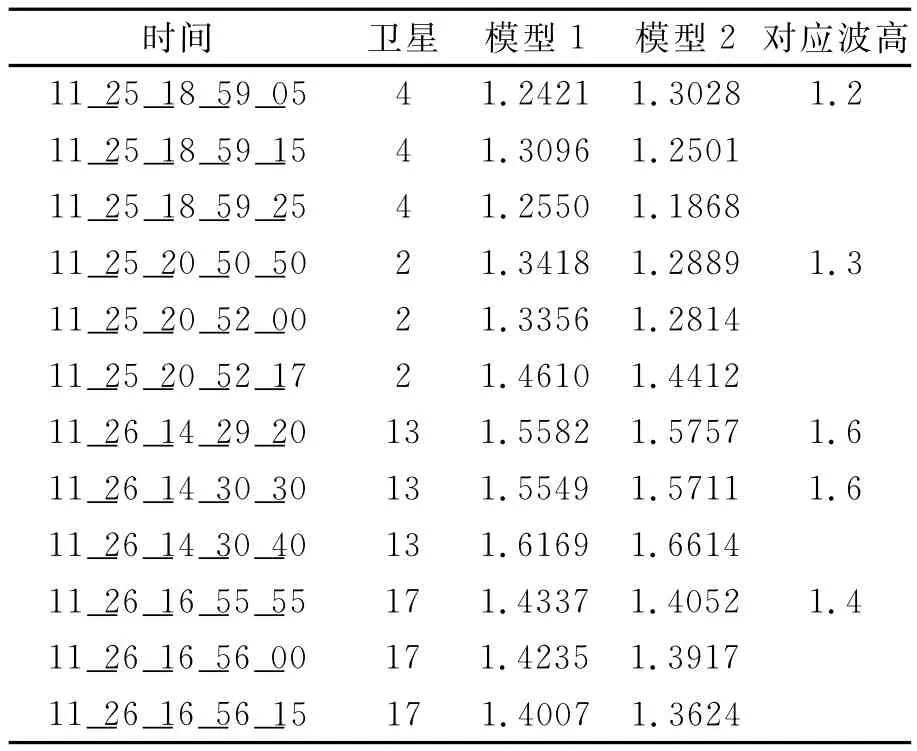
表1 测量结果与实测结果对比表


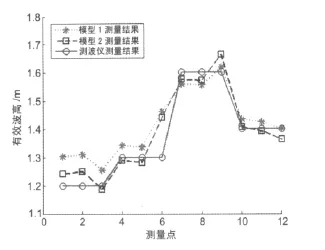
图8 有效波高测量结果对比图

式中:SWHn是本文模型测得的有效波高值,其中(n = 1,2);SWH 是利用测波仪测量的有效波高值;δi是每次计算的SWHn和SWH 之间差值,反映二者偏差大小;δmax和δmin是SWHn和SWH 之间最大和最小差值;δmean是SWHn和SWH 之间偏差的平均值,反映二者偏差的平均程度;D(δ)是δ的方差,反映δ的平稳程度。
使用示例数据的分析结果如表2所示。
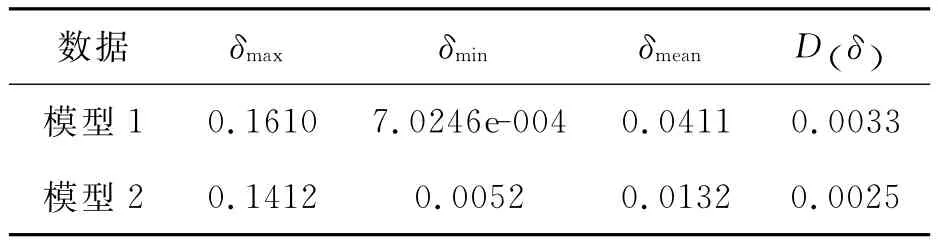
表2 有效波高测量分析数据表
由上述对比可以看出,本系统所测得的有效波高与测波仪测得的波高比较一致,模型2的平稳度和偏差的平均程度要好于模型1。
3 结 论
通过具体的分析和实现,本文基本达到了最初设定的低成本并简单有效地计算海洋有效波高的目标。应注意的是,数据处理参数可能对结果有所影响,在一段时间内有效波高可能变化较大,如果数据处理长度Ms过长,时间精确度将不能够达到要求造成有效波高测量不准确;但数据处理长度过短,有效波高没有变化,这样就浪费了计算时间和存储资源。因此,需要采用合适的数据处理长度。这种方法最大的优势是成本低,当然,此系统还存在一些缺点和不足,如采用的ICF和SWH之间的模型不够精准,并且是否可用于所有海域,还有待于进一步研究。
因本实验需要大量数据验证分析,但是由于现实条件有限未能得到足够的实验数据。需要说明的是,本实验采用的对比数据测得波高的时间分辨率不高,对结果分析时,认为对比数据短时间内的波高值相同,另外所采用的测波仪基础误差较大对结果的精度及参数确定产生了较大影响,有待于改善。
[1]张益强.基于GNSS反射信号的海洋微波遥感技术[D].北京:北京航空航天大学,2008.
[2]Hajj G A,Zuffada C.Theoretical description of a bistatic system for ocean altimetry using the GPS signals[J].Radio Science,2003,38(5):1089-1107.
[3]Soulat F,Caparrini M,Germain O,et al.Sea state monitoring using coastal GNSS-R [J].Geophysical Research Letters,2004,31(21):303-307.
[4]Ruffini G,Soulat F.On the GNSS-R interferometric complex field coherence time [EB/OL].(2004-06-21).http://arXiv.org/abs/physics/0406084v2.
[5]邵连军,张训械,王 鑫 ,等.利用GNSS-R信号反演海浪波高 [J].武汉:武汉大学学报·信息科学版,2008,33(5):1671-8860.

