基于小波变换的遥感图像压缩①
郭广杰,张 静,郭海生
(1.河南省舞钢市建设局,河南 舞钢462500;2.信息工程大学测绘学院,河南 郑州450052;3.河南省灵宝市国土资源局,河南 灵宝472501)
0 引 言
遥感数据的大信息量、大容量和越来越高的分辨率对图像的存储和传输提出了更高的要求,因此有效的图像压缩就显得特别重要。小波变换是发展起来的可以对信号进行多尺度分析的工具,由于其具有良好的时频局部化特性,在图像处理领域也得到了广泛的应用,尤其在图像压缩编码方面取得了比较好的效果。小波基也有无穷多组,用不同的小波基函数对信号进行小波变换和压缩编码,得到的结果是不同的。当然并不是所有的小波基适合于图像的压缩编码,这就要求根据不同小波基性质与图像压缩编码特点的对应关系,有针对性的选择适合的小波基进行图像压缩。
而小波基的选择又直接决定了图像压缩的压缩效果和压缩速度。
1 小波变换基础
小波函数的定义[1-2]为:设φ(t)为一平方可积函数,即φ(t)∈L2(R),若其傅立叶变换Ψ(w)满足条件


称φa,b(t)为依赖于参数a,b的小波基函数,式中:a为伸缩因子或尺度因子,将基本小波伸缩;b为平移因子,将基本小波作位移。
对于任意的函数或者信号f(t)∈L2(R),用小波函数集 {φa,b(t)}进行分解运算,其连续小波变换为

已经证明,如果采用的小波满足可容性条件式(1),则其逆变换存在,即根据信号的小波变换系数可以精确地恢复原始信号,其逆变换(重构)公式为
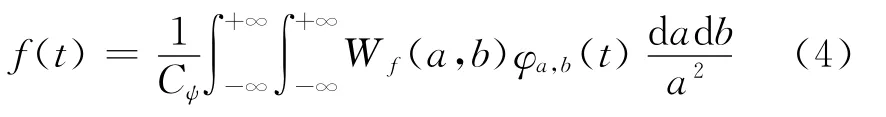
而图像是二维信号,因此,需将小波变换由一维推广到二维,离散栅格上二维小波变换的定义为[3]
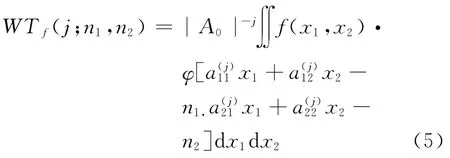
2 常用小波基的特性
目前比较常用的有 Haar、Daubechies、Mexican和Morlet等用于图像压缩的小波基,根据其正交性、双正交性、紧支撑性和连续小波变换等性质将其总结如表1所示[4]。

表1 常用小波的主要特征
3 小波基性质与图像压缩的关系
将小波变换引入到图像压缩编码的领域中,特别是对于遥感图像来说,小波函数的正交性、紧支性、线性相位性、对称性、正则性等性质与图像的压缩质量、速度、压缩比有密切的关系。首先要考虑的是小波基的选择,表2列举了小波基的主要性质对遥感影像压缩比、压缩速度和压缩质量的影响。

表2 小波基性质对遥感影像压缩的关系
正则性比较好的小波函数虽然可以提高图像的压缩质量,但是压缩的速度也相应下降了,具有对称性的小波可以实现图像的无损压缩。
4 部分小波基的图像压缩性比较和实验
Coiflet、Symlets和 Haar都是Daubechies小波系的推广,在实际应用中,Daubechies由于其良好的与图像压缩密切的正交性、紧支性和正则性,在静态图像中得到了很好的应用。由于图像的重建效果随正则性的增加而改善,正则性随滤波器的增加而增加,但滤波器不能太长,否则会因计算量太大没有实际应用价值。选择Db2,Db4,Db6,Db8,Db10进行试验,其部分小波函数和尺度函数图如图1所示,基本性质如表3所示[5]
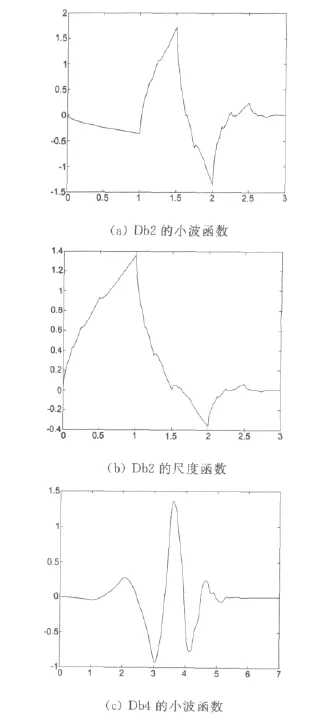

图1 Db部分小波函数和尺度函数

表3 部分Db小波的性质参数
峰值信噪比PSNR是图像重构质量的衡量标准,小波分解和重构时间长短是图像压缩效率的表现,在这里我们取两者作为不同的小波性能的参数。基于MATLAB6.5为平台对图2三级分解,对变换后的系数不进行量化和编码,只将系数简单取整,将高频部分舍去,用低频小波系数进行图像重构,实验的结果如表4所示。

图2 实验图像

表4 小波基的性能比较
5 结 论
根据以上实验的结果和其它的相关研究,可以得出在图像压缩方面小波基选择的经验和原则
1)正则性越好,得到的PSNR越高,即压缩后重建的图像质量越高,但是耗费的时间越多,压缩效率不高。
2)目前,Daubechies小波是最常用的紧支性小波,应用精度比较高,与小波变换的时间联系密切,紧支性越好,耗费的时间就越少,效率就越高。
3)几乎所有的正交小波(除了Haar小波基),不存在对称的紧支性正交小波,但是双正交小波基可以合成对称的紧支撑小波基,能减少重建图像的边缘失真,因此,我们尽量选择对称的小波基。
4)消失矩阶数越大,图像越能有效的检测出图像的奇异点,提高图像的压缩质量和压缩比,所以我们选择的小波基必须有足够高的消失矩。
[1]彭玉华.小波变换与工程应用[M].北京:测绘出版社,2002(1):13-15.
[2]徐佩霞,孙功宪.小波分析与应用实例[M].合肥:中国科学技术出版社,2001(1):31-44.
[3]杨福生.小波变换的工程分析与应用[M].北京:科学出版社,1999:112-114.
[4]姜凤娇.基于小波零树编码的遥感图像压缩研究[D].大连:大连海事大学.2006:18-19.
[5]柯 丽.基于小波变换的空间遥感图像实时压缩方法研究[D].长春:中国科学院长春光学精密机械与物理研究所博士论文,2004:8-14.

