小型低水头坝围堰拆除设计的流量频率分布选择

L.A.可汗

1 概 述

拆除水坝正日益成为与解决水坝老化相关的安全与环境问题的一个可接受的方案。由于很多水坝接近其使用寿命,小型低水头水坝的退役预计会继续进行。

拆坝前的重要一步是修建一个围堰以便使拆除活动有序进行。影响围堰建设费用的最重要因素之一就是其高度,它是由拆除期预计的最大河流流量所确定的。已经或正在考虑拆除的坝多是小型或低水头坝,因此,拆除工作需要的时间一般是几个月。为尽可能降低围堰高度和减少建设费用,水坝拆除一般在 1 a中枯水季节进行。

水坝拆除期间可能最大流量采用河流流量数据的水文频率分析法估计。通常,水坝的水文设计是基于年最大或可能最大洪水的分析。基于年最大流量设计的围堰(只在 1 a低水期的几个月内挡水)可能非常高。对于这种情况,利用代表水坝拆除期(不是全年)的流量进行设计是比较适宜的。

本项研究的重点是常年性河流上的水坝拆除,最小实测流量一般比测量临界值要高。本文假定极端事件的概率分布函数(P D F)可用于拆坝期的最大流量系列,这个时候河流流量比年最大流量要小很多,但比年最小流量要大很多。这个假设是基于对将极端事件(年最大和最小流量)的 P D F用于年平均流量、7 d平均流量以及最大月均流量所进行的观测。接着,将极端事件的 P D F与按月分组的数据用来分析降雨数据。

在美国,对数皮尔逊Ⅲ型是推荐的 PDF,可用来分析常年性河流的实测季流量和月流量。然而,对不同数据类别(年平均值和最小值;月、季最大值或最小值),对数皮尔逊Ⅲ型是否是最适合的 P D F尚不清楚。一般来说,伽玛分布也是比较适合估计河流年均流量的分布形式。

本文主要目的在于识别建立洪水流量频率曲线所需采用的 PDF,以设计一座用于马莫特坝拆除的围堰。在一个水文年的低水月份中考虑了 4种拆坝期:1个月期限(8月),2个月期限(8～9月),3个月期限(7～9月),4个月期限(7～10月)。对每种期限,分析日均和时均(瞬时)流量系列以确定它们是否服从同样的 P D F。接着,还利用日均流量数据研究了样本大小(15 a和 50 a)对估计的流量的影响。较小的样本大小对应的是时均流量数据的记录长度。

共研究了 9种 P D F,根据参数个数将它们分为两组。第 1组由 4个两参数的 PDF组成:对数(正态 LN 2)、威布 (W2)、广义派尔托 (G P 2)、伽马(GAM)。第 2组的三参数 P D F是广义极值(G E V)、对数正态(L N 3)、广义派尔托 (G P 3)、皮尔逊Ⅲ型(P 3)、对数 -皮尔逊Ⅲ型(L P 3)。利用 L-矩比率图进行时均和日均数据的分析,以识别合适的 P D F。被识别的 P D F的适用性是通过概率图的相关系数(P P C C)进行验证的。然后用选定的 P D F来估计围堰的设计流量。由于低水头坝的拆除还会继续,本文提出的方法将有利于获得经济且成本合理的围堰设计方案。

2 频率分析方法

水文频率分析的两个可能目标是选择一个合适的 P D F和建立流量频率曲线。本文采用基于 L-矩的方法进行分析,然后通过计算 P P C C来验证这种分析。L-矩估值比传统的乘积矩更为可取。因它们对于小样本及所有的概率分布基本上是无偏的。

本文中分析必须用到的一个概率分布的前 4个L-矩给定如下:

式中 βr(r=0,1,2,3)代表概率加权矩(P WM)。定义为:

式中 F(X)是随机变量 X累积分布函数,当 r=0,第1个 L矩等于该分布的均值。而且,λ2,λ3,λ4分别是分布的比率、偏斜度、峭度。实际上 P WM是根据一个有限样本估计的,无偏的 P WM估值由下式给出:

式中 n是样本大小,{x(j)}是有序观测值,使 X(1)≥X(2)≥…X(n)。将公式(3)给出的 βr的无偏样本估值代入公式(1)中可得到 L-矩 λr的样本估值 lγ。类似于乘积矩比率(变异系数、偏斜度、峭度),L-矩比率由下列公式确定:

将这些比率点绘在图中得到 L-矩比率图,以识别一个描述数据集的合适分布,因为对每个 P D F,L-矩比率中有着明显的关系。 τ2与 τ3和 τ4与 τ3图分别用来选择二参数和三参数的 P D F。在式(4)中用 λr各自的样本估值 lr代替 λr的比得出 L-矩比率的样本估值。

对于某个 P D F,如果能得到 C D F的理论方程(接近的形式),就可以建立 τ2,τ3和 τ4之间的理论关系。本文用建议的方程,直接使用 L P 3的理论 L-矩比率图。以前的研究将对数转换的数据与 P 3分布的 L-矩比率进行对比。表 1总结了本文中与P D F的 τ2,τ3和 τ4有关的多项式近似式。表 2列出了 L P 3的多项式表达式的系数。

表1 不同概率分布构造线性距比率图的多项式表达式

表2 将 τ3和τ4关联作为偏斜度函数方程系数的对数皮尔逊Ⅲ型分布

3 河流现场流量数据

马莫特坝在俄亥俄州桑迪河上,距波特兰市 48 k m,2007年 10月曾经决口。它是桑迪河上最上游的径流式水坝(水库库容可以忽略)。因此,可以认为工程现场的河流流量是没有受到调节的。

从美国地质调查局(U S G S)第 14137000站获得了 1911～2002年和 1988～2002年的日均和时均流量数据。该站控制了桑迪河 690 k m2的流域面积,位于该坝上游0.5 k m。由于 1988～2002年时均流量数据集很大,U S G S提供了除了 2002水文年以外的 7～10月的数据,通过比较河流日均流量和时均流量水文过程线获得 2002水文年完整数据集(图1)。日均流量数据的检查表明 1950年前常有数据缺失,因此,采用 1953～2002年日均数据进行分析。时均数据在高水月份(12～4月)存在更长时间的数据缺失 。幸运的是 7～10月的时均数据只有比较少的(短的间隔)数据缺失。因此,采用样条插值来填补缺失数据。

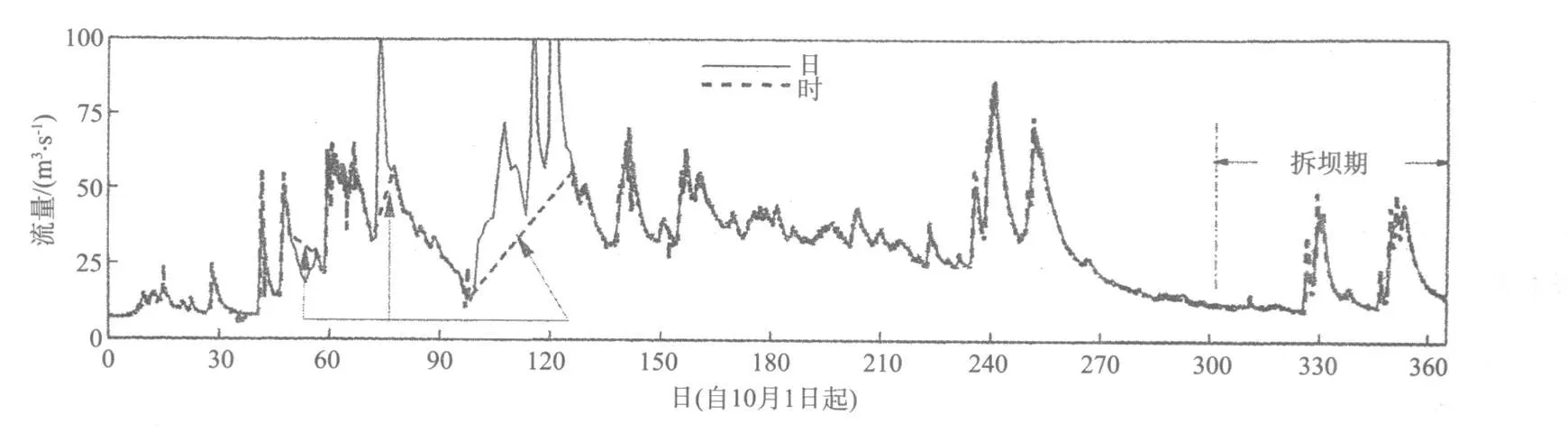
图 1 俄亥俄州马莫特坝附近桑迪河的 2002水文年日均、时均的水文过程线比较

在 2003年的 U S G S报告中可发现工程现场的年、月、日平均流量的统计分析。洪水流量最大值发生在 1964年 12月,最高实测瞬时流量为 1740 m3/s,其最大日均流量为 1172 m3/s。一般来说,7～10月河流流量较小。7～10月最高实测日均流量分别为 39.218.8、29.9、61.4 m3/s。相应地最小实测日均流量为9.9、7.8、7.1、7.8 m3/s。该测站最低实测日均流量为5.47 m3/s。根据 1912～2003年的数据,最高和最低日均流量分别发生在 12月和 8月。因此,最合适的大坝拆除期应该集中在 8月。值得注意的是 2002水文年出现了非典型的情况,10月份的流量比 9月份的流量小。一般来说,10月最大流量要显著高于 9月份的值。1988～2002年,10月的时均最大流量在12.8～712.2 m3/s之间变化,而 9月份的相应流量在10.6～41.3 m3/s之间变化。

4 结果与分析

除了年最大日流量洪水系列(D A M X)以外,本文河流流量分析并不代表通常意义的极值。然而,它代表拆坝期的极值。例如,当考虑 2个月的拆坝期,8～9月的最大流量就假定代表极值。对每种拆坝期,日均记录都有样本大小为 50(D A 50;1953～2002年)和 15(D A 15;1988～2002年)的两个流量系列。由于可用的时均数据取自 1988～2002年,考虑了与拆坝期对应的 4个流量系列(H A 15)。同时分析了时均与日均流量系列,以确定二者是否有同样的频率分布。不同样本大小的日均流量数据分析,是为了了解在工程现场流量变化情况时小样本记录的充分性。

图 2比较了 4个二参数 P D F(L N 2,W2,G P 2和G A M)的 L-C v对 L-偏斜度估计与其理论关系。为表达方便,假定采用同一 P D F来估计不同拆坝期的流量,用 D A 50,D A 15或 H A 15(除了 D A M X)代表的每一组都有 4个数据点(L-矩的比率)。D A M X洪水系列有一组 L-矩比率。图 3比较了三参数P D F(L P 3除外)的 L-峭度估值与 L-偏斜度估值。L P 3的 L-峭度与 L-偏斜度之间的理论关系是偏斜度的函数,是偏斜度在 -1.4～1.4之间(对数空间)变化的一条包络曲线,如图 4所示。

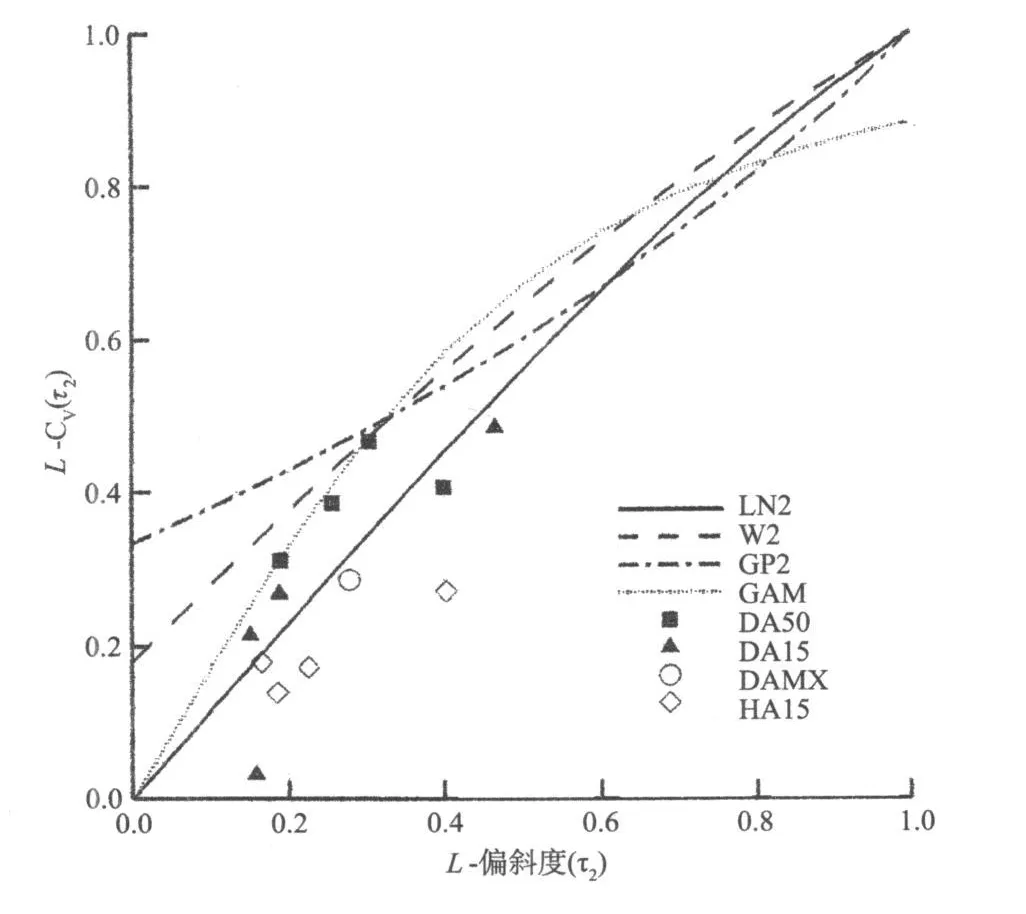
图 2 L-变异系数(τ2)-L-偏斜度(τ3)与相应的两参数频率分布函数比率对比的L-矩比率图

图 3 L-峭度(τ4)-L-偏斜度(τ3)与相应的三参数频率分布函数(除对数皮尔逊Ⅲ型分布以外)对比的L-矩比率图

图 4 L-峭度(τ4)-L-偏斜度(τ3)与相应的三参数对数皮尔逊Ⅲ型分布频率分布函数对比的L-矩比率图

从图 2可知,二参数 G A M和 L N 2是代表工程现场数据的两种可能 P D F。然而,从图 3和图 4中不能类似地识别三参数的 P D F。为有助于在这种情况下选择一种 P D F,已建议采用不同的分析方法。概念上它们代表了样本与 P D F之间距离的测度。由于本文是分析现场数据,拟合优度的合适测度是样本和 P D F之间的最小距离 δ。对于三参数 P D F,距离 δ可以如下表示:

本文中,δ是用一维黄金分割法确定的。二参数P D F的相应方程可以通过用(τ2,τ3)代替(τ3,τ4),并用(t2,t3)代替(t3,t4)得到。对于 L P 3分布,采用与每个样本的对数偏斜度(-0.49～1.47)对应的 L-矩峭度(τ4)与 L-偏斜度(τ3)关系曲线来确定 δ(不是图 4中的包络曲线)。表 3给出了不同P D F的样本(50 a日均流量、15 a日均流量、15 a时均、50 a年最大流量系列)的最小距离。除了年最大系列以外,表中给出了算术平均值(基于 4个拆坝期)。在两参数的 P D F中,最好的 P D F是 L N 2,其次是 G A M。前者也是 50 a年最大流量系列的最好P D F。使用三参数 P D F时,同样的数据系列似乎也可用 G E V最好地表示。如果只选择一个三参数P D F,则 L N 3是最好的选择。然而,由于 L N 3和 L P 3的 δ差别不大,所以也可以采用 L P 3分布。即使是年最大流量系列,L N 3比 L P 3表现要略微好点。

表3 公式(5)定义的 9种P D F的样本最小距离δ(δ越小表示该概率分布越与样本相匹配)

为独立验证 L N 2、L N 3、L P 3是代表现场数据的可接受的 P D F,采用数据的对数与威布点位置公式对比来计算概率图相关系数 P P C C(表 4)。如果计算得出的 P P C C值比临界值大,允许其分布在某一规定的显著性水平上代表该数据。对于正态分布或L N 2和 L N 3的数据的对数,置信区间为 5%的临界值列在表 4中最后一列。这些临界值是本文中样本大小(15,50)的函数。P 3分布(或 L P 3分布的数据的对数值)的临界值是样本大小及偏斜度的函数,列在表 4倒数第 2列。这些计算的 P P C C的值变化不大,因为 L-矩分析已经将相关系数较小的 P D F筛选出去。表 4表明可采用 L N 3或 L P 3分布来估计 5%置信区间的流量。然而,与基于 L-矩比率的结论相反,在样本大小从 15增大到 50时,L N 2分布可能不适合。这个结论是基于观察到 P P C C值比 3个拆坝期(8月份,8～9月份,7～9月份)的临界值低。

表3和表 4中信息表明,L N 2,L N 3和 L P 3可用来估计围堰的设计流量。L N 2和 L N 3之间的主要差别在于从 L N 3的数据中减去了下界。下界估计量 δ用下式表示:

式中 xmedian是样本的中值,并且 x(1)+x(n)-2xmedian。如果 x(1)+x(n)-2xmedian＜0,那么公式 6提供了上界,表明 ln(ξ-x)成正态分布。图 5～8示出了用 3个选择的 P D F绘制的 4个拆坝期的流量频率曲线区间。图 9是基于年最大流量系列的相应流量频率曲线。这些图也指出了 90%的置信区间[Q(+5%)和 Q(-5%)]。

表4 不同拆坝期的3种选定频率分布的P P C C及 5%显著性水平的临界值

管理机构(如联邦紧急管理机构、联邦能源与管理委员会、美国工程师兵团)并没有对拆除一座小型低水坝的施工围堰设计直接规定洪水重现期。图 5～9列出了直到 15 a重现期的流量频率曲线。

假定 5 a重现期对于围堰设计是合适的,图 5～8以及表 5表明选择的 P D F(L N 2、L N 3、L P 3)提供了接近于设计流量的合理估值。值得注意的是,表 5中估计流量的差异比按其他重现期估计的要小。因为许多 P D F在 5 a重现期附近是相互交叉的。然而,所有的流量估值都是在 90%的置信区间以内。除非超过 3个月的拆坝期,否则基于 1988～2002年的时均与日均流量数据估计的设计流量的差异会小于 25%。对于 4个月的拆坝期,任何基于时均数据的估值都比基于日均流量的估值至少高 50%。一般来说,样本容量增大,数据的可变性(用标准差表示 )也增大。从图5～8及表5可以看出 ,如果拆坝期小于 4个月,设计流量随着样本尺寸增大而增大。然而,对于 4个月的拆坝期,基于较短流量记录(日均、时均流量系列)的估值要高些。

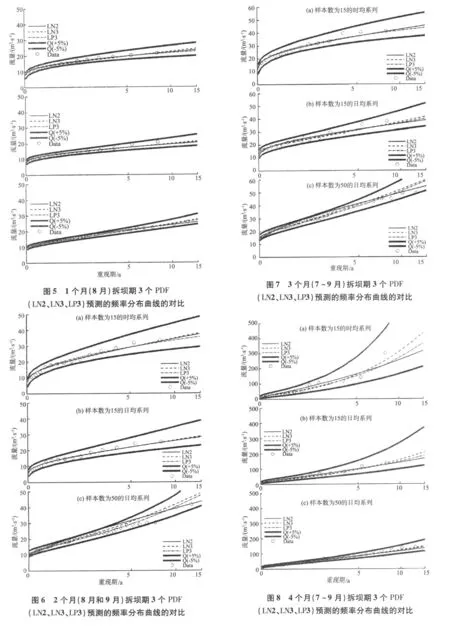
图 950 a年最大洪峰流量系列的 3种概率分布(L N2、L N 3、L P 3)估计的流量频率分布曲线

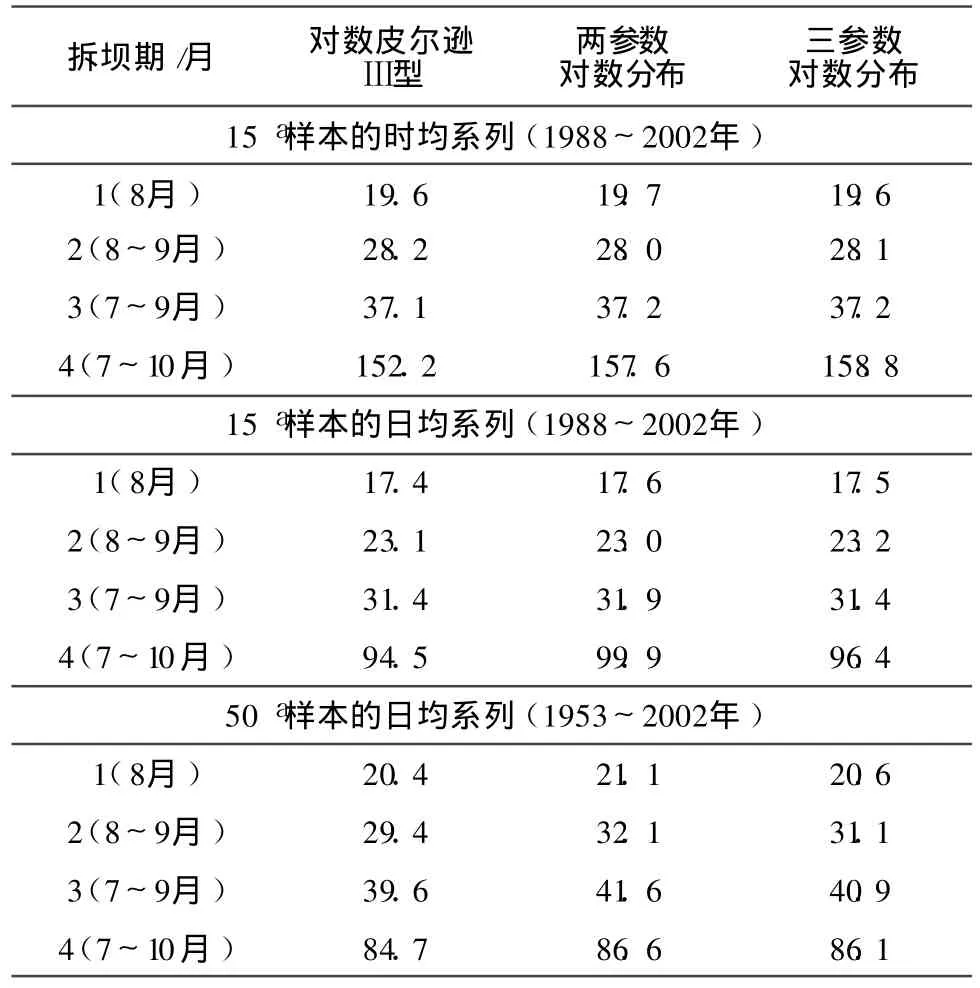
表5 用 3种概率分布估计的 5a重现期设计流量的对比

对于 3个和 4个月拆坝期,基于时均数据的设计流量分别为37.2 m3/s(L N 2、L N 3)和158.8 m3/s(L N 3)。增加 1个月拆除时间设计流量将增至4.25倍。因此,从水文角度考虑,最优的拆坝期似乎约为3个月。实际时间期限会受到其他因素的影响,包括工程管理、运行、施工。基于年最大流量系列估计的相应流量为496.4 m3/s。这个估值为 3个月拆坝期设计流量的13.33倍。因此,基于年最大流量系列选择围堰的高度会得出一个昂贵的、不经济的设计方案。

5 结 语

小型水坝拆除的围堰费用有效设计应该基于拆坝期的河流流量信息,而不是全年的流量信息。因此,本文考虑 7～10月份低水期内 4个可能的拆坝期。本文利用的现场数据代表 1988～2002年时均流量,1953～2002年日均流量。日均流量分为 15 a和 50 a的样本。前者 15 a日均流量样本,与时均数据系列相对应,说明了不同时长的流量平均期的影响。

将河流流量数据限制在拆坝期间,意味着最大流量系列不再是通常意义的极值。然而它们代表的是拆坝期的极值事件。假定可以应用年最大和最小流量系列的 P D F,分析了 4个二参数的 P D F和 5个三参数的 P D F。通过对比样本的 L-矩比率与相应的 P D F曲线,合适 P D F的个数减少到 3个。为了进一步独立证实选择的 P D F的合适性,计算了 L N 2、L N 3、L P 3的 P P C C。结果表明 L N 3、L P 3可以用来估计设计流量。一般来说,同样的 P D F可以用于现场的时均和日均流量数据。

拆坝期小于 4个月(7～9月)的数据分析表明,根据时均流量系列估计的设计流量都在根据日均流量系列估计值的 90%置信区间之内。如果拆坝期限延长到 10月,相应设计流量(基于时均数据系列)要高 50%左右。无论哪种情况(时均或日均),4个月拆坝期设计流量大概是 3个月拆坝期的设计流量的 3倍。因此,工程现场最优拆坝期约为 3个月。因此,用基于拆坝期的数据来估计设计流量可望得出一个费用合理的围堰设计方案。

为拆除小型低水头坝使围堰设计方案经济适用的方法是工程上一个重要的考虑方面。然而值得注意的是,拆除较大的坝用基于年最大流量系列估计设计流量是比较合适的。如华盛顿州的 33 m高的艾尔瓦(E l w h a)坝和 64 m高的格莱因斯卡因(G l in e C a n y o n)坝。