砂砾过滤介质的处理效果对雨水渗透系统设计与运用的意义

[澳大利亚] B.E.哈特等

1 概 述

雨水渗透系统是一种应对暴雨径流的技术手段,在欧洲应用尤其广泛。该技术可用于削减暴雨径流量,并能将受纳水体的污染物总量降至最低。雨水渗透系统可采用的构造形式很多,最典型的是在浅沟或浅池中填充砂砾过滤介质的构造。2004年美国环保署发现,虽然吸附和微生物摄取等化学生物过程在某种程度上可对污染物的去除起到一定的作用,但在渗透系统中大部分污染物是通过机械和物理化学作用过滤去除的。雨水可通过系统渗出后流入周围土壤,或由下水道收集后输送到受纳水体,前者最为常见。

尽管多数渗透系统由于阻塞等原因以失败告终,但研究报告表明,在要求设置沉砂设施之前,已设计出雨水渗透系统,并已运行了20多年。传统的雨水渗透系统并非用于去除污染物质,其主要目的是削减暴雨径流量,从而使进入受纳水体的污染负荷得以减少。尽管如此,人们仍未充分了解雨水渗透系统在空间(沿滤层深度剖面)和时间上的去污效果,尤其是当阻塞发生时。许多研究仅仅只呈现渗透系统性能的一个方面,很少针对系统水力和水质方面的处理效果做出实验评估。当提及污染物的去除时,研究结果往往不一致,如何处理渗透系统中长期积累的污染物也尚未确定。

如果雨水渗透系统得以广泛应用,其长期拦污效果则是研究的一个重要领域。渗透系统中污染物的空间分布有助于评估周围土壤和地下水受到污染风险的程度,同时,系统性能随时间变化可以显示系统在保护受纳水体不受城市暴雨径流影响方面的有效性问题。本文介绍了传统渗透系统对雨水处理效果的实验室研究结果,以期对大量砂砾渗透系统(如渗渠、渗透池、渗水坑及盲沟)的设计进行改进,内容涉及深度、水力负荷率等参数,以及这些系统应对雨水中不同污染物的适用性。

2 实验材料与方法

为了模拟砂砾渗透系统的长期运行特征,实验人员用砂砾介质建造了一个垂直圆柱体,并在其上多次进行模拟暴雨径流和污染物荷载实验。每次实验都使圆柱体保持运行状态直到被阻塞为止,重建后再开始下一次实验。每次模拟实验都会对水压和水质进行全程测量。

2.1 资料收集

2.1.1 半人工暴雨

2006年,研究人员黛莉缇克和弗莱彻分析称,在实验室模拟真实的暴雨污染特征,可采用“天然”或“人工”降雨,二者均有利弊。利用天然雨水(即从下水道排出口收集到的雨水)的优点在于其物理、生物、化学特性均能如实反映雨水的实际情况。但很难保持样本浓度和其他特征(如沉积物颗粒粒径分布)的稳定性,可能将输入雨水的人为改变因素引入系统处理测量效果。而利用人造雨水(即采用实验室化学制剂配制的雨水)能够获得更好的稳定性,但同时也会因其中的非天然成分产生假象,缺乏真实性。

因此,实验人员采取了折衷方案应对该问题,即从一个雨水塘中获取泥沙沉积物以制备雨水。基于邓肯在全球范围内对雨水水质的研究成果,确定出适用的典型暴雨下污染物浓度,如下所示:总悬浮固体(TSS)150 mg/L,总氮(TN)2.6 mg/L,总磷(TP)0.35 mg/L,铜离子(Cu)0.05 mg/L,铅离子(Pb)0.14 mg/L,以及锌离子(Zn)0.25 mg/L。

2005年,研究人员阿尔戈和佩扎尼缇在确定投入渗透系统的泥沙数目和粒径时,假定粒径较大(＞300 μ m)的粗砂已在预处理措施中去除。在装有550 L自来水的水池中加入粒径 ＜300 μ m给定质量的泥沙,以配制与高度城市化地区径流相似的悬浮固体浓度。该方法能在较大程度上获取所需的营养物和重金属浓度,且可通过添加实验室化学制剂加以补足。这种半人工雨水的恒定均一状态是通过在入流水池中通入高速的气泡,形成循环旋流效果得到的。

2.1.2 实验装备

2007年,研究人员锡瑞瓦尔登等人做了一项实验,将常用于雨水渗透系统中的砂砾介质(平均粒径10.5 mm)填入一个内径20 cm、高90 cm的有机玻璃圆柱体内(见图1),在一个70 cm厚的细砂层上放置砂砾,该细砂层渗透系数为120 mm/h(2.4×10-5m/s),与渗透系统周围常见的砂质壤土的水力特性近似。砂砾层的孔隙率大约为0.45,空隙体积为12.7 L。压力传感器(集成电路原件,型号 86 psi)每隔20 cm从侧面植入圆柱体,沿圆柱体通长布置(包括砂砾层与细砂层),这些插入点同时也作为水样的取样点。该实验装置采用一维模型对渗透系统进行模拟(注:此处不考虑侧向渗透介质及周围土壤的影响)。

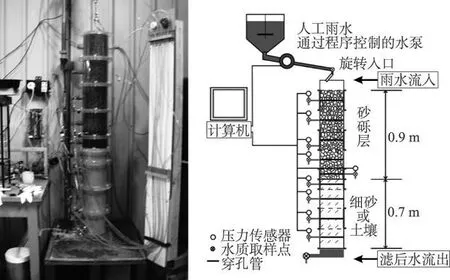
图1 实验用的砂砾渗透圆柱体的照片与示意

雨水通过一个旋转喷水装置,导入砂砾过滤介质,其中导入速率由软件和压力传感器控制。而流出渗透系统的雨水则通过一个精度为0.2 mm的倾卸斗雨量计进行监控。

实验装置由多个可装配部件组成。每次实验结束后,需将实验装置仔细拆卸开。将每节部件中的砂砾层烘干后称重,然后彻底清洗,再次烘干进行称重。夹带着泥沙的砾石与冲洗干净的砾石称重结果的差值即为泥沙沉积物的重量。聚集在过滤装置每节内的泥沙沉积物质量也可由此确定。

2.1.3 水位条件

为了研究过滤装置在可控环境下的效果,研究人员做了7次实验,每次实验均在不同条件下进行(见表1)。如在过滤装置砂砾介质的顶部、底部或中部保持恒定常水位(CWL)(见实验1～3及实验7),或模拟真实暴雨的充水与放空循环,让水位在砂砾过滤装置的顶部和底部之间波动(VWL,见实验4～6)。每次实验都一直运行到过滤装置堵塞为止,当出流量降至初始出流量约10%时,则定义为系统堵塞(尽管有几次实验由于设备故障而过早终止)。

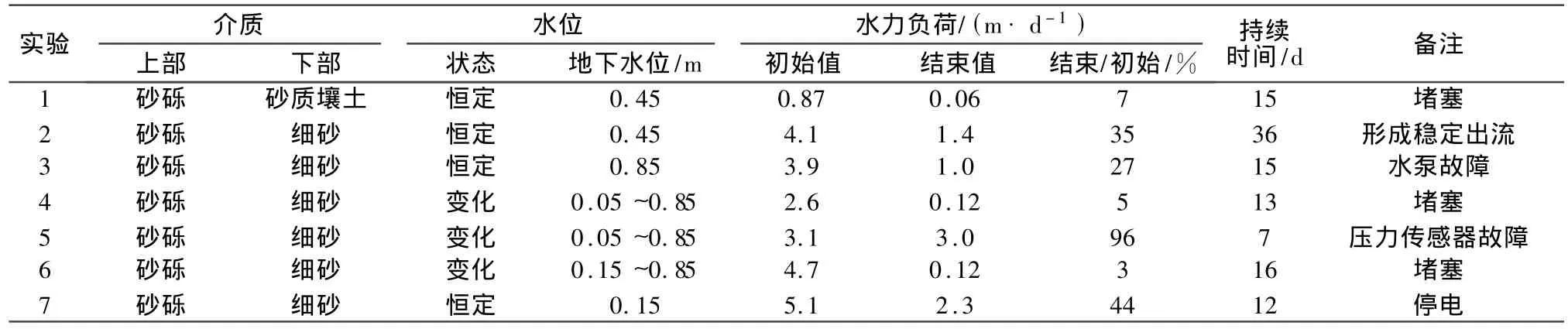
表1 实验的详细记录

2.1.4 水样收集与分析方法

水样在流入口、流出口以及沿砂砾过滤装置深度30、50、70和85 cm处,隔一天取样一次。测量的水质参数为 :TSS、TN、P、可过滤的活性磷(FRP)、铵盐(NH+4)、硝酸及亚硝酸盐(NOx)、溶解性有机氮(DON),以及重金属元素(Cu,Pb和Zn)。这些污染物在城市暴雨径流中较为常见,对水生态系统具有不利影响。2001年,研究人员保罗和梅耶指出,泥沙增加了河道的浊度,是吸附在其表面污染物质(如重金属)的载体,从而提高了雨水中的营养物水平,而这些营养物质则会导致受纳水体的富营养化,且重金属对人类、陆生生物和水生物均有害。

该分析过程根据美国公共卫生协会、美国自来水厂协会和水污染控制联合会出台的质量控制和保证程序标准方法进行,而泥沙粒径分布则采用英国马尔文的MS系列激光衍射粒度分析仪加以测量。

2.2 数据分析

水质样本沿圆柱体(由砂砾石和细砂填充而成,见图1)布置的各取样点被同时取出。但由于存在时滞效应,在某一给定时刻测量得到的出流浓度与流入圆柱体的雨水浓度并无直接关系。因此,雨水进、出过滤装置的时滞问题应采用内插法得以解决。时滞根据采样时刻的流量进行计算:

式中t为延迟时间,L为砂砾过滤装置长度,υ为达西定律中的水流速度,Q为流量,A为过滤装置的横截面积。利用各数据点间的线性插值可计算出相应的出、入流浓度。通过该法,可建立每个取样点污染物浓度的时间序列。

2.2.1 浓度因素分析模型

为了测试过滤系统深度对污染物去除效果的影响,在每次实验中,都需计算每个取样点污染物浓度的算术平均值。科尔莫戈罗夫-斯米尔诺夫检验(p＞0.01)先检验数据分布,得出数据接近正态分布,再用单向方差分析来检验污染物浓度随深度的显著变化(显著性水平在p＜0.05内为可接受)。

利用浓度时间序列,采用多元线性回归,评估流出雨水的污染物浓度与下列可能的解释变量之间的关系。这些解释变量包括:水力负荷、流入雨水的污染物浓度,以及时间(如从实验开始所经历的时间)。对R2值进行分级划分,用以确定每个自变量独立或联合地描述因变量的权重。分级划分法比其他更常用的多变量统计算法(如多元回归法)更有优势,因为该法明确了独立预测变量的相对重要性,即可以对相关性较强的独立变量进行识别,剔除非独立变量因素,由于这些变量与其他独立变量联合相关,因此与非独立变量有着较高的相关性。通过利用独立变量的观测值算出因变量,与从数据矩阵中提取的500个随机生成的因变量集合比较,识别出能够独立解释大部分因变量的自变量。在上限95%的置信区间为显著性可接受(Z统计量≥1 ∶65)。

2.2.2 污染物负荷及其空间分布

利用在取样点测量到的流量和污染物浓度估算每个取样点及流入、流出圆柱体的雨水在整个实验过程的污染物负荷。

式中l为负荷,Qi和Ci为在时刻i时测得的各取样点的流量和浓度,Δ t为2次测量段的时间间隔,N为每次实验的取样总次数。

计算圆柱体内各取样点的污染物负荷以确定污染物沿深度的分布情况。利用测量值将结果加以检验,该测量值是在每次实验结束后测得的积累在圆柱体内的泥沙沉积量。如果泥沙沉积物分布的测量值与计算值相差在10%以内,则可以推论,计算得到的污染物分布数据可以放心使用。

2.2.3 实验结果在等效处理年降雨量中的应用

为了了解实验结果运用于真实砂砾过滤系统在整个寿命期的情况,系统在被堵塞前所处理的雨水量被折算成等量的年降雨量。计算假设集水面积与过滤装置面积比值在0.2%,2%和5%(即砂砾过滤系统的表面尺寸是不透水汇水面积的0.2%,2%和5%)。2005年,阿尔戈和佩扎尼缇指出,这些比值涵盖了实际运用的常见范围。分析采用了墨尔本的典型降雨,多年平均雨量为653 mm/a,该数据是由澳大利亚气象局提供,通过分析1950～1999年(50 a)的6 min降雨量数据得来的。

3 研究结果

3.1 水质浓度的因素分析模型

每次实验均可得出,沿过滤器的平均污染浓度呈现极其相似的形态。

3.1.1 水力负荷

在每次实验里,最大水力负荷都出现在实验第1天,并随着过滤系统逐渐堵塞而稳步下降,最后趋近最低值。然而,水力负荷的降低,使得雨水在过滤系统中的滞留时间也相应增加,这对流出雨水的污染物浓度并无明显的影响,也没有因时间推移而反映这些趋势。

3.1.2 时间因素

尽管一直使用空气循环装置混合雨水,流入雨水的污染物浓度却因雨水配制池内混合情况的变化而变化。然而,即使入流的浓度随时间变化,但出流的TSS却并非如此。在常水位下,出流的重金属离子浓度随时间保持恒定,意味着浓度达到稳定状态,但在水位发生变化的条件下,出流的浓度随时间推移而增加(见实验4～6)。在实验7中,总氮(TN)和硝酸盐/亚硝酸盐氮(NOx)的出流浓度随时间推移而增加,但在其他几个实验里,TN和NOx在很大程度上随入流浓度变化而变化。除实验7外,其他实验中的铵(NH+4)浓度随时间变化而明显增加,通常都超过了入流浓度。

3.1.3 深 度

TSS、TP、TN和重金属离子浓度在过滤装置上部均呈现迅速降低状况。方差分析结果显示,污染物浓度在入口与在深30 cm处有明显不同,但在超过30 cm的各深度间隔之间浓度差别不大,这意味着污染物的去除大多发生在滤层上部的30 cm内。

污染物浓度和滤层深度高度相关性显示,截留与机械筛滤是污染物被去除的主要过程。这与德谢森(Dechesne)等人2002年的发现是一致的,尽管在他们的研究里,过滤装置顶部有一个土壤“盖”,该土壤盖可能会影响到金属离子的吸收情况。

3.1.4 入流浓度、时间及水力负荷的相对重要性

当保持常水位时,水力负荷和入流浓度对泥沙沉积物的去除无影响。然而,分级划分结果显示,时间因素是与出流 TSS相关的显著独立变量。泥沙沉积物的去除量随时间推移而增加,这就意味着出现了泥沙累积(从而减少了泥沙运动和再悬浮状态)和(或)增加了沉淀/粘附在滤料表面的量(由于早先沉积的泥沙颗粒提供的黏性表层为该过程提供了便利)。这与饮用水处理中的砂滤池成熟后(其表层形成滤饼)所观察到的微粒去除效率得以提高相一致。当水位发生变化时,时间并无明显变化,极有可能是因水位变化减小了“栓塞效果”,因此减小了上述“黏性滤料效果”。

美国环保署称,过滤装置能更有效地去除泥沙沉积物,而非TP,原因可能是磷受到其他因素,如温度、氧化还原条件和酸碱度(pH)的影响。在保持常水位时,可识别出所有的预测变量对出流TP浓度有明显影响,但在变化的水位条件下,无明显预测变量。在该例中,入流浓度的显著性可能是由去除率的数学本质造成的,因为出流浓度一定时,去除效率将随着入流浓度的增加而增加。

氮的总体去除率相对比较低,且无预测变量被一致识别出是总氮或某一类型氮的显著独立相关变量。可溶性氮浓度在雨水入口和出口间变化,然而总氮的浓度并无明显变化,证明过滤系统内产生氮循环(氮在不同形式间转化),而非经过反硝化作用或长期生物摄取被有效去除。

时间和水力负荷有明显的相互关联性,因为随着实验时间增长,水力负荷会因堵塞而出现较大幅度地下降。然而,为了说明不由水力负荷控制的时间相关进程,如有机物的衰减,已采用分级划分法以检验各变量的独立影响。

3.2 污染物的空间分布

2007年,锡瑞瓦尔登等人指出,泥沙及其附着污染物的累积取决于水位条件。当保持常水位时,泥沙积聚在水位线附近,形成上述的“栓塞”。当允许水位在过滤装置顶部和底部变化时,泥沙在整个滤层中的分布更为均匀,然而泥沙和重金属元素仍在装置顶部分布较多。同一实验的微粒粒径分布结果显示,较大颗粒分布在过滤装置上部30 cm的范围内,较小微粒则在截留前在滤层中已移动较远距离。但需注意的是,将最低取样点设置在85 cm处,故计算的泥沙累积量并未计入砂砾过滤器底部5 cm的量。研究表明,过滤装置底部也是泥沙累积量较高的位置。

输入的重金属元素中,至少50%被滞留在砂砾层顶部30 cm的范围内,同时,输入的磷和氮,分别有40%和50%滞留在过滤装置上部50 cm的范围内。可溶性营养物质的空间分析显示,随时间推移,磷和氮被截留的状态会被破坏,以溶解形式从滤层中脱离,然而滤层整体效果仍是去除营养物质的“过滤网”。

3.3 污染物处理效率

污染物处理效率是指一次实验中整个砂砾滤层平均污染物负荷的去除百分比,即流入和流出的污染负荷差值除以流入的污染负荷。系统对TSS和TN的处理效率不随水位条件的变化而变化(表2)。但当过滤装置保持常水位时,可观测到TP和重金属的平均负荷削减量比在变化水位条件下的削减量更大,这是因为泥沙沉积主要集中在常水位附近,而TP和重金属则大都附着在泥沙微粒上。在波动水位条件下,较细的微粒与常见附着污染物一同向下移动,至少部分地解释了变化水位条件下截留效率较低的原因。在不同的实验中,流出雨水的溶解性营养物质负荷变化较大,但显然与水位条件或时间因素无关,可能是由于水力负荷和入流浓度均为相对同等重要的解释变量,而没有一直作为显著独立的相关变量引起的(同上所述)。

表2 各水位条件下的处理效率(相同水位条件下测得结果的平均值)

3.4 等量处理的年降雨量

每个过滤装置在被堵塞前(或实验中途终止)所处理的相等体积的年降雨量如表3所示。最大处理水量(实验2,假设集水面积内有5%的渗透面积)相当于6.5 a的降雨,最小处理水量(实验1,假设集水面积内有0.2%的渗透面积)仅为年平均降雨量的1%。这意味着滤层面积与集水面积之比小于5%的砂砾过滤系统作用不大。而在现实中,通常建立相当于5%不透水集水面积的过滤系统是不可能的,尤其是在已建成的城市区域。因此,养护计划应根据渗透系统的尺寸制定(表3)。由此推断,更小的系统建设成本较低,日常运行费用较高,在整个寿命期内总费用可能较低一些。此外,(在较大的渗透系统前使用草坪过滤带、洼地或沉淀池)对雨水进行预处理可能是最实用的选择。

表3 等量处理的年降雨量(在典型的墨尔本气候下)(实验1～7)

3.5 过滤系统设计与运用的意义

虽然实验室规模的圆柱体过滤装置有助于理解砂砾过滤系统中发生变化的过程,但它仍不能完全代表真实环境下的渗透系统。通过实验装置中的雨水量和转移方式与渗透系统在真实环境中遇到的情况不同,如维持水位恒定就没有如实反映真实条件。这些处理方式有助于理解影响水力和水质变化的过程,却不可能通过实地监测到。

当重点考虑去除泥沙沉积物和重金属时,砂砾过滤系统是一种有效的处理措施,但在去除营养物质更为重要时,系统则不那么有效了,尤其是在去除含氮营养物质时。实验结果表明,当过滤器在最不利条件下(通过加大水流注入的速度),污染物的去除效果保持相对稳定,即使滤层介质开始堵塞而增加了水处理的滞留时间及接触时间。

2005年,研究人员发现,砂砾过滤系统在地面以下的最大深度建议值是1.5 m(含0.3 m厚的回填土覆盖层),虽然常见的深度范围为0.3～0.5 m。基于该实验结果,一个深0.5 m的砂砾过滤系统就足以去除泥沙沉积物和重金属元素,而即使系统深度达0.9 m,也不可能得到适度的营养物质去除率,尤其是含氮营养物质。同时,结果还显示,在设计雨水渗透系统时无需对流量进行控制(除非是需要记录雨量,则也需要记录渗透系统的尺寸及能够记录的年平均径流量)。砂砾过滤系统承担的水力负荷很大程度上是由系统周围和底部土壤的水力传导特性(渗透性)决定的,因此砂砾介质的水力负荷变化范围非常有限,这阻碍了砂滤介质中泥沙沉积物的再次运动,但对粒径非常细的泥沙则并非如此。而另一方面,物理堵塞决定了砂砾过滤系统的使用寿命,并非水处理中出现的问题(如污染物质穿透滤层)。因此,有必要对这些系统的运行进行雨水预处理。

2007年,锡瑞瓦尔登等人指出,如果过滤后的雨水径流可以渗入周围土壤,那些没有被滤层去除或被截留后又再次运动的污染物有可能对周围土壤及其地下水造成污染。假如周围土壤粒径的分布与从系统流出的泥沙粒径相匹配,则可推断出没有被截留在砂砾滤料中的微粒将在砂砾滤层的底部累积(即砂砾与土壤的交界面)。假如磷和重金属元素与微粒有很强的亲和力,则很容易被紧邻滤层的土壤所固定。相反,虽然可溶性氮可能会因生物化学反应而转化成移动性较小的形式,但其移动性很强,很容易在土壤中移至较远的地方。

4 结 论

在需去除泥沙沉积物和重金属元素时,砂砾过滤系统是雨水径流的有效处理方式。虽然用于促进生物化学过程的改造系统可能有助于营养物质的去除,但在营养物质是主要污染物的情况下,渗透系统并非合适的选择。就系统深度而言,0.5 m足以去除泥沙沉积物和重金属。砂砾过滤系统的去除效果不受水力负荷和堵塞的影响。假如主要的污染物去除过程是物理过程,且水力负荷率受系统下部土壤的渗透率限制保持在较低水平,则可推断,截留在系统中的泥沙沉积物,伴随着因化学作用被吸附在泥沙表面的污染物,重新流动回到水中的可能性较低。由于细小微粒被缓慢的冲刷通过过滤系统,且(或者)随着滤层的堵塞,酸碱度与含氧量发生改变导致解吸附作用,流出雨水的重金属元素和磷的浓度可能随时间推移而增加。然而,在污染物突破滤层出现之前,物理堵塞会先发生,因此在砂砾过滤系统的整个寿命期内,泥沙沉积物和重金属的去除率会保持较高水平。