二相编码雷达前沿复制干扰的能量效率分析
邱 杰
(海军航空工程学院,山东 烟台 264001)
现代战场环境的发展对雷达的检测能力、分辨力、测量精度以及对反侦察和抗干扰能力等提出了更高的要求。雷达的检测能力在本质上取决于雷达信号的总能量,在发射机输出峰值功率受限的情况下,必须加大雷达信号的时宽以提高雷达信号的总能量,进而提高雷达的检测能力。对于大时宽信号,为了保证雷达的距离分辨力和测量精度,必须通过适当的调制,使其同时具有大的频宽。于是,大时宽带宽积信号被广泛应用于现代雷达。
除检测能力、分辨力、测量精度方面的优势外,大时宽带宽积信号还具有低截获概率方面的反侦察优势,特别是,具有高的能量利用效率方面的抗干扰优势,即在被接收经过匹配滤波器后,可以获得数值为时宽带宽积的峰值功率增益,而传统的噪声干扰的能量利用效率很低,在经过匹配滤波器时基本不能获得增益。
由于雷达信号的时宽带宽积可以很大(几十到几百甚至更大),如果采用传统的噪声干扰,则需要干扰功率增大几十到几百倍甚至更多倍。这对干扰方提出了巨大的挑战。为了与雷达的大时宽带宽积信号和匹配滤波器相抗衡,灵巧噪声干扰的概念[1]被提出并付诸实践,产生了很好的效果。
灵巧噪声干扰的本质含义是:使干扰由多个分量组成,并且使干扰中的每一个分量都获得雷达接收机的匹配滤波增益(通过使干扰中的每一个分量的频谱都与雷达信号的频谱相同来达到此目的),从而使干扰中的每一个分量的能量利用效率都达到最大[2]。
由上述关于灵巧噪声干扰本质含义的表述可知,实施灵巧噪声干扰的关键是及时、准确地获取雷达信号的完整频谱或者波形。
在实际战场环境中,及时、准确地获取雷达信号的完整波形,进而实施灵巧噪声干扰,并不是一件容易的事,而获取雷达信号的部分波形,实施所谓的前沿复制干扰则比较容易。
灵巧噪声干扰和前沿复制干扰的基本出发点都是提高干扰的能量利用效率。这里,能量利用效率是一个基于比较的概念,即对于A、B两种干扰方式,要求产生相同的干扰效果,各种干扰方式需要的干扰信号的能量的比较。如果A方式需要的干扰信号能量低于B方式需要的干扰信号能量,则A方式的能量利用效率高于B方式。如果A方式需要的干扰信号能量为B方式需要的干扰信号能量的1/n,则A方式的能量利用效率为B方式的能量利用效率的n倍。
显然,如果前沿复制干扰可以达到与灵巧噪声干扰相同或者差不多的能量利用效率,就没有必要去实施要花费更大代价的灵巧噪声干扰。因此,有必要对灵巧噪声干扰和前沿复制干扰的能量利用效率进行比较。
二相编码信号是应用非常广泛的一类大时宽带宽积信号,本文针对采用二相编码信号的雷达(以下也简称为二相编码雷达),以实施压制式干扰为目的,对灵巧噪声干扰和前沿复制干扰的能量利用效率进行比较分析。主要内容包括:
1)前沿复制干扰的产生背景;
2)干扰基本成分通过匹配滤波器后的输出信号脉冲峰值分析;
3)能量利用效率比较基准及相关计算公式;
4)典型条件下,灵巧噪声干扰和前沿复制干扰所需能量的数值计算;
5)一般情况下,灵巧噪声干扰和前沿复制干扰的能量利用效率的比较。
1 前沿复制干扰的产生背景
二相编码信号可以表示为
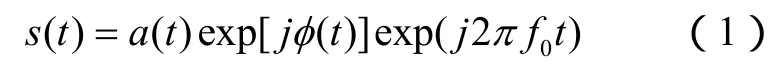
信号的复包络为
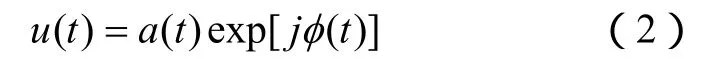
式中,f0为载波信号的频率;a( t)为矩形窗函数;φ( t)为相位调制函数。
φ( t)只有 0、π两个取值,可以用二值相位序列{φk=0,π}表 示 ,ejφ可 以 用 二 值 序 列{ck= e xp( jφk)= 1 ,- 1 }表示。
对于 a ( t)有

式中,τ为码元宽度;p为码长。
如果二相编码信号的f0、ck固定,则利用DRFM技术获取信号波形并实施灵巧噪声干扰是容易的。但如果上述参数发生变化,特别是发生脉间捷变,则仅仅利用DRFM技术将不能有效地实施灵巧噪声干扰。事实上,二相编码雷达中,基于反侦察、抗干扰的目的,ck发生脉间捷变是非常可能的。
在波形脉间捷变的情况下,需要在雷达的每一个脉冲重复周期都获取雷达的当前发射波形,才有可能实施针对性的灵巧噪声干扰。另外,自卫式干扰不可能在距离上覆盖目标回波。要使干扰在距离上覆盖目标回波,干扰机的配置必须在距离上超前于被掩护的目标,但超前距离显然是不能随心所欲的。一种非常实际的情况是,二相编码雷达进行波形脉间捷变,距离上超前部署的干扰机只能获得雷达发射信号的部分波形(通常是前面的部分波形,以下也简称为前沿波形)。将获得的雷达信号的前沿波形进行多次复制,作为基本成分替代雷达信号完整波形[3],再对该基本成分进行噪声卷积调制,形成干扰信号,这就是所谓的前沿复制干扰。
2 匹配滤波器输出信号幅度
[2]以及匹配滤波器的线性特性可知,灵巧噪声干扰和前沿复制干扰的能量利用效率仅取决于基本成分,与调制噪声无关。因此,以下仅针对基本成分进行分析。在分析时,除非必要,不考虑载波。
不失一般性,设{ck}为31位的m序列:
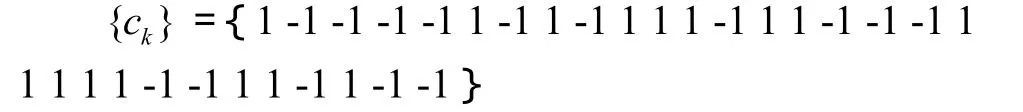
在二相编码雷达中,匹配滤波器可以以时域的相关积累器的形式来实现。对于二相编码信号,相对于频域的FFT处理,相关积累器更为直观。
如图1所示的是对应于上述{ck}的相关积累器的原理性的结构[4]。
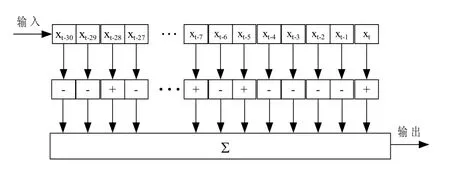
图1 相关积累器原理结构图
图1中,第一行是移位寄存器(或抽头延迟线),其节拍时间为τ。移位寄存器的各位输出分别与对应的取值为±1的加权因子相乘,然后相加。各个加权因子的从右至左的排列顺序与{ck}数位的从左至右的排列顺序相一致。
2.1 灵巧噪声干扰基本成分输出幅度
不计载波信号,二相编码雷达的回波信号(也是灵巧噪声干扰的基本成分)可以表示为[5]
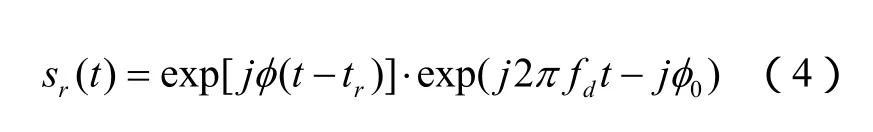
式中:tr为回波延迟时间;fd为回波多普勒频移;0φ为回波信号初始相位。
显然,在回波信号的第一个码元到达相关积累器中移位寄存器的最后一位的时候(记为t0),移位寄存器的各位输出经加权后同相相加,此时相关积累器输出信号(记为 Rs( t0))幅度达到峰值,有
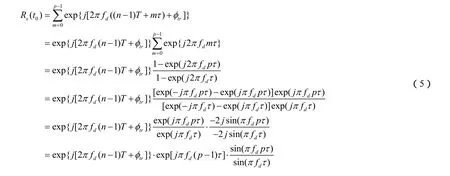
式中,n为脉冲重复周期计数;T为脉冲重复周期;trφ为回波延迟导致的多普勒频移相位。
不计回波信号的多普勒频移,在式(5)中,令fd→ 0 ,得到:

这也是灵巧噪声干扰基本成分通过相关积累器后的输出信号脉冲(宽度为τ)幅度。
2.2 前沿复制干扰基本成分输出幅度
前沿波形可以表示为

对于a/( t),有
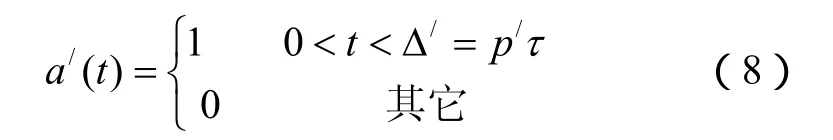
式中, p/为前沿波形码长, p/<p。
不妨假设 p/= 8 ≈p 4。对前沿波形复制三次,得到对二相编码雷达实施前沿复制干扰的基本成分为
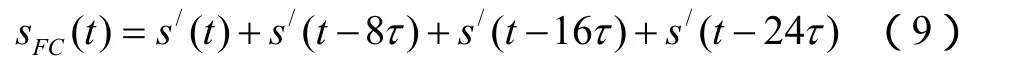
sFC(t)的总长度为4 p/( = 3 2 ≈ p = 3 1)。
s/( t)通过相关积累器后的输出记为U/(t)。
s/( t)的第一个码元到达相关积累器中移位寄存器最后一位的时候(记为),移位寄存器的后8位输出经加权后同相相加,其它各位输出为零。此时相关积累器输出信号(记作())幅度达到峰值,有

令 fd→ 0 ,得到:

这就是s/( t)通过相关积累器后的输出信号脉冲(宽度为τ)幅度。
sFC(t)通过作为线性系统的匹配滤波器后的输出为:
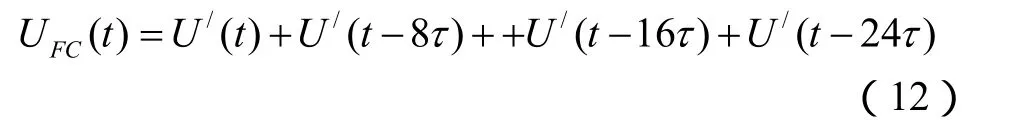
由此可见,在上述情况下,不计距离旁瓣,在相关积累器输出端,得到的是四个幅度为/p、宽度为τ、间隔为的脉冲。
3 能量利用效率比较
3.1 比较基准及相关计算公式
对不同干扰方式能量利用效率的比较必须有一定的基准,这就是要求各种干扰方式对雷达产生相同的干扰效果。在这样的前提下,才可以比较各种干扰方式所需要的干扰信号能量的大小,从而得出各种干扰方式的能量利用效率孰优孰劣的结论。
雷达信号检测通常是一种峰值检测,因此,对于压制式干扰,就基本成分而言,有意义的是其在被干扰雷达的信号检测端产生的干扰脉冲的幅度大小和数量的多少。这里,不妨假设匹配滤波器输出端就是雷达的信号检测端,以在匹配滤波器输出端产生相同数量和相同幅度大小的脉冲为基准,就灵巧噪声干扰和前沿复制干扰的能量利用效率进行比较。
可以认为在匹配滤波器之前,雷达对于灵巧噪声干扰和前沿复制干扰的处理增益是相同的,因此,能量利用效率的比较针对匹配滤波器输入信号进行。
由式(10)、式(11)和式(7)可知,如果实施码长为/
p=8(≈p4)的前沿复制干扰,不计距离旁瓣,前沿复制干扰基本成分通过匹配滤波器后产生的是4个宽度为τ、幅度为/p的脉冲。而如果实施灵巧噪声干扰,要在匹配滤波器输出端产生同样的(指幅度和时间位置相同)4个脉冲,则需要在匹配滤波器输入端输入4个幅度为/p p(≈1/4)的灵巧噪声干扰基本成分。以下给出这两种情况下,各自在匹配滤波器输入端的干扰信号总能量的计算公式。
对于前沿复制干扰,在匹配滤波器输入端的干扰信号总能量的计算公式为
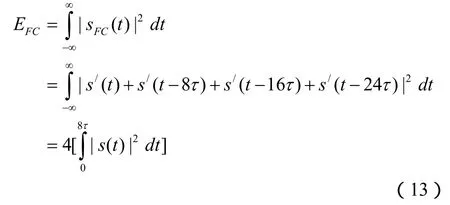
EFC之所以可以写为一个积分式的4倍,是因为sFC(t)中的各段相同而且在时间上互不重叠。
对于灵巧噪声干扰,各个幅度为8 31的灵巧噪声干扰基本成分在时间上是有重叠的,干扰信号总能量的计算公式为
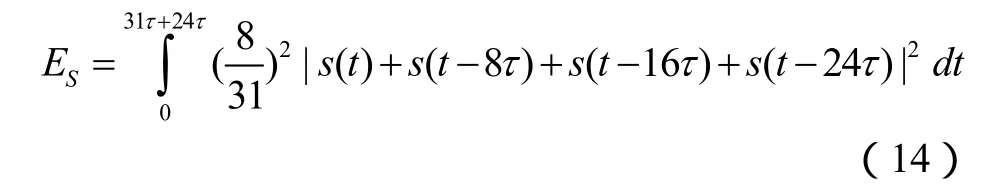
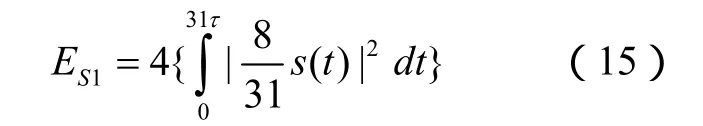
3.2 典型条件下的数值计算
设f0=50MHz,τ=0.2sμ,对式(8)、(9)和(10)进行数值积分计算(事实上,数值积分计算结果与f0和τ的取值没有关系),得到:
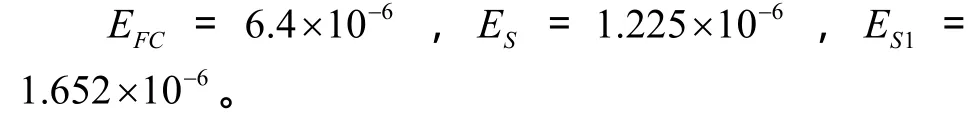
以及:
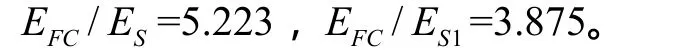
由于是针对信号的复数形式进行计算的,EFC、ES和ES1的数值是实际信号能量数值的两倍,但这并不影响EFC/ES和EFC/ES1的正确性。
上述计算结果表明,在前沿波形宽度为雷达发射信号宽度 8/31(≈1/4)的情况下,如果要求相同的干扰效果,则实施前沿复制干扰所需的能量为实施灵巧噪声干扰所需能量的1/(8/31)(约为4倍)或更多。
进一步,设前沿波形的码长/p分别为6(复制四次,总码长为 6×5=30≈p,相关积累器输出脉冲数为5,幅度为6)、10(复制二次,总码长为10×3=30≈p,相关积累器输出脉冲数为3,幅度为10)、16(复制一次,总码长为16×2=32≈p,相关积累器输出脉冲数为2,幅度为16),实施前沿复制干扰。作为对比,在匹配滤波器输入端,分别输入五个幅度为6/31的灵巧噪声干扰基本成分(与前沿波形码长/p=6对应)、三个幅度为10/31的灵巧噪声干扰基本成分(与前沿波形码长对应)、二个幅度为16/31的灵巧噪声干扰基本成分(与前沿波形码长/p=16对应),实施灵巧噪声干扰。这四组情况下(包括/p=8),实施前沿复制干扰和实施灵巧噪声干扰,产生的干扰效果是相同的。
以下给出这四组情况下,前沿复制干扰和灵巧噪声干扰各自在匹配滤波器输入端的干扰信号总能量的比。

表1 数据按EFC/ES、EFC/ES1的顺序排列表
表1中数据说明:
1)在前沿波形宽度为雷达发射信号宽度/p p的情况下,如果要求相同的干扰效果,则实施前沿复制干扰所需的能量为实施灵巧噪声干扰所需能量的或更多
2)在相同条件下,ES<ES1。
对于上述的1),还可以更为直观地进行如下的解读:
p/=6时, p// p ≈ 1 /5,实施前沿复制干扰所需的能量约为实施灵巧噪声干扰所需能量的 5倍(EFC/ES1)或更多(EFC/ES);
p/=8时, p// p ≈ 1 /4,实施前沿复制干扰所需的能量约为实施灵巧噪声干扰所需能量的 4倍(EFC/ES1)或更多(EFC/ES);
p/=10时, p// p ≈ 1 /3,实施前沿复制干扰所需的能量约为实施灵巧噪声干扰所需能量的 3倍(EFC/ES1)或更多(EFC/ES);
p/=16时, p// p ≈ 1 /2,实施前沿复制干扰所需的能量约为实施灵巧噪声干扰所需能量的 2倍(EFC/ES1)或更多(EFC/ES)。
3.3 一般情况下的比较和结论
为适应一般情况下的分析和简化讨论起见,将各种信号用正弦信号的形式来近似,则各种信号的能量可以统一表示为

式中:x为信号标识; fac为固定因子;A为信号幅度;T为信号持续时间。
对(7)式进行推广:设/p=p/n,对前沿波形复制(n-1)次,得到对二相编码雷达实施前沿复制干扰的基本成分为:

对应的干扰信号总能量为
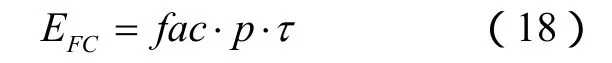
按照前面提出的能量利用效率比较基准,对应于p/=p/n,前沿波形复制(n-1)次产生的前沿复制干扰,对于灵巧噪声干扰,需要 n个幅度为/p p=1/n的灵巧噪声干扰基本成分。考虑各个幅度为1/n的灵巧噪声干扰基本成分不重叠的情况,灵巧噪声干扰的干扰信号总能量可以写成:
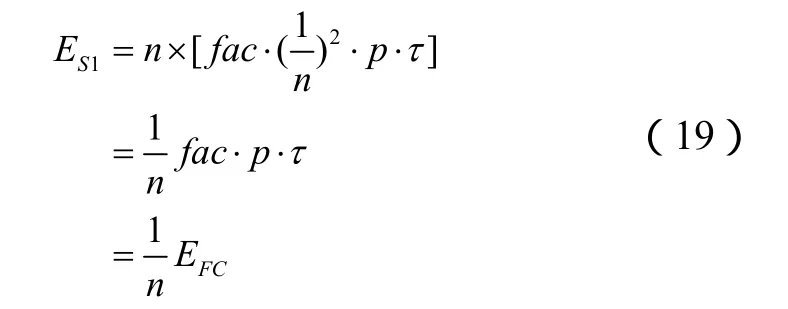
由式(13)可知,在前沿波形宽度为雷达发射信号宽度1/n的情况下,如果要求相同的干扰效果,则实施前沿复制干扰所需的能量为实施灵巧噪声干扰所需能量的n倍,前沿复制干扰的能量利用效率仅为灵巧噪声干扰的能量利用效率的1/n。考虑到ES<ES1的事实,上述结论得到进一步的加强。
4 结束语
前沿复制干扰的实施较为容易,但其干扰信号能量利用效率相对于灵巧噪声干扰的干扰信号能量利用效率有明显下降。前沿波形的时间宽度越短,其干扰信号能量利用效率下降得越厉害,这使得干扰方难以承受。
提高干扰信号能量利用效率的有效途径是实施真正意义上的灵巧噪声干扰,前提是准确地超前获取雷达的当前发射信号波形。对于进行编码捷变的二相编码雷达,准确地超前获取雷达的当前发射信号波形,并及时地实施针对性的灵巧噪声干扰,尚有一些问题需要解决。
参考文献:
[1]Schleher DC.Electronic warfare in the information age[M].Artech House,1999.
[2]邱杰. 灵巧噪声干扰本质含义探讨[J]. 海军航空工程学院学报, 2011, 26(5).
[3]陈秋东. 灵巧噪声干扰的仿真研究[D]. 南京:南京理工大学,2007.
[4]林茂庸,柯有安. 雷达信号理论[M]. 北京:国防工业出版社,1981.
[5]卢护林. 二相编码信号旁瓣抑制及多普勒补偿算法研究[D]. 西安:西安电子科技大学,2009.

