“粒子源”问题归类与解析

肖照明

（宜昌市夷陵中学 湖北 宜昌 443000）

2010年高考全国理综能力测试卷Ⅰ，Ⅱ物理压卷题，虽然仍是粒子在磁场中的偏转，但不是单个带电粒子在磁场中的多阶段运动，而是由“粒子源”从同一点发出多个同速率不同方向的同种粒子在磁场中的运动问题.有关“粒子源”问题.笔者认为可以从以下几方面归纳解析.

1 探究粒子所经过的区域

【例1】（2005年高考全国卷）如图1，在一水平放置的平板MN的上方有匀强磁场，磁感应强度的大小为B，磁场方向垂直于纸面向里，平板中心有一小孔.许多质量为m电荷为＋q的粒子，以相同的速率，沿位于纸面内的各个方向，由小孔口射入磁场区域.不计重力，不计粒子间的相互影响.图2中阴影部分表示带电粒子可能经过的区域，其中哪个图是正确的？

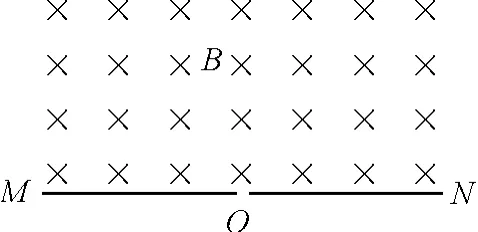
图1

图2

解析：由于所有粒子的质量、电荷量及速度大小均相同，且都从O点开始做圆周运动，因此所有粒子做圆周运动的圆心在以O点为圆心、的圆周O1上.由于圆上最远两点的距离为直径，所以粒子只能在以O点为圆心、的圆O2内运动（图3）.再找粒子的边界速度v1对应的圆O3.改变粒子的入射方向，即使圆O3的圆心在圆O1上移动观察粒子在MN上方经过的区域（图3虚线圆弧）.答案选项A就很容易选出.

拓展：如果粒子的入射方向改为“沿位于平面内与ON成0°～90°角的范围内，由小孔口射入磁场区域”，结果又如何呢？

解析：我们还是要如例题一样做出圆O1，O2，O3.在移动圆O3时就只能在90°范围内移动.仔细观察粒子能经过的区域应该是图4的阴影部分.这里有一个桃叶形状的区域A是没有粒子到达的.这点很容易忽略.

当然，确定了粒子所能经过的区域形状，求其面积就简单了.

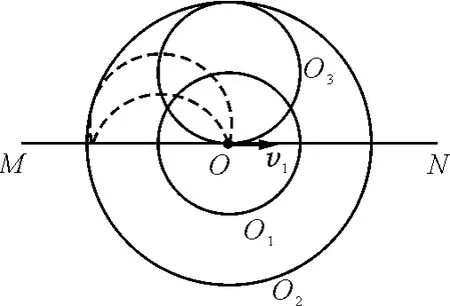
图3

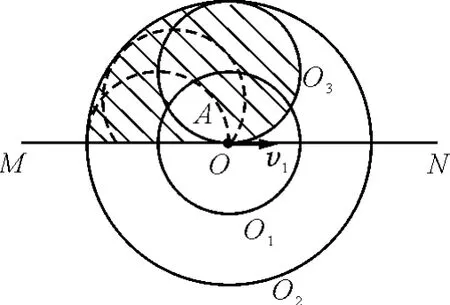
图4

2 探究粒子能打中板的范围

【例2】（2004年高考广东卷）如图5，真空室内存在匀强磁场，磁场方向垂直于纸面向里，磁感应强度的大小B＝0.60T，磁场内有一块平面感光板ab，板面与磁场方向平行，在距ab的距离l＝16cm处，有一个点状的α放射源S，它向各个方向发射α粒子，α粒子的速度都是v＝3.0×106m／s.已知α粒子的电荷与质量之比现只考虑在图纸平面中运动的α粒子.求ab上被α粒子打中的区域的长度.

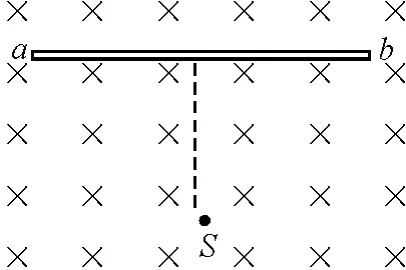
图5

解析：α粒子带正电，故在磁场中沿逆时针方向做匀速圆周运动，用R表示轨道半径，有

由此得

代入数值得

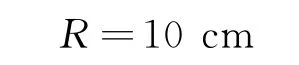
可见

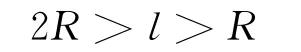
因朝不同方向发射的α粒子的圆轨迹都过S，因此所有粒子做圆周运动的圆心在以S点为圆心、半径为R的圆周O1上.由于圆上最远两点的距离为直径，所以粒子只能在S点为圆心、半径为2R的圆O2内运动.圆O2与ab交于M，Q两点.利用左手定则以SM为直径，粒子可到达M.但不能到达Q点.由图6中几何关系得

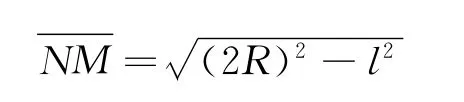
粒子的轨迹圆的圆心在O1上运动，通过作图（图6）可知：圆轨迹在图中N左侧与ab相切的切点P就是α粒子能打中的左侧最远点.如图作辅助线可求出

故所求长度为

代入数值得

图6

3 探究粒子通过磁场的时间

（1）粒子在磁场中做圆周运动的半径R及粒子的比荷

（2）此时刻仍在磁场中的粒子的初速度方向与y轴正方向夹角的取值范围；

（3）从粒子发射到全部粒子离开磁场所用的时间.

图7

图8

解析：（1）粒子沿y轴的正方向进入磁场，从P点经过，做的垂直平分线与x轴的交点为圆心（图8），根据直角三角形有

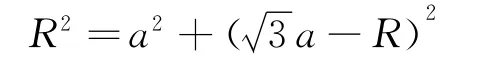
解得

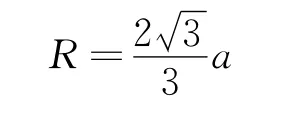
及

则粒子做圆周运动的的圆心角为120°，周期为T＝3t0.粒子做圆周运动的向心力由洛伦兹力提供，根据牛顿第二定律得

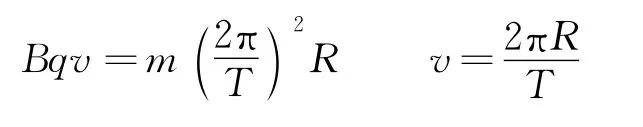
化简得

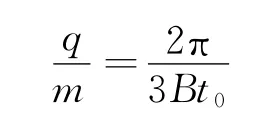
（2）因为是同号粒子以同样的速度从O点同时出发，进入相同的磁场，所以此时还在磁场中的粒子运动轨迹都是圆心角为120°的圆弧.且此圆弧的圆心都在以O为圆心、半径为的圆周上.如图9所示，还在磁场中的粒子其初速度方向与y轴正方向的夹角在v1，v2与y轴正方向的夹角之间.由几何关系很容易得到v1与y轴正方向的夹角为60°，v2与y轴正方向的夹角为120°.所以初速度与y轴的正方向的夹角范围是60°到120°的粒子仍在磁场中.

图9

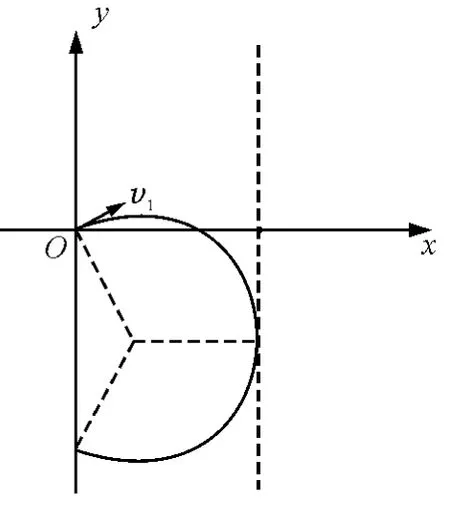
图10

（3）在磁场中运动时间最长的粒子的轨迹应该与磁场的右边界相切（图10）.在三角形中两个相等的腰为而它的高是

半径与y轴的的夹角是30°，这种粒子的圆心角是240°.

所以从粒子发射到全部离开所用时间为2t0.

4 探究粒子运动的条件

【例4】如图11，从粒子源O以相同速率v0在xOy平面内朝x轴上方的各个方向射出质量均为m、电荷均为q的带负电的一簇粒子（即0＜θ≤π），不计重力及粒子间的相互作用.试在图中的适当区域加一垂直于xOy平面、磁感应强度为B的匀强磁场，使这簇带电粒子通过该磁场后都沿平行于x轴方向运动.在图中定性画出所加的最小磁场区域边界的形状和位置.

解析：分析沿x轴成θ角射出的粒子，其在磁场中的半径为粒子在A点射出磁场.设A点的坐标为（x，y）.如图12，利用勾股定理得

图11

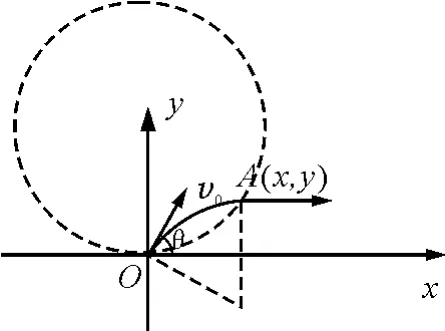
图12

即满足题意的磁场边界为以O为圆心、R为半径的圆.

同理，平行射出的“粒子束”也可以经此类磁场偏转后汇聚于某一点，便于收集.这也在近几年的高考题中经常出现.

虽然粒子源问题对学生的综合能力的要求比较高，但只要掌握好其基本规律，用好基本方法，突破它是容易的.