航空发动机结构可靠性优化方法研究

胡殿印，王荣桥，陈景阳，樊 江

(北京航空航天大学 能源与动力工程学院，北京100191)

1 引言

随着航空燃气涡轮发动机对高效率和高推重比的不断追求，其主要构件——尤其是热端件承受着越来越高的温度和循环载荷的作用，因此就要要求这些构件除具有足够的强度、刚度和使用寿命外，还要有高的安全性和可靠性。为了解决性能和可靠性这对矛盾，开展航空发动机结构可靠性设计方法研究尤为重要。

在航空发动机传统设计中，通常采用确定性的模型和参数，对设计过程中需要考虑的载荷、材料、几何尺寸、边界条件等简化假设为确定性。并且采用传统的安全因子方法考虑不确定性，常常造成结构重量增加、材料浪费。而基于可靠性的优化设计在设计过程中充分考虑各种随机因素的影响，把结构可靠性作为设计目标或约束，保证获得的设计是在一定可靠度意义下的最优设计[1，2]。

不过传统的基于梯度的优化算法在进行可靠性优化设计时，需要考虑目标函数和约束条件对设计变量的导数，常常存在函数求导困难或不能求导的情况，使得可靠性优化设计无法开展；同时，传统优化算法还往往受限于初始值的大小，会收敛于局部最小解。而智能优化算法的出现，有效避免了传统优化算法所遇到的求导问题，迅速地得到广泛推广与应用。据此，本文提出了采用多项式响应面的近似模型和模拟退火寻优技术的航空发动机结构可靠性优化方法。

2 可靠性优化方法

航空发动机结构可靠性优化分析，将可靠度作为状态变量加入约束中，每进行一次迭代就要进行一次结构可靠性求解，其时间复杂度无法承受。为解决上述问题，在优化过程中引入近似技术，在不降低求解精度的情况下，构造一个计算量小、计算结果与实际仿真结果相近的数学模型来代替实际仿真程序，并在迭代中不断更新，在保证计算精度的前提下使可靠性优化分析效率更高。

本文提出的航空发动机结构可靠性优化方法，其流程如图1所示。通过近似模型[3]将目标函数和状态变量形成响应面模型，利用模拟退火算法[4]对响应面模型进行优化，获取响应面模型最优点；利用响应面模型最优点进行精确有限元计算，校核约束及其目标函数；如果不满足条件，则利用新的计算点代替响应面模型中的目标最大点，重新构造响应面模型，然后再采用模拟退火算法(流程见图2)进行优化，直至满足条件，获取全局最优点。

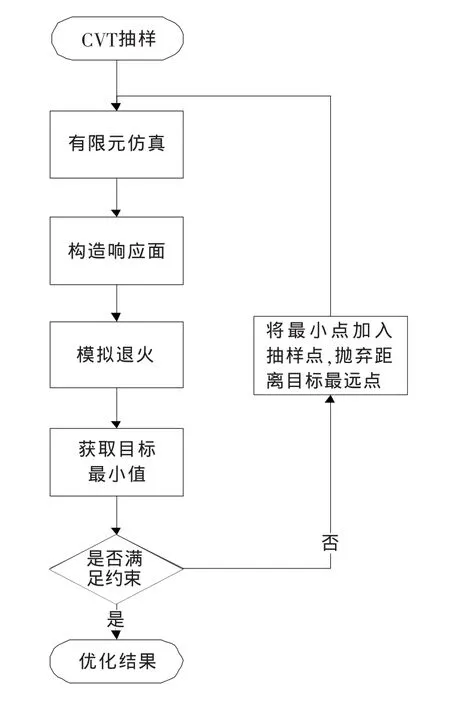
图1 航空发动机结构可靠性优化流程Fig.1 Flowchart of reliability-based optimization design for aero-engine structure

图2 模拟退火算法流程Fig.2 Flowchart of simulated annealing algorithm

下面以某型涡轮盘结构的二维优化分析为例，通过对比多种优化方法来验证本文所提算法的可行性。设计变量的取值范围必须保证优化过程中几何实体的拓扑关系不变。依据涡轮盘强度设计准则[5]确定的状态变量如表1所示。重量作为涡轮盘形状优化的目标函数，即在满足强度约束的条件下重量达到最轻。

表1 状态变量Table 1 The state variables

本文选择4种优化方法对上述优化问题进行仿真来比较算法的可行性：方法1为响应面+模拟退火，方法2为iSIGHT平台最速下降法，方法3为iSIGHT平台序列二次规划，方法4为iSIGHT平台最速下降法与序列二次规划混合优化。从表2中的优化结果可以看出：

表2 优化方法比较Table 2 The comparisons of optimization methods

(1)在结果精度上，方法1与方法3和方法4的仿真结果接近，比方法2的求解结果好。

(2)在计算效率上，方法3和方法4采用的序列二次规划迭代次数多，每迭代一次都要进行一次有限元仿真，计算时间长；方法1的迭代次数最少，计算效率最高。

3 涡轮盘结构可靠性优化分析

以某型发动机高压涡轮盘为对象，在课题组自行开发的可靠性分析优化平台[6]上(见图3)完成涡轮盘结构可靠性优化分析。

轮盘子午面示意图如图4所示。对涡轮盘低循环疲劳寿命和疲劳-蠕变耦合寿命分别进行可靠性分析，两种失效模式所采用的寿命模型见文献[6]，随机变量见表3。温度载荷选用线性分布，轮缘581℃，轮心360℃；轮盘外载为叶片等效离心力和去掉的榫槽部分的等效离心力，参考文献[7]将叶片及去掉的榫槽部分产生的离心力转换为压强施加于轮缘处。可靠性优化分析的变量见表4。表中，变量区间的设定以不改变涡轮盘截面拓扑形状为条件，强度约束参考涡轮盘强度设计准则。

可靠性优化中采用不交叉响应面模拟状态变量与设计变量的关系，采用交叉响应面模拟可靠性寿命与随机变量的关系。模拟退火算法的参数选取为：Markov链长400，初始温度100，衰减系数0.8，结束准则s=6，接受准则初始值0.05。

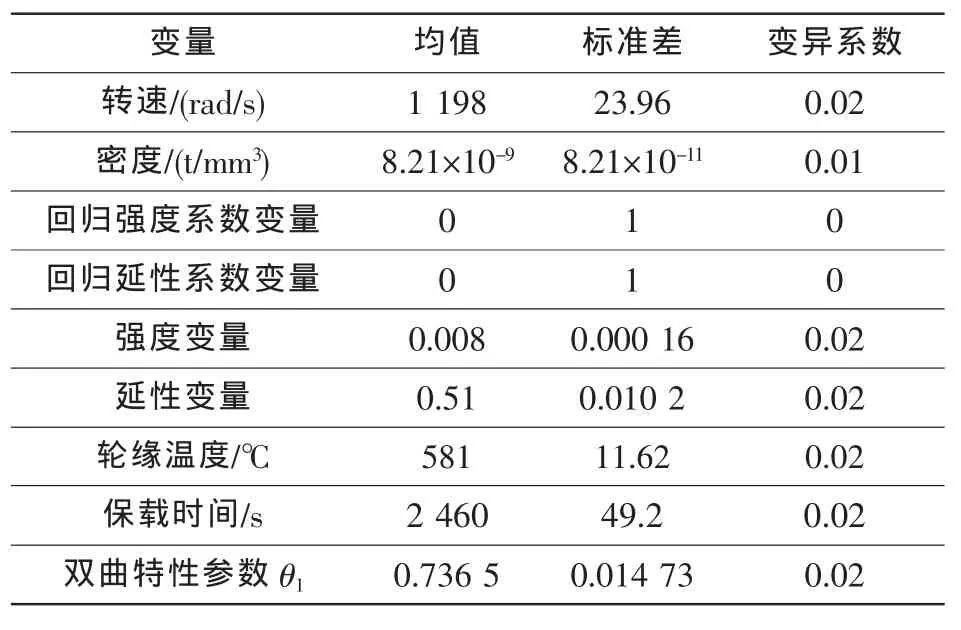
表3 随机变量Table 3 The random variables

表4 涡轮盘优化变量Table 4 The optimization variables of turbine disk

经过优化分析后的涡轮盘在满足强度约束和可靠性寿命约束的前提下重量为41.92 kg，减轻了4.62%。优化后模型的等效应力和等效应变分别见图5、图6，各变量优化前后对比见表5。优化后的涡轮盘结构低循环疲劳寿命和疲劳-蠕变耦合寿命分布直方图分别见图7、图8。

表5 优化变量对比Table 5 Comparisons of optimization variables

从优化结果可以看出，涡轮盘在减重4.62%的情况下，低循环疲劳寿命有所提高，而疲劳-蠕变耦合寿命有所降低。这主要是因为在优化过程中，涡轮盘最大等效应力有所降低，使得低循环疲劳峰值应力降低，所以寿命提高；而疲劳-蠕变耦合考查点在高温的腹板部位，从平均周向应力和平均径向应力可以看出，这部分应力有所提高，故疲劳-蠕变耦合寿命降低，但都满足可靠度指标。

4 结论

本文将响应面模型和模拟退火算法引入航空发动机结构可靠性优化分析中，提出了采用多项式响应面为近似模型构造状态变量和目标函数与设计变量的关系，利用模拟退火算法对响应面模型进行寻优，通过替代距离目标最远点，重构响应面进行模拟退火的寻优方法。涡轮盘的优化分析结果表明，本文提出的可靠性优化方法合理可行，在满足计算精度情况下计算效率得到提高。

最后，在课题组自行开发的可靠性分析优化平台上实现了涡轮盘结构的可靠性优化设计，将低循环疲劳寿命和疲劳-蠕变耦合寿命作为可靠性约束指标。结果表明，涡轮盘在满足强度和可靠性要求的前提下重量减轻了4.62%。该平台不仅适用于涡轮盘，也适用于其他结构的可靠性分析与优化，具有一定的工程意义。

致谢：感谢“凡舟”青年基金(20110401)和中国博士后科学基金(20090460189)提供的资助。

[1]倪 俊，虞跨海，岳珠峰.基于可靠性的涡轮叶片双循环多学科设计优化 [J].航空动力学报，2009，24(9)：2051—2056.

[2]郭书祥，吕振宙，李为吉，等.论基于概率模型的结构可靠性优化设计[J].空军工程大学学报，2001，2(2)：67—70.

[3]韩永志.涡轮叶片多学科设计优化及近似技术研究[D].西安：西北工业大学，2007.

[4]康立山，谢 云，尤矢勇.非数值并行算法(第一册)—模拟退火算法[M].北京：科学出版社，2003.

[5]吕文林.航空涡喷、涡扇发动机结构设计准则[M].北京：中国航空工业总公司发动机系统工程局，1997.

[6]陈景阳.基于可靠性的涡轮盘优化方法研究[D].北京：北京航空航天大学，2010.

[7]鲁华平.涡轮盘低周疲劳寿命可靠性分析及试验评估[D].西安：西北工业大学，2005.