基于移动最小二乘法表面的曲率计算及应用

唐民丽，王 伟

（海南软件职业技术学院 海南 琼海 571400）

三维信息获取技术的高速发展使得我们能方便地获得物体表面三维点云数据。点云数据在三维建模和可视化，以及反求工程中的应用日益广泛。这使得点云数据的几何元素提取和分析受到越来越多的重视。其中，三维点云模型表面曲率估算是点云数据应用的关键技术之一。

点云曲率估算的方法，国内外已经有了一定的研究[1-4]。在三角网格模型上进行曲率估算。这些用其他模型代替原三维点云模型方法的不足在于：1）建立起来的模型表面粗糙，含有很多的噪声点；2）不能保证点与点之间的拓扑关系；3）模型建立过程太复杂。

Levin[5]提出了移动最小二乘法（MLS）构建原始三维表面的投影表面，该方法及相应改进的该方法已经成功地应用在三维建模和绘制中[6]。

文中通过给出具体的移动最小二乘法表面的建立过程，并尝试直接在MLS表面计算点云曲率，将该方法应用在一段隧道扫描三维点云数据的压缩中。

Amenta 和 Kil[8-9]用一个内积函数 e（y，a）沿向量场 n（x）方向的局部最小值具体的定义了MLS表面这里y为一个位置向量，a为一个方向向量。根据该方法，MLS表面建立的两个关键步骤为向量场n（x）的确定以及搜寻内积函数e（y，n（x））的最小极值点。

步骤一：n（x）的确定

假定输入点云为 Q，qi∈Q且 R3，vi为 qi对应的法向量，则向量场n（x）可以由下式给出：

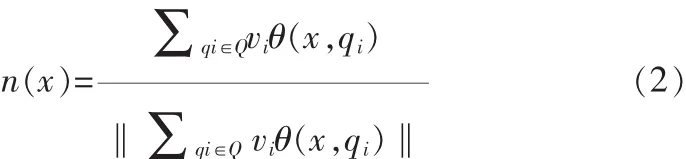
1 MLS表面的建立

如果输入数据没有给出vi，可以通过qi与临近的点来估计qi对应的法向量vi。具体方法如下：

对于给定的采样点q，假定与q临近的采样点的集合为Q，且qi∈Q，则点q的临近点的加权质心c为：

Levin最早提出了MLS表面S的定义[7]：它是原三维模型表面的一个映射。假设映射函数为ψp，则S定义如下：

这里，θ（x，qi）=e-‖q-qi‖2/h2为高斯加权函数，h 为高斯尺度参数，它决定了高斯内核的宽度。文献[10]给出了h的详细说明和选取准则。在文中，选取h为一个常数，这已经能够满足大多数应用的需要。点q的3×3相关矩阵由下式给出：

这里，C为对称阵和正半定矩阵，它的3个特征值λ0，λ1，λ2为实数。 假设 λ0＜λ1＜λ2，用 λ0的特征向量 v0的单位法向量来估计点q的法向量v。

步骤二：MLS表面的投影过程

为了计算MLS表面的曲率，首先我们考虑用一个隐函数来表示MLS曲面。根据文献[4-6]，该隐函数可以表示如下：

对e（y，n（x））函数的局部最小值的搜索等价于对函数求偏导数，并寻找其最小极值点。则MLS表面可以由下式确定：

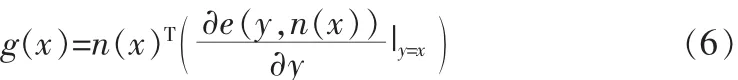
这里 x∈R3，n（x）由（2）式确定，e（s，n（x））由（5）式确定。

2 曲率计算

根据文献[11]，由（6）式得到的MLS表面表达式，高斯曲率和平均曲率计算公式如下：

3 实 验

为了验证算法的正确性，文中采用标准的合成数据做了验证。实验中=0.025，实验数据中每点的法向量为已知的，实验结果如下表：

表1 主曲率和在标准曲面上计算误差分析Tab.1 Results of k1and k2errors on synthetic data

3 个标准几何体的点云数据分别来至于各自对应的实际物体的表面等距采样，采样点为5 000个，如图1所示。

4 数据压缩

以文中曲率算法为基础，提出了一种海量的点云数据压缩的方法，在大于给定阈值的地方保留该点，在小于给定阈值的地方，删除相应点。

图1 3个几何体的三维点云原始模型Fig.1 Nominal geometry for three primitive surfaces

运用文中的数据简化方案对三维隧道扫描点云数据进行了压缩，点云个数为38 645。图2（b）是简化后的数据点，可见用较少的点也能很好的反映物体特征信息。由于本简化方案是基于散乱点集表示的曲面曲率，曲率计算与临近点的个数和的值密切相关。实践中，k取10，h取0.06，效果比较好。

5 结束语

基于MLS表面直接求点云曲率更方便，具有广阔的应用前景，不足之处在于，曲率计算精度和临近采样点个数k和高斯内核宽度h有密切关系，后续的工作中是找到更好的定义k与h的方法，提高曲率计算精度和计算速度。

图2 三维隧道点云模型数据压缩Fig.2 The data compression for 3-d point-cloud model of the tunnel

[1]Amenta N，Bern M，Kamvysselis M.A new voronoi-based surface Reconstruction Algorithm [C]//Proc.SIGGRAPH，1998：415-422.

[2]Bajaj C L，Bernardini F，XU G.Automatic reconstruction of surfacesand scalarfields from 3D Scans.[C]//Proc.SIGGRAPH，1995：109-118.

[3]Bernardini F， Mittleman J， Rushmeier H，et al.The ballpivoting algorithm for surface reconstruction [J].IEEE Transactions Visualization and Computer Graphics，1999，5（4）：349-359.

[4]Boissonnat J D.Geometric structues for three-dimensional shape representation[J].ACM Trans.Graphics，1984，3（4）：266-286.

[5]Levin D.Mesh-independent surfaceinterpolation[J].Geometric Modelling for Scientific Visualization，2003，Springer-Verlag：37-49.

[6]Dey T K，Sun J.An Adaptive MLS surfaces for reconstruction with guarantees[C]//Proc.Eurographics Symposium on Geometry Processing.2005，http：//www.cse.ohio-state.edul%7.Etamaldey/omls.html.

[7]Levin D.The approximation power of moving least-squares[J].Mathematics of Computation.1998，67（224）：1517-1531.

[8]Amenta N，Kil Y J.Defining point-set surfaces[J].ACM Trans.Graph， 2004， 23（3）：264-270.

[9]Amenta N，Kil Y J.The domain of appoint set surface[J].Eurographics Symposium Workshop on Point-Based Graphics，2004：139-147.

[10]Pauly M.Point primitives for interactive modeling and processingof 3d geometry[D].Ph.D.Thesis.Zurich：ETH Zurich，2003.

[11]Goldman R.Curvature formulas for implicit curves and surfaces[J].Computer Aided Geometric Design，2005，22（7）：632-658.