求选编钩计划最优下落方案的一种最短路算法

孙 焰，牟世斌，张俊杰，张方华

（同济大学 交通运输工程学院，上海 201804）

调车作业是铁路运输生产过程的重要组成部分，也是行车组织的一项重要而复杂的工作。调车作业计划编制的要求是尽量提高调车作业效率，减少调车作业时间。而调车作业效率主要是由作业中发生的连挂钩数、溜放钩数和带动的车辆数等因素决定的。机车进入股道将车辆牵出称为一个连挂钩；用溜放的方法分解车列时，每分解一组称为一个溜放钩。由于在技术站连挂钩的效率一般远低于溜放钩，因此有关选编钩计划优化编制的研究目标大多是使连挂钩数最少。传统的下落列及合并方法可保证总连挂钩数最少，但由于车列的下落方案不惟一，而且不同的下落方案直接影响溜放钩的数目。本文的研究主要是从大量的下落方案中寻找最优方案的定量模型及有效算法 (最优方案为最优调车后车组的排列顺序在对应线路不受限时的下落方案）。

1 传统车组下落方法存在的问题

在编制调车作业计划时，首先要进行的是“车组下落”，即为了调整车组顺序，把待编车列中的反顺序车组分解到不同线路上[1]。而后根据车组下落的情况进行“合并下落列”等作业来得到调车方案，不同的车组下落方案对应着不同的调车方案。因此，车组下落情况对调车方案的优劣有重要影响。

例如，待编车列中车组排列顺序为 1 2 1 3 4 2 3，要求按站顺选编。采用传统方法下落后的车组情况如图1所示。则用3条线的选编钩计划为(待编车列停留在①线)：1＋6，2－1，1－1，2－1，3－1，1－1，2－1，3＋1，2＋3，1－4，共用了 3 个连挂钩和7个溜放钩。但若按图2所示方案分组，则同样使用3条线的选编钩计划为(待编车列停留在②线)：2＋5，1－1，3－2，2－2，3＋2，2＋4，1－6，共用了3个连挂钩和4个溜放钩。

图1 传统方法的车组下落情况

图2 较优方案的车组下落情况

由此可见，在其他条件不变的情况下，仅改变车组的下落方案，就可使调车作业量发生明显变化。不同车组下落方案对选编钩计划的优劣有着决定性影响，主要是因为存在“可调车组”，即下落位置可以在相邻列之间调整而仍然符合连接正顺序的车组。而可调车组又分为必可调车组和传递可调车组。根据传递可调车组对其他可调车组的依赖程度，可以分为一次传递可调车组、二次传递可调车组……[2]。

虽然有学者对有关问题进行了研究，如使用“分析计算法[3]”计算各方案下车组的合列系数，并给出了一些判别条件和调整方法[2，4]。但是，由于各车组下落的组合情况太多，仍无完善的定量判别准则和方法。有关研究都是基于统筹对口调车法，在保证连挂钩最少条件下对溜放钩进行优化，并寻找各车组的有利下落位置，但是其“筛选—优化—计算”仍不能完全由计算机来实现[1-4]；也有研究提出了“消逆法”保证了“牵推钩”最少，并能够发挥“箭翎线”的技术优势，但是其“真逆组号”的判定与传统下落列的方法是相似的，并未有明显改进[5]；有的研究运用了基数排序的思想进行调车，但是其优化的方法尚不完善[6]。

可调车组下落位置的不同其实质是同一到站的车组在其最终按站顺选编完成后的车列中的排列顺序不同。因此，只要求得待编车列调车后各车组的最优排列顺序，其对应的下落方案就是最优下落方案。本研究将调车后车组的最优排列顺序的求解转化为图论模型来进行求解。

2 求最优车组排列顺序的一种图论模型

求按站顺调车后的车组最优排列顺序可以转化为求一个有向图的最小 Hamilton 路问题。一个图或有向图中的 Hamilton 路 (回路) 是通过图中每个顶点一次且恰好一次的路 (回路)。

2.1 根据车列特性将问题转化为有向图模型

观察站顺后的车列可以发现，从首组到尾组，各车组是一个有序的排列。除首组和尾组外，每个车组都有一个与其相邻的前序和后继车组。在待编车列中，若按照调车后的站顺，用有向弧依次将其相连，则从首组到尾组是一条 Hamilton 路，各种不同可行的调车后的排列顺序对应着不同的 Hamilton路，其中最小的 Hamilton 路则对应着调车后车组的最优排列顺序。由于首站和尾站可能含有多个车组，均可相应作为首组和尾组，因此需要增加两个虚拟车组：一个虚拟起点车组与首组有向相连；一个虚拟终点车组与尾组有向相连。则调车后的车列在原待编车列中对应着一个从虚拟起点到虚拟终点的有向路径，而这个路径经过每个车组一次且恰好一次，即一个 Hamilton 路。

设有一列由 n 个车组 m 个到达站组成的车列，其原始排列顺序为 i1,i2,…,in，其中ij是{1,2,…,m}中的一个元素，表示其到达站的序号，j 表示车组在车列中的位置，如上例中 i1＝1，i2＝2，i3＝1，i4＝3……。按以下方法转化为一个 n＋2 个点的有向图 G (V,E )。

（1）点集 V＝{0,i1,i2,…，in，m＋1}，将每个车组设为一个点，并虚增两个点 i0和 in+1，且 i0＝0，in+1＝m＋1。

（2）弧集 E＝{ejk| 节点 ij到节点 ik有有向弧相连，当且仅当 ij＝ik或 ij＝ik－1}；即某个车组只与相同车站或紧后车站的车组有弧相连。

（3）弧长C＝{cjk}，若节点 ij到节点 ik有弧相连，则弧上的权为：

弧长为二维向量，第一个分量为连挂钩权，第二个分量为溜放钩权。j＝k－1 表示正向弧 (调车前后车组相对顺序不变)且相邻，调车时两车组不再拆分，可作为一个车组看待，因此弧长为 (0,0)；j＜k－1 表示正向弧但不相邻，需多增加一个溜放钩使其相邻，因此弧长为 (0,1)；j＝0 表示调车作业必定从连挂钩开始，因此弧长为 (1,0)。j＞k 表示反向弧 (调车前后车组相对顺序相反) 需多增加一个连挂钩和一个溜放钩来调整顺序并使其相邻，因此弧长为 (1,1)。

若已确定连挂钩与溜放钩的费用比重，则易将弧长 (相应的权) 转化为实数。为了讨论选编钩计划中的连挂钩和溜放钩数，研究保留权重为二维向量。为了便于分析和讨论，特定义如下。

定义1：设一个车列 L 的车组排列为 i1,i2,…,in，G(V，E) 是根据上述方法转化得到的有向图，则称 G 为车列 L 生成的有向图。

定义2：设 G 是 i1,i2,…,in生成的有向图，ejk是G 中从点 ij到点 ik的一条有向弧，若 j＜k，则称 ejk为正向弧，若 j＞k，则称 ejk为反向弧。

2.2 最优下落方案问题等同于最小 Hamilton 路问题

观察由车列 L 生成的有向图 G (V，E)，可得到以下结论。

定理1：设G (V，E) 是由原车列 L：i1，i2，…，in生成的有向图，0，I1，I2，…，In，m＋1 是 G 的一条从 0 到 m＋1 的 Hamilton 路，则 I1，I2，…，In对应了调车后的一个可行的车组排列顺序，I1，I2，…，In中的 t 个反向弧将车列分成了 t＋1 节子车列，每个子车列的车组相对顺序在 i1，i2，…，in和 I1，I2，…，In中保持相同。其证明如下。

（1）根据站顺的要求，可行的车组排列顺序为I1，I2，…，In中任意的两点 Ij和 Ik(0＜j＜k＜n＋1)，有 Ij≤Ik。假设存在一条 Hamilton 路对应的调车后的车组排列顺序是不可行的，则必存在一条有向弧 ejk，其中ij＞ik，这与转化条件(2)矛盾，所以Hamilton 路对应的车组排列顺序一定是可行的。

（2）由反向弧的定义可知0和 m＋1 不可能是反向弧的起点，可设 t 个反向弧的起点分别是 Ij1，Ij2，…，Ijt，则车列被分成的 t＋1 个子车列为：0，…，Ij1；Ij1+1，…，Ij2；…；Ijt+1，…，m＋1。每个子车列中只包含正向弧，对任意正向弧在原车列中为 ejk( j＜k)，在编成的车列中为 ej'k'(k '＝j'＋1，j'＜k ' )，显然相对顺序保持不变。

定理 2：设G (V，E，C )是由 i1，i2，…，in生成的有向图，0，I1，I2，…，In，m＋1 是 G 的一条从 0 到 m＋1 的 Hamilton 路，总长为 (a,b)，则存在a 个连挂钩和 b个溜放钩的选编钩计划，将i1，i2，…，in调整为 I1，I2，…，In。其证明如下。

根据 G (V，E，C) 的生成条件可知正向弧0→j1的弧长 C0j1＝(1，0)，其余正向弧长为 (0,1)或 (0，0)；反向弧长为 (1，1)，由此可得反向弧的个数为 a－1，其将车列分成的子车列数目为 a，弧长为 (0，1) 的弧的数目为 b－a，除 (0，0) 弧外的正向弧的数目为 b－a＋1。因此，可按以下方法进行调车。

为每一个反向弧分成的子车列分配一条线路，将待编车列所在线路分配给 i1所在子车列。

将车列迁出 (i1及其 (0，0) 弧连接的车组坐底)，将各车组溜放到相应子车列的线路内，其中(0，0) 弧的终点车组随其起点车组一起溜放，这样每个除 (0，0) 弧外的正向弧和反向弧的端点车组各发生1个溜放钩，由于 i1不可能是 (0，0) 弧的端点车组，因此 i1由于坐底节省1个溜放钩，此过程共发生1个连挂钩和 b－a＋1＋(a－1)－1＝b－1个溜放钩。

依次连挂除 j1所在子车列外的所有车组，并将其溜放到 j1所在线路即完成调车作业，此过程共发生 a－1 个连挂钩和一个溜放钩。

整个调车作业共发生 a 个连挂钩和 b 个溜放钩。需要注意的是，在线路不受限的情况下存在通过 a 个连挂钩和 b 个溜放钩完成调车任务，但其不一定是最优的调车方案。

定理 3：求原始车列为 i1，i2，…，in的最优调车后的车组排列顺序等价于求有向图 G (V，E，C)的0到 m＋1 的最小 Hamilton 路。其证明如下。

由定理1可知，每条从0到 m＋1 的 Hamilton 路对应着一个可行的车组排列顺序，由定理2可知，可以通过该 Hamilton 路长 (对应的连挂钩和溜放钩)完成调车作业，因此有定理 3。

3 模型的转换与求解

求一个有向图的最小 Hamilton 路是一个 NP 困难问题，当车组数较大时，一般很难求最优解。但是，待编车列生成的有向图具有一定的特性，利用该特性可将求有向图 G 的最小 Hamilton 路问题转化为求 一个有向图的最短路问题。

由于编组有站顺要求，因此所求的 Hamilton 路具有以下特性：只有当同一个到达站的车组节点全部经过后，才能进入下一个到达站的车组节点；而当同一个到达站的车组节点的进入节点和离开节点确定后，根据生成图的弧长取值可知，通过所有该到达站节点的最小 Hamilton 路的顺序必定是第一个点为进入节点，最后一个节点为离开节点，而其他节点的顺序与在原车列中的排列相同。按照此方法即可将问题转化为最短路问题，而最短路问题则较容易求解。

例如，某到达站的各车组在原车列的排序为：1，3，5，7，9，若已知进入节点为 7，离开节点为 1，则最小Hamilton 路经过该到达站的各车组节点顺序为：7，3，5，9，1。即 3，5，9 的顺序与原排列相对不变。经过这些点的总长为：(1，1)＋(0，1)＋(0，1)＋(1，1)＝(2，4)。

例如，原车组排列为 2 3 2 1 2 1 3，即第一站车组的顺序为 4、6，第二站车组的顺序为 1、3、5，第三站的车组的顺序为 2、7。则构造最短路图，如图3所示。其中，第2站只标出两个点，中间点未标出。如 1→3 表示 1→5→3，其长为 (0,1)＋(1,1)＝(1,2)。

为反映连挂钩与溜放钩的区别，使用二维向量作为路长，在求最短路时需将二维向量转化为实数进行计算，如定义转化向量为 (5，1)T，表示一个连挂钩的费用是溜放钩的5倍，则路长 (2，1)→(2，1)×(5，1)T＝11。容易求得从节点 0 到节点8的最短路为 0，4，6，3，5，1，2，7，8，总路长为(3,5)。调车步骤 (原车列在③线)：3＋5，2－1，1－1，2－1，1－1，3＋2，2＋2，1－5 或 3＋4，1－1，3－1，1－1，3＋2，1－2，3＋2，1－3。

4 案例分析

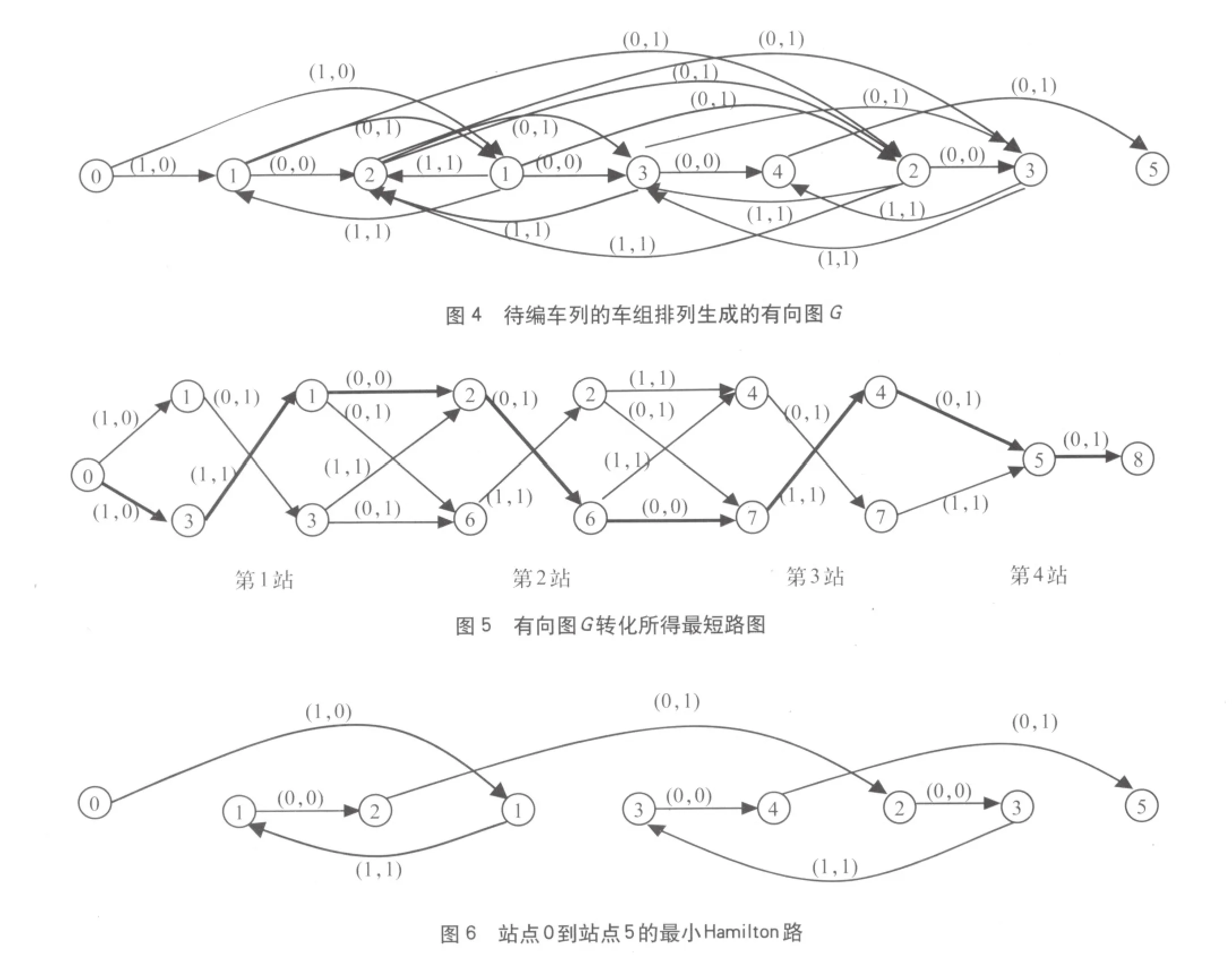
用图论模型分析前述例子，原待编车列的车组排列为 1 2 1 3 4 2 3，其生成的有向图 G (节点数字表示到站序号) 如图 4 所示。

转化所得最短路图 (节点数字表示在原车列中的位置序号，粗线表示最短路径)如图5所示。

从站点0到站点5的最小 Hamilton 路 (节点数字表示到站序号)如图6所示。

路长为 (1，0)＋(1，1)＋(0，0)＋(0，1)＋(0，0)＋(1，1)＋(0，0)＋(0，1)＝(3，4)。则调车后最终的子车列及车组排列顺序为：i3；i1，i2，i6，i7；i4，i5。即相当于原车组的排序为 2 3 1 6 7 4 5，对该车列进行下落，调车步骤为 (原车列在②线)：2＋5，1－1，3－2，2－2，3＋2，2＋4，1－6 或 2＋5，1－1，3－2，2＋2，1－4，3＋2，1－2。如图7所示，为3个连挂钩和4个溜放钩。

图7 车组下落情况

用传统的下落列方法最终的车组排列为 i1，i3，i6，i2，i4，i7，i5，对应于所求的 Hamilton 路如图8所示。

路长为(1,0)＋(0,1)＋(0,1)＋(1,1)＋(0,1)＋(0,1)＋(1,1)＋(0,1)＝(3,7) 需3个连挂钩和7个溜放钩。

5 结束语

传统的下落列方法其算法比较直观、简单，适合手工操作，研究论述的方法虽然较为复杂，但能得到一个确定的最终车组的排列顺序，即一个确定的下落方案，不存在“可调车组”的问题，从而可以简化后续钩计划选优的算法。

该方法转化为计算机程序并不困难，主要面临3个问题：首先，将待编车列转化为有向图，这可以根据有关转换规则较易得到有向图；其次，将同站车组之间的 Hamilton 路简化，根据此 Hamilton 路的特性，也很容易计算和简化有向图；最后，有向图最短路问题的求解已经是个比较成熟的问题，算法和计算机程序并不需要重新设计。因此，研究的方法看似复杂，但是转化为计算机算法的每一步都很简单，很容易实现，同时又可以大大简化后续钩计划选优的算法，提高程序整体的计算效率。

编制选编钩计划时车组的不同下落方案，其实质反映的是调车后同到站车组的不同排列顺序。通过构建图论模型，将求调车后车组的最优排列顺序，转化为求一个有向图的最小 Hamilton 路问题，并利用同一到站的车组经过之后才能进入下一到站这一特性，将求解最小 Hamilton 路问题转化为求一个有向图的最短路问题，从而得到求该问题最优解的有效算法。

研究求得的最小 Hamilton 路的路长，反映的是待编车列中车组排列的规律，并非对应最优选编钩计划中所需的最少连挂钩数和溜放钩数。为求得最优的选编钩计划仍需对由反向弧分成的子车列进行合并等操作。最小 Hamilton 路反映了调车作业车组位置调整的实质，如何通过 Hamilton 路及其正向弧和反向弧的关系来求得最优的选编钩计划，还有待进一步地深入研究。

[1] 徐瑞华，张国宝，徐行方. 轨道交通系统行车组织[M]. 北京：中国铁道出版社，2005.

[2] 曹书波. 调车作业计划优化方法研究[D]. 兰州：兰州交通大学，2003.

[3] 宋建业. 优化筛选摘挂列车编组调车方案的分析计算法[J].铁道学报，1999，21(3)：11-17.

[4] 刘彦虎，周磊山，刘桐飞. 编制摘挂列车调车作业计划的优化计算方法[J]. 铁道运输与经济，2008，30(3)：78-81.

[5] 高四维，张殿业. 一种新的调车作业原理——“消逆法”[J]. 铁道学报，2003，25(5)：1-7.

[6] 李 纬. 摘挂列车调车计划的算法研究及实现[J]. 铁道运输与经济，2007，29(3)：79-81，84.

[7] 李凤义. 提高调车作业效率的对策[J]. 铁道运输与经济，2009，31(5)：89-90.