MIMO下行链路系统预编码技术

南京化工职业技术学院自控系 邓玉茹 施奇铭

一、引言

20世纪80年代以来，全球范围内无线移动通信得到了前所未有的发展。随着各种无限通信业务和宽带数据业务的不断发展，无线资源，尤其是频谱资源变得越来越紧张，如何更高效地利用这些有限的通信资源成为无线通信新技术发展的焦点所在。

传统的无线通信系统是采用一个发射天线和一个接收天线的通信系统，即所谓的单输入单输出系统（SISO）。SISO系统在信道容量上有一个不可突破的瓶颈—shannon容量限制。不管采用哪种调制技术，编码方式或其他方法，无线信道总是给无线通信做了一个物理限制。正是基于这些原因，MIMO（多输入多输出Multiple-Input Multiple-Output）系统已经在许多无线通信系统中得到了广泛的应用。但是相对于SISO（single-input single-output系统，MIMO系统的通信会受到多用户，多天线的干扰，因此在收发机两端需要采用一些必要信号处理技术，以消除噪声和干扰。

针对MIMO下行链路系统，由于基站比移动台具有更强的信号处理，并且基站能够获得估计的信道状态信息，因此可以通过基站首先消除信道对信号的干扰，这一过程称为预编码，即由基站在发射信号前进行预处理来消除多用户干扰。目前，预编码方法主要包括线性预编码和非线性预编码，通常在相同的运算准则下，非线性预编码的性能要好于线性预编码，是目前研究的主流。本文将对已有的非线性预编码进行简介，并重点分析和仿真了其中的矢量预编码，最后提出了未来预编码研究方向和趋势。

二、MIMO下行链路系统预编码技术

图1 脏纸编码算法框图

预编码的主要原理是基站利用接收端反馈的MIMO信道的先验信息，通过预编码矩阵调制MIMO发射信号，灵活地根据信道条件调整并行流的数量，并将能量集中在特定的方向上，以获得最佳的MIMO传输效果。在接收端，移动台只需对信号进行简单的处理就能解出自己所需的信号。由于预编码技术在MIMO下行链路系统中起着重要作用，近年来获得了充分的关注。

当基站已知完全且准确的信道状态信息时，预编码处理的目的是考虑性能改善和提高系统容量，根据算法中是否包括非线性处理，可以分为线性预编码和非线性预编码两类。常见的线性处理方法主要包括基于ZF（迫零）准则、基于MMSE（最小均方误差）准则、以及块对角化等方法。常用的非线性处理方法主要是基于“脏纸编码”思想的各种预处理方案，包括THP预编码及矢量预编码。本节主要介绍常见的非线性预编码。

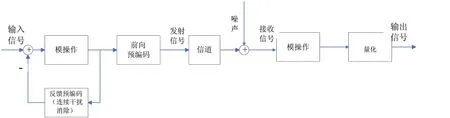
图2 THP预编码算法框图

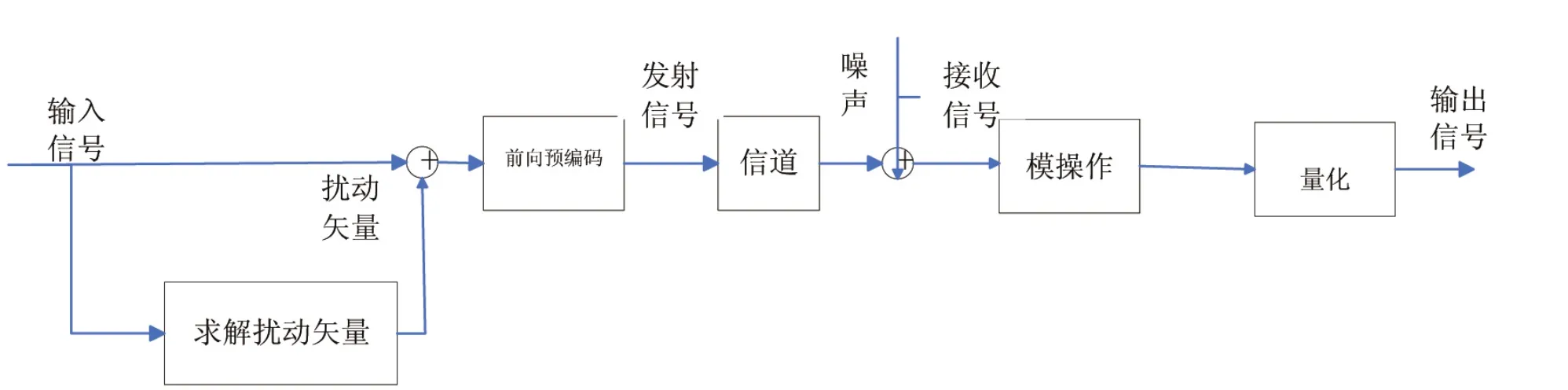
图3 矢量预编码框图

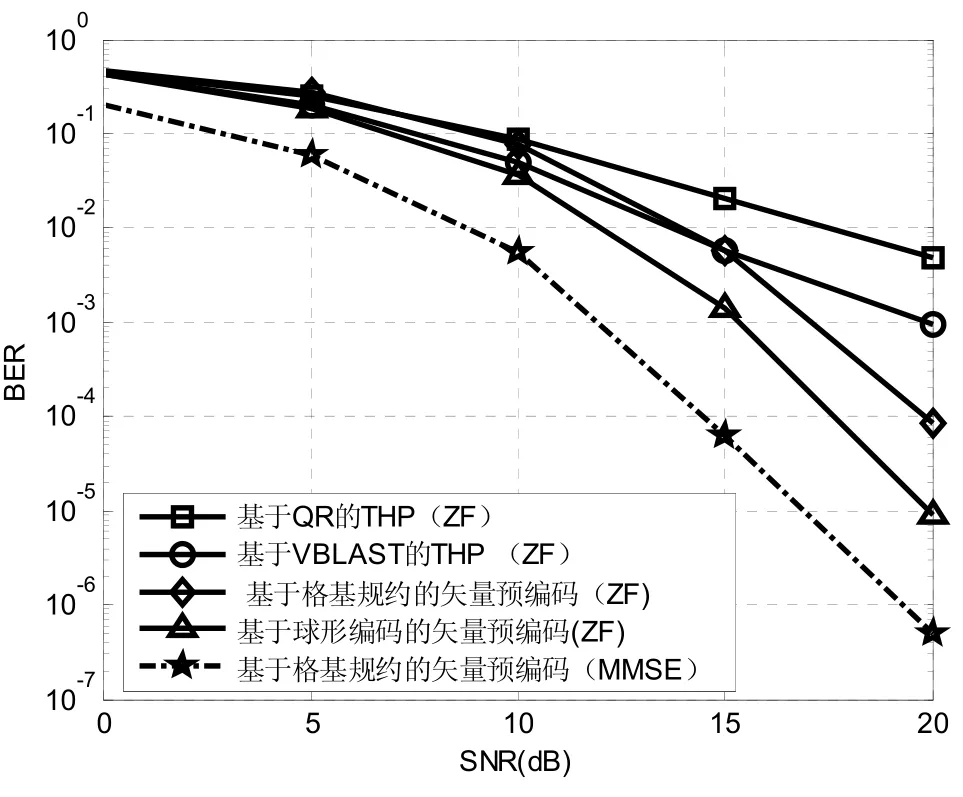
图4 不同非线性预编码算法误码率性能比较（4QAM调制）

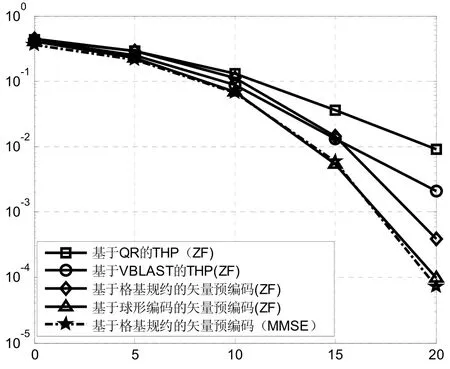
图5 不同非线性预编码算法误码率性能比较（16QAM调制）

1.脏纸编码

“脏纸编码”（DPC），由Costa在1983年那篇著名的论文中首先提出“Writing on Dirty Paper”[1]的思想，他把传输带干扰的信号比喻为在有污点的纸上写字，如果已知污点的位置和大小，那么读者获得的实际信息量等于无污点写字的信息量。如果将传统的加性高斯白噪声信道修改为发送端已知干扰的模型，即：接收信号=发送信号+干扰+噪声，并且在发射端已知干扰的大小，那么可以通过编码的方式在发射端消除干扰，而接收端相当于不受干扰影响。经过这种编码的信道容量，等于无干扰时的信道容量，因此，通过使用脏纸编码理论上能够逼近信道容量。

2.THP预编码

Costa提出脏纸编码的思想，但是并没有给出能够实现逼近信道容量的实际设计方案。文献[2]首先提出了将脏纸编码应用在多用户MIMO下行链路系统中，因为发射端已知信道信息，它能够知道一个用户的信号对其他用户造成的干扰，在设计其他用户的发射信号时就可以把已知的干扰去掉。具体实现这种编码的方法可以采用Tomlinson-Harashima Precoding预编码，它最初用来对抗时域的符号间干扰（ISI），然后被提出用在空域的MIMO系统下来消除多用户干扰。THP实际上是把判决反馈均衡器（DFE）的反馈部分移到了发射端。THP预编码是一个串行过程，经过反馈环节后，第二个用户可以消除第一个用户的干扰，第三个用户可以消除第一个、第二个用户的干扰，依此类推，前面的用户对后面的用户干扰将被消除。

3.矢量预编码

比THP预编码具有更广义的脏纸编码是矢量预编码，文献[3]提出，在原始发射信号向量上加上一个扰动矢量，改变原始发射信号向量的特性，使其发射功率最小化。对扰动矢量的选择，实际上是一个联合优化过程，联合选择最优的扰动矢量中所有元素。从物理意义上讲，由扰动矢量推导出的某个值应反比例于信道逆矩阵的奇异值，当奇异值越大时，这个值越小，奇异值越小时，这个值越大，如果这个值与每个奇异值的乘积近似相等，那么这时的扰动矢量是最优的。这种新的信号成形方法，被称为矢量预编码（Vector Precoding）[4]。它加入一个扰动矢量对发射信号进行成形的编码方式，大大减小了发射信号的功率，从而提高系统性能。在接收端，通过模操作将扰动矢量去除，使扰动矢量并不影响信号的均衡和解调。

矢量预编码的框图如图3。

在矢量预编码中，求解扰动矢量的过程，在数学上可以认为是一个寻找最近格点的问题。对一般的格来说，更常用的方法首先固定一个搜索范围，保证最优点一定在这个搜索范围内，然后在这个范围内的所有格点进行搜索，寻找这个最优点，这样可以大大减小搜索的复杂度，在这类算法中的有限域是平行于基向量的。这类算法有两篇开创性的文献，一是Pohst提出的在超球面范围内寻找格点[5]，另一篇是Kannan提出的在平行六面体内寻找格点[6]，后续文献对这两种方法进行了修改和扩展研究。Kannan列举算法虽然复杂，但是它提出了一种重要的思想，即把最近格点搜索算法分为两步来实现，第一步是将已知的格进行变换，使其基向量变得更短更正交，这个过程我们称为“格基规约”，当格的基向量变得更为正交时，在格中搜索最近点，将比原来的格速度更快。所以算法的第二步就是在一定范围更正交的格中搜索最近点。

在这个思想下，文献[7]对格基规约算法进行了较为全面的描述，并将它与Babai近似算法相结合，找到格中的近似最近点，并且算法的复杂度大大降低。最常用的格基规约算法是LLL算法，LLL算法分为两步实现，第一步是规约基的长度，通过对基向量的映射和加重处理，使基向量的长度变短；第二步是基向量交换，因为格基规约的目的是使所有基向量的长度乘积最小，但是仅进行基向量长度变短的处理，并不能使所有长度的乘积最小，实际上，长度越小的基向量越在产生矩阵的后端，如果把产生矩阵的基向量进行较为均匀的排序，那么能够减小基向量长度的乘积，所以第二步实际上是一个排序过程，比较前后基向量的长度，若后面的基向量长度较短，就将其与前面的基向量交换，若后面的基向量长度大于前面的基向量，就不进行处理，通过排序，将较短的基向量排到产生矩阵的前面。但是，排序后的基向量又影响了基向量的长度特性，所以第一步和第二步应循环进行，由第二步的结果又放入第一步重新处理，如此循环往复，直到所有基向量满足特定的收敛条件，循环结束，得到格基规约后的基向量（产生矩阵），这就是LLL算法的基本过程，这个处理过程是多项式复杂度的。除LLL算法可以进行格基规约外，还有深度搜索LLL算法，整数LLL算法，Seyen算法等多种格基规约算法，每种算法都有各自的特点和适合的应用范围。

4.预编码技术的研究趋势

预编码技术的研究是发展新一代无线通信所面临的一项长期任务，针对实际系统的应用以及性能的提升，未来预编码技术的研究将向以下几个趋势发展：

（1）降低反馈量的预编码研究。在预编码中发射端需要已知信道状态信息，若将信道矩阵进行全反馈，将占用大量的系统资源，不符合实际使用的要求。因此，为了达到实际系统的应用，需要进一步研究在不降低预编码性能的前提下，降低信道状态信息的反馈量，或者将信道信息反馈与多用户MIMO系统下行链路预编码进行联合设计，提升系统容量。

（2）研究复杂非理想信道条件下的预编码设计，由于非理想CSI（信道状态信息）模型较为复杂，产生误差的原因有多种，在问题推导过程中常会出现非凸函数，求解具有难度，目前已有的研究并没有完全解决复杂非理想CSI模型下的系统性能问题。因此，深入研究复杂非理想CSI条件下的鲁棒非线性预编码，对于提升实际传输系统中的性能，具有重要的意义。

（3）考虑将MIMO系统预编码技术应用在多小区干扰消除方向，通过多个基站间的信息和数据交互，将多个基站视为等效的MIMO发射系统，即虚拟MIMO系统，使用预编码方法消除小区间干扰，是LTE-A系统考虑的小区干扰消除的主要方法之一。

三、仿真分析

图4和图5分别给出了文中列出的几种非线性预编码算法仿真结果，其中THP预编码算法分别使用QR分解和VBLAST算法实现预编码反馈，矢量预编码求解扰动矢量分别采用格基规约算法和球形编码算法求解，并且仿真了基于MMSE准则的格基规约矢量预编码算法。图4使用4QAM调制，图5使用16QAM调制。

从图中可以看出，由于VBLAST算法能够对THP预编码中串行干扰消除环节进行排序，能够优先消除干扰较大的用户干扰，因此性能优于QR分解的THP预编码。而矢量预编码是对THP预编码的扩展，改变了原始发射信号向量的特性，使其发射功率最小化，因此分集增益大于THP预编码算法，即满分集增益。基于球形编码的预编码算法性能优于格基规约算法的矢量预编码，但是复杂度是呈指数级上升的，折中算法的性能和复杂度，格基规约算法更适合实际应用。最后，基于MMSE准则的矢量预编码算法性能优于ZF准则，因为ZF准则更容易受病态信道的影响。

四、结论

本文概述了目前主流应用MIMO下行链路系统中的非线性预编码算法，包括脏纸编码，THP预编码和矢量预编码，并重点说明了矢量预编码中格基规约算法的思想。根据对已有的算法概述，提出了未来预编码的研究方向和发展趋势。最后，对几种典型的非线性预编码算法进行了计算机仿真，仿真结论表明基于MMSE准则的格基规约矢量预编码算法性能较好，可以达到满分集增益。

[1]M Costa.“Writing on dirty paper.”IEEE Trans.Information Theory,vol 29,no3,1983,pp:439-441.

[2]G.Caire and S.Shamai,“On the Achievable Throughput of a Multi-Antenna Gaussian Broadcast Channel,”IEEE Trans.Info.Theory,vol.49,July 2003,pp.1691-1706.

[3]Feng Liu,Lingge Jiang,Chen He.“Low complexity lattice reduction aided MMSE precoding design for MIMO systems.”

[4]Bertrand M.Hochwald,Christian B.Peel,A.Lee Swindlehurst,”A Vector-Perturbation Technique for Near-Capacity Multiantenna Multiuser Communication—Part II:Perturbation.”IEEE.TRANSACTIONS ON COMMUNICATIONS,VO L.53,NO.3,MARCH 2005,pp:537-544.

[5]M.Pohst,“On the computation of lattice vectors of minimal length,successive minima and reduced bases with applications,”ACM SIGSAM Bull.,vol.15,Feb.1981.pp.37-44.

[6]R.Kannan,“Improved algorithms for integer programming and related lattice problems,”in Proc.ACM Symp.Theory of Computing,Boston,M A,Apr.1983,pp.193-206.

[7]Wai Ho Mow.“Universal lattice decoding:principle and recent advances.”Wireless communications and mobile computing.pp:553-569.