商场客流量B—J方法预测研究
何文阁
(南通航运职业技术学院基础教学部,江苏 南通 226010)
商场客流量B—J方法预测研究
何文阁
(南通航运职业技术学院基础教学部,江苏 南通 226010)
利用时间序列分析的B—J方法,建立商场客流量ARMA预测模型。根据预测模型,对商场的客流量进行预测,并通过预测的客流量数据与实际客流量数据检验模型的适用性和有效性。
客流量;时间序列;B—J方法;预测
0 引言
客流通常也被称为人流,是大型商场、购物中心等公共场所在管理和决策方面不可缺少的数据。客流的研究对于依赖于客流的产业来说意义重大。尤其是对于零售业来说,客流更是非常基础的指标。顾客是货币的携带者,又是商品的潜在购买者,研究客流量规律,可以增加销售机会,将观看者转变为购物者,最大限度地挖掘商场的销售潜力,增加利润。
客流量统计预测研究的重要性主要表现在以下几个方面:
①通过客流量统计预测,为商场管理者决策提供理论依据。
②通过客流量统计预测,可以有效评估所举行的营销和促销投资的回报。
③通过客流量统计预测,可以计算客流人群转化率,提高商场服务质量;可以计算客流人群购买力,提高营销和促销的效率;可以计算客流人群的平均消费能力,进而预测商场和店内经营者的盈利能力。
④通过客流量统计预测,可以分析本商场在同类商场中的客户占有率和消费者关注度,进而分析商场所处的地位,为与其他同类商场的竞争提供科学的理论依据。
1 B—J方法预测客流量的原理及方法
1.1 B—J方法及预测原理
B—J方法是20世纪60年代由美国统计学家Geogre.E.Box(博克斯)和英国统计学家 Jenkins(詹金斯)提出的一套关于时间序列分析、预测和控制的方法。被称为Box—Jenkins方法,简称为B—J方法。B—J方法是一种平稳时序线性模型法,其核心为自回归移动平均模型(Auto-Regressive Moving Average Model),简称 ARMA模型,是一种精度较高的时间序列预测方法。
B—J方法预测的基本原理是:某些时间序列是依赖于时间的一组随机变量,构成该时序的单个序列值虽然不具有确定性,但整个序列的变化却有一定的规律性,可以用相应的数学模型近似地描述,通过对该数学模型的分析研究,能够更本质地反映时序的结构和特征,进而对事物进行预测和控制。它主要解决2个问题:一是时间序列的平稳性、随机性、季节性,二是在对时间序列分析的基础上,选择适当的模型进行预测。
1.2 B—J方法预测模型
B—J方法的预测模型,即ARMA模型表达式为:
Φ(B)Xt=θ(B)at
其中,Xt= α1Xt-1+ α2Xt-2+ … + αpXt-p-β1at-1-β2at-2-…- βqat-q+at;B为用后移算子。α1,α2,…,αp、β1,β2,…,βq和 σ2a共计p+q+1 个未知参数,这些未知参数要利用观测数据进行估计。
1.3 B—J方法建立预测模型的方法和步骤
B—J方法把时间序列建模主要分为模型识别、参数估计、应用模型进行预测3个阶段和以下4个步骤:
第一步 对原始数据进行预处理。对数据进行零均值化和差分平稳化处理。
第二步 相关性分析和模型识别。自相关和偏自相关分析,计算样本自相关函数k和偏自相关函数kk,然后判断自相关函数k和偏自相关函数kk的截尾性和拖尾性,初步确定模型类型。
第三步 参数估计和模型定阶。对初步确定的模型阶数和参数作出判断和估计。参数估计是整个建模的核心阶段。模型参数估计的方法主要有矩估计、最小二乘估计和极大似然估计。本文采用的是矩估计。



为了建立最优模型需要给模型定阶。模型定阶方法主要有残差方差图定阶法、自相关函数(ACF)和偏自相关函数(PACF)定阶法、F检验定阶法、最佳准则函数定阶法(FDE准则、AIC准则、BIC准则)。本文采用AIC准则定阶法。
定义AIC准则函数为:

可逐个取(p,q)为(1,1)、(1,2)、(2,1)、(2,2)计算对应模型的AIC值。AIC值最小的模型为最优模型。
第四步 时间序列预测。时间序列的预测方法,主要有条件期望预测法和几何预测法。本文采用条件期望预测法进行预测。设当前时刻为t,用时刻t及以前时刻的观测值Xt,Xt-1,Xt-2,…对时刻t以后的观测值Xt+l(l>0)进行预测,这种预测称为以t为原点,向后期(或步长)为l的预测,预测值为(l)。用Xt,Xt-1,…对Xt+l的取值进行预测,Xt+1是一个未知的随机变量,可以用其条件期望值作为预测值。由于Xt之间具有相关性,因而Xt+l的概率分布是有条件的(即在Xt,Xt-1,…已给定的条件下),其期望也是有条件的,即:

再根据Xt和at的条件期望的性质,可以得到(l)=E(Xt+l|Xt,Xt-1,…)。对于 ARMA(p,q)模型的序列,可以通过Xt-α1Xt-1-…-αpXt-p=at- β1at-1- …- βqat-q求Xt+l的条件期望,逐一求出(l)。

当l≤max(p,q)时:

式(6)中,当l>q时,滑动平均部分全部消失,有:

2 实例
根据长春东方家园物业部提供的2005年9月18日—2006年9月30日的客流量的数据。利用2005年9月18日—2006年6月23日的275个数据作为时间序列的观测值,建立预测模型,保留2006年6月24日—2006年9月30日的99个数据,作为对建立的预测模型的检验。
第一步 数据的预处理。
①平稳性检验,计算每组数据的均值和方差,如表1所示。
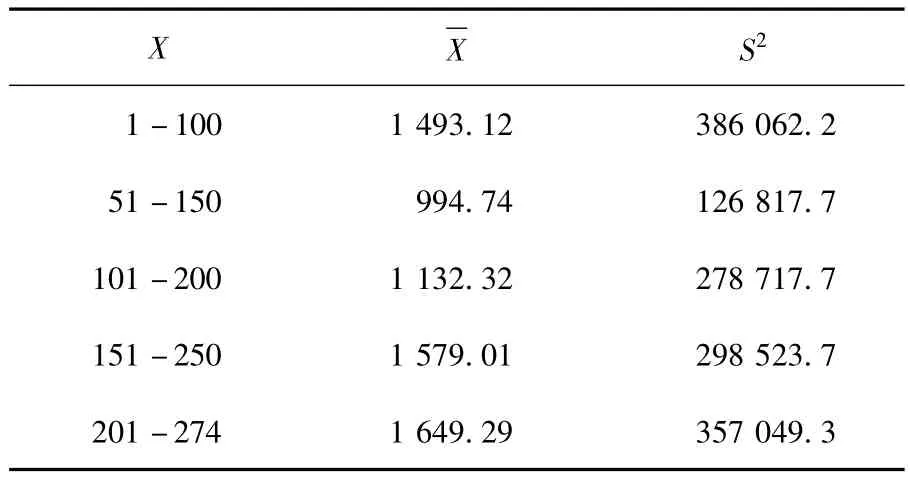
表1 数据平稳性检验表
从表1可以看出,均值和方差的变化差异很大,判断客流量的数据是非平稳时间序列。
(2)数据的平稳化和零均值化处理。采用一阶差分的方法对数据进行平稳化处理,即:

差分后得到的新的时间序列{▽Xt}为平稳时间序列。对平稳化后的时间序列{▽Xt}零均值化,得到零均值平稳的时间序列{Yt}。
第二步 客流量的相关性分析和模型识别。根据自相关函数和偏自相关函数的定义,计算ACF和PACF,如表2所示。

表2 自相关函数与偏自相关函数表

图1 ACF图

图2 PACF图

第三步 参数估计和模型定阶。采用矩估计方法,分别计算出 ARMA(1,1)、ARMA(1,2)、ARMA(2,1)、ARMA(2,2)相应的参数估计值,如表3所示。

表3 ARMA(p,q)模型参数估计表
从表3可以看出,ARMA(2,2)模型的AIC值为最小,根据AIC定阶准则,选择模型ARMA(2,2)来预测客流量。具体模型为:

第四步 客流量的预测。由ARMA(2,2)模型,利用条件期望预测方法,以2006年6月23日为原点向后做99期到2006年9月30日的预测,并与实际客流量进行比较,给出了6月24日—7月23日30 d客流量预测结果数据(见表4)和6月24日—9月30日99 d客流量异常数据统计表(见表5)。
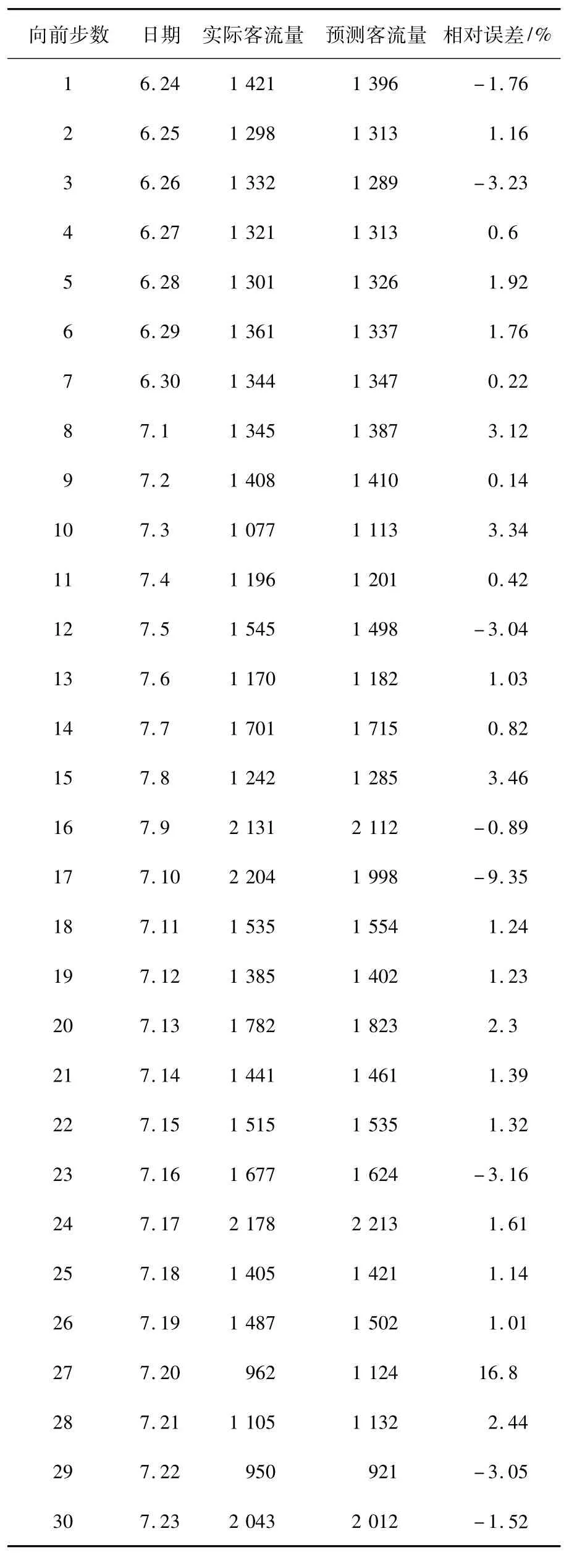
表4 长春东方家园6月24日—7月23日客流量预测结果表

表5 长春东方家园6月24日—9月30日客流量异常数据统计表
3 客流量预测结果分析
从表4可以看出,8月5日的预测结果与实际客流量的偏差最大,预测客流量是1 130人,实际客流量是930人,多预测200人,预测的相对误差为21.51%;7月2日的预测结果与实际客流量的偏差最小,预测客流量是1 410人,实际客流量是1 408人,多预测 2人,预测的相对误差为0.14%;从预测结果上看,除7月10日等13个工作日的预测结果相对误差超过5%以外,其余的预测结果均在5%以内,预测准确率达到87.7%。特别是有33个工作日的预测客流量与实际客流量的相对误差小于1%,预测优秀率达到33.3%。因此,利用ARMA(p,q)模型预测商场的客流量是适用的、有效的。虽然有13个工作日的相对误差超过5%,但是预测值的整体变化趋势与实际客流量的变化趋势是一致的。
经过分析得出,导致相对误差较大的主要原因是:①由于人工计数造成的人为误差。②模型中参数计算、模型定阶等带来的误差,属于系统误差。第一方面的误差可以通过提高保安人员的素质得到改善;第二方面的误差是不可避免的,但可以通过精确计算,进一步调整模型中的参数来提高预测的准确率。
[1]王德辉,刘宁.时间序列分析在证券分析中的应用[J].吉林师范大学学报:自然科学版,2008(1):25-29.
[2]赖民,赵世舜,宋立新.关于投资收益—风险模型等价性的证明[J].吉林大学学报:理学版,2003,41(4):454 -457.
[3]王德辉,宋立新,史宁中.序约束下ARCH(0,2)模型参数的估计与检验[J].应用概率统计,2002,18(3):244-254.
[4]孙继湖,彭建萍.时间序列分析技术在煤炭价格预测中的应用[J].地质技术经济管理,2000,22(3):47-51.
[5]王振龙.时间序列分析[M].北京:中国统计出版社,2002.
[6]安鸿志.时间序列分析[M].上海:华东师范大学出版社,1989.
[7]吴今培,孙德山.现代数据分析[M].北京:机械工业出版社,2006.
[8]王吉信,朱孔来.现代经济预测、决策新方法[M].北京:经济管理出版社,1997.
Research on the B—J Prediction Method for Market Passenger Capacity
HE Wen-ge
(Dept.of Basic Courses,Nantong Shipping College,Nantong 226010)
By using time series analysis B—J method,shopping traffic ARMA prediction model is established.Based on the prediction model,the mall traffic is predicted.Through the forecast and actual traffic data,this paper tests the applicability and validity of the model.
customers flow capacity;time series;B—J method;prediction
O212
A
1671-0436(2011)02-0024-05
2011-02-23
国家自然科学基金资助项目(10571073)
何文阁(1966— ),男,硕士,教授。
责任编辑:张秀兰

