基于专家系统的不确定性推理机的研究与实现
陈小玉
(南阳理工学院 计算机科学与技术系,南阳 473000)
0 引言
现实中大多数问题是非精确、非完备和模糊的,具有一定程度的不确定性,因此,关于不确定性推理及其方法的研究就成为人工智能的一个重要课题,并已提出了多种理论和方法[1]。推理机是专家系统的“思维”机构,使得计算机能够运用知识进行推理,求解问题,构成了专家系统的核心部分。本文研究与开发了一套基于专家系统的推理机平台,能够处理多种不同组织形式的知识,对于推理机的设计提出了更高的要求,不仅适用于某一具体专家系统,还具有可扩充性,对于处理不同问题的专家系统,具有实用性、高效性。利用该平台,农业专家可以很方便地输入各种农业知识规则,形成具体的农业专家系统。对于不同结构形式或表现形式的知识,可以选择各自合适的推理机。
1 不确定性推理机
1.1 基本概念
可信度是指人们根据以往经验对某个事物或现象为真的程度的一个判断,或者说是人们对某个事物或现象为真的相信程度。显然,可信度具有较大的主观性和经验性,其准确性是难以把握的。但是,对某一具体领域而言,由于该领域专家具有丰富的专业知识及实践经验,还是完全有可能给出该领域的可信度的。因此,可信度方法不失为一种实用的不确定性推理方法[2]。
以温度,湿度,肥力等级等因素决定选用的辣椒品种为例:
规则1:IF 温度>23度,湿度<8,肥力等级=高 THEN 辣椒品种=辣椒1号。
前提是知识(规则)的前项,一条知识一般包含多个子前提,在规则1中,“温度>23度、湿度<8、肥力等级=高”是该知识的前提项。结论与前提相对应,是知识(规则)的后项,一条知识可能产生多个结论,但在本推理方法中,为了处理上的方便,只产生一个结论。对于多结论的情况,只需进行简单的分解即可。在规则1中,得出的结论是“辣椒品种=辣椒1号”。证据是用户输入的原始事实;结果是推理机从初始证据出发,运用知识,最终推出的合理或者基本合理的最终输出。若用户输入证据为“温度=25度,湿度=6,肥力等级=高”,推理机从这些初始证据出发,运用规则1最终推出结果“辣椒品种=辣椒1号”。
1.2 知识不确定性的表示
在该不确定性推理方法中,知识是用产生式规则表示的,知识的表示形式是:
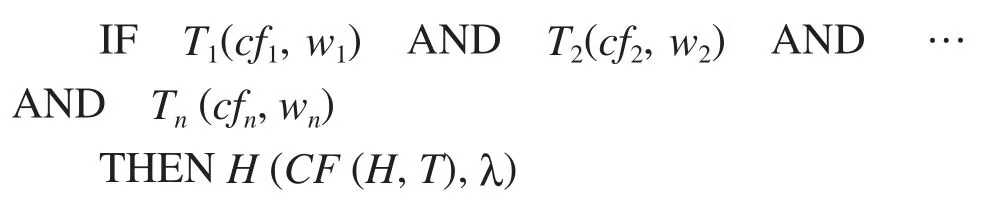
1)子前提Ti(i=1, 2, …, n)是知识的前项。子前提Ti的可信度cfi(i=1, 2, …, n)表示在没有提供任何证据时,前提Ti的真实程度[3]。知识的不确定性采用规则强度CF(H,T)来描述,CF(H,T)是指当规则中的前提为真时结论为真的可信程度,它反映了前提对结论的支持程度,实际上是对规则正确性程度的一个估计值。cfi与CF(H,T)在[0,1]上取值,其值由领域专家给出。
2)wi是子前提Ti(i=1, 2, …, n)的权值,表示子前提的相对重要程度,在[0,1]上取值,且应满足条件:。wi的值由领域专家给出。
3)λ为规则阈值(0<λ<1),其值也由领域专家给出。
1.3 证据的不确定性表示
证据的不确定性也是用可信度因子来表示的,其可信度CF(E)反映了已知事实的确定性程度,在[0,1]上取值。对初始证据E,若对能肯定它为真,则使CF(E) =1;若它以某种程度为真,则使CF(E)取区间(0, 1)中的某一个值,即0<CF(E)<1;若它以某种程度为假,或者不确定,则使CF(E) =0。
1.4 不确定性匹配算法
当知识的前提与相应的证据不完全一致时,可用匹配度来表示两者相似的程度。用相应的不确定性匹配算法检查匹配度是否落在阈值指定的限度内。如果落在阈值指定的限度内,就认为它们是可匹配的,相应的知识可被利用;如果没有落在阈值指定的限度内,则认为它们是不可匹配的,相应知识不可用于当前的推理中。
本文用贴近度来描述匹配度。贴近度是指两个概念或事实的贴近程度,可直接用来做匹配度。设有两个集合A,B,则将式(1)

定义为集合A,B的匹配度。其中:

设对于第k条规则
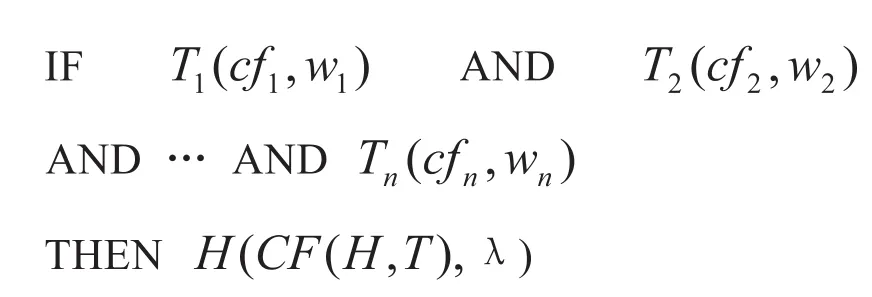
有如下的证据存在:
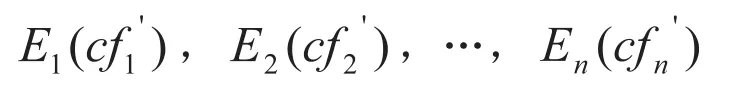
根据公式(1)计算前提项Ti和证据项Ei的匹
配度公式为:
规则匹配度M k(T,E)表示证据集E={E1,E2,…,En}, 与知识库中的第k条规则前提集T k={T1,T2, …,Tn}, 相似的程度,其值由下式计算:

则不确定性算法为M k(T,E)≥λ。当规则匹配度M k(T,E)≥λ时,第k条知识被激活。
1.5 不确定性的传递算法
不确定推理实际上是从不确定性的初始证据出发,不断运用相关的不确定性知识,逐步推出最终结果和该结果的可信度的过程。而每次运用不确定性知识,都需要由证据的不确定性和知识的不确定性去计算结果的不确定性。
通过利用上述的不确定匹配算法,判断出知识的前提条件与相应的证据匹配,则结果的可信度计算公式如下:
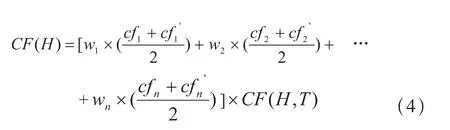
2 推理机的实现
推理机的性能与构造一般与知识的表示方式及组织方式有关[5]。首先简要介绍一下本系统的知识表示及其组织方式。
2.1 知识表示及其组织形式
本系统采用“规则架+规则题”规则组知识表示策略[4],知识库主要包括决策模块表、决策项目表及决策项目-模块管理表和权重表等。决策模块表对应规则组知识表示的规则架,字段主要由前提因素集组成,另外包括用于系统管理、推理的其他信息,各前提因素的不确定性因子也在该表中给出;决策项目表对应规则体,记录包含了因素之间求解的具体指示,可以是运算公式,也可以是一组规则,也记录了知识的可信度、阈值,一个决策模块一般包括多个决策项目;权重表记录知识各前提项的权重;事实表用来存放用户提供的初始事实、问题描述以及系统运行过程中得到的中间结果、最终结果等。
2.2 推理过程
本推理机采用的是以事实作为出发点的正向推理,并结合以可信度为基础的模式匹配和冲突消解策略。假设需要对某问题进行推理,则首先需要向推理输入决策模块和决策项目名,然后根据用户的输入,检查数据表中是否包含了问题的解,若数据表中不存在问题的解,则在决策项目表中检查,检查出可适用的知识,利用上述的推理算法进行推理,直至成功或失败结束。
3 应用实例
利用该专家系统开发平台,可以高效地开发出多个实用的专家系统。现以辣椒专家系统中的辣椒品种选择决策为例,说明推理机的工作过程及算法实现:
1)用户选择决策模块及决策,输入事实证据送入数据表。
2)数据表中包含问题的解?是成功退出,否则转向3)。
3)决策项目表中有适用的知识?是转向5),否则转4)。
4)判断用户可补充新事实,如果有,把用户提供的新事实加入到数据转向3),否则退出。
5)把项目表中所有适用的知识选出来形成可用知识集。
6)判断可用知识集为空,是转向7),否则转向 4)。
7)对各条可用知识进行推理,将推理得出的结果送入结果,从结果集中选出可信度最大的结果,输出,将新事实加入到数据表中。
设决策项目表中有一组知识:(不一定准确,只是为了举例说明)

其中:T1=地区在北方;T2=地区在南方;
T3=土壤肥力等级为高;T4=肥力等级为中;T5=肥力等级为低;
T6=温度大于或等于20度;T7=温度小于20度;
H1=种子为辣椒1号;H2=种子为辣椒2号;H3=种子为辣椒3号
用户输入的一条证据为:
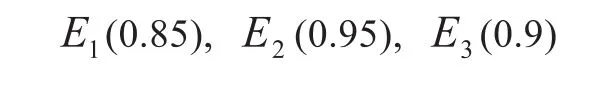
其中:E1=地区在北方;E2=土壤肥力等级为中;E3=温度小于20度
检查决策项目表,判断是否存在可适用的知识。首先检查各条知识,筛选出知识Rule2;第二步根据公式(3),计算匹配度,判断Rule2是否被激发,是否为可适用的知识:

显然,0.4675>0.25,即匹配度M(T,E)大于阈值λ,所以知识Rule2被激活;最后利用Rule2进行系统推理,推理结果为“种子为辣椒2号”,并且根据结果可信度得计算公式(4)得出结果的可信度为:
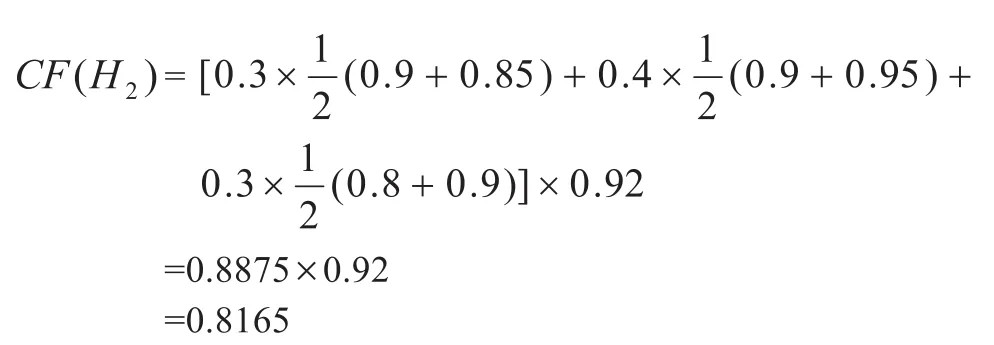
我们利用该专家系统开发平台开发的辣椒专家系统,对上例的推理界面如图1所示。
系统允许有不确定性的因素,譬如肥力等级无法确定,则可以选择?项,系统同样可以进行推理,推导出最有可能的结果。推理中,需要用户输入事实证据及证据的可信度,证据的可信度的默认值为1。
4 结论
本文所提出的不确定性推理算法,结合了可信度方法的基本思想,将其改进使之适合应用于专家系统开发平台的推理机制,从而很大程度上改善了推理机制的性能和效率。

[1] 王永庆.人工智能原理与方法[M].西安: 西安交通大学出版社, 1998.
[2] 王万森.人工智能原理及其应用[M].北京: 电子工业出版社, 2000.
[3] 肖伟跃.模糊规则中的不确定推理研究[J].应用科学学报.2002(3), 94-98
[4] 熊范纶.农业专家系统及开发工具[M].北京: 清华大学出版社, 1999.
[5] Joseph Giarratano, Grary Riley.Expert System Principles and programming.Beijing: China Machine Press, 2000.

