基于不完全评价信息的外包业务供应商选择
孙首群,吴虹江,刘 钢,冯晓刚
(1.上海理工大学 机械工程学院,上海 200093;2.上海宝钢设备检修有限公司,上海 201900)
0 引言
为了决策的科学化、民主化,对于重大的复杂决策问题一般采用群体决策的方式。群决策的结果来自于个人决策,是对个人决策结果的加权、综合过程。多属性群决策解决的问题核心是:如何集结决策群体全体成员的偏好以形成群体的偏好(决策结果)。但是在许多实际问题中,往往由于知识领域的限制,决策群体成员只能对方案的部分属性做出评价,现有研究成果多未充分考虑这种情况[1~3]。
本文以某特大型钢铁企业外包业务的供应商选择策略为对象进行分析和研究。选择策略实现过程面临三方面的困难:一是涉及的因素杂、指标多,各因素间相互影响、相互制约,要对合作伙伴进行准确评估选择是不容易的,往往只能给出模糊的评价[4~8];二是它又不同于一般多目标决策问题,一般需要由多个决策人组成的群体对有限的方案的多个属性(目标)进行评价和选择;三是在生产企业中,各决策人并不能对方案的所有属性做出评估,只能对自己职责内熟知的方案属性做出评价,这是由企业职能分工造成的。
1 问题描述
设X={X1,X2, ,Xm}是方案集,S={S1,S2, ,Sn} (n≥2)是属性集,属性值既可以是定量的,也可以是定性的,并假设这些属性是加性独立的,记ω= (ω1,ω2, ,ωn)T是属性的权重向量,P=(P1,P2, ,Pt) (t≥2)是决策者集,W={W1,W2, ,Wt} (t≥2)是决策者在决策群体中的决策权重向量。Y+= (y1+,y2+, ,yn+)T、Y-= (y1-,y2-, ,yn-)T分别是属性的正负理想值向量。矩阵=[]m×n表示决策者Pk针对方案集X关于属性集S的决策矩阵,其中=(),是三角模糊数。
由于决策问题的复杂性、时效性以及决策者认识的局限性,上述矩阵=(k= 1, 2, ,t)的某列或某几列元素未必能给出。本文将研究属性集某列或某几列未知的情况。
1.1 定量属性指标的规范化处理
定量属性指标可分为效益型指标和成本型指标,效益性指标是指属性指标值越大越好的属性,成本型指标是指属性指标值越小越好的属性。为了保留决策模糊数的不确定性,给出如下公式[9~11]:
效益型属性指标:
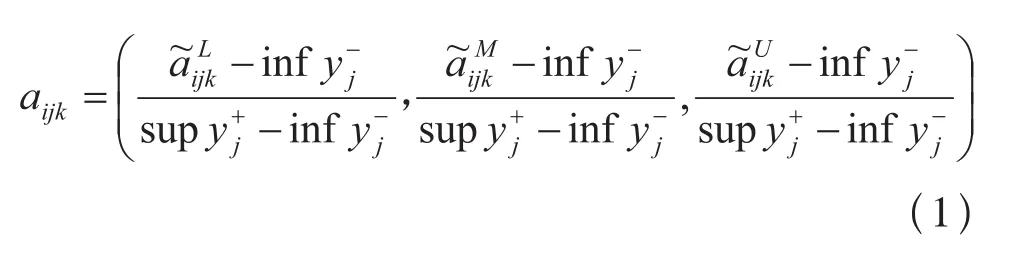
成本型属性指标:
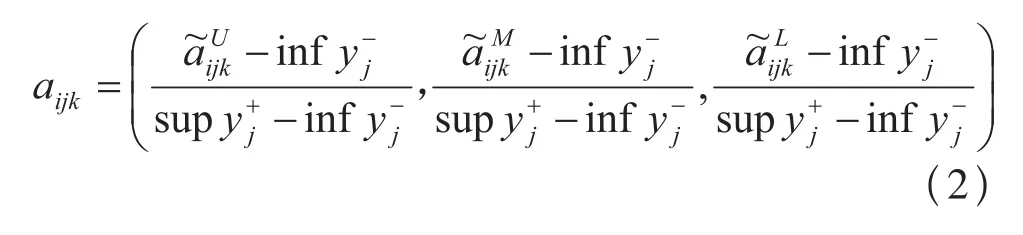
1.2 定性属性指标的规范化处理
心理学家米勒(G.A.Miller)经过实验证明,在某个属性上对方案进行判别时,普通人能正确区别属性的等级在5级到9级之间,即语言指标一般表达为5级到9级评判指标。本文采用5级评判指标(绝对好、好、一般、差、绝对差)对定性属性做规范化处理。
2 问题解析
由于各决策矩阵Ak=(k=1, 2, ,t)的属性值信息不完全,且具有某列或某几列数据全部未知的特征,基于此,本文换一个角度,从属性值的视角考察问题。
首先,汇总所有决策者针对每一个方案,在每一个属性下的属性值信息,形成mn个集合。比如,设已知aijk是决策者Pk针对方案Xi依据属性Sj给出的决策值,那么所有在属性Sj下的决策值,就可以形成新矩阵ASj=[aijk]m×n,该矩阵囊括了在属性Sj下对方案集Xi=(i=1, 2, ,m)做出决策的所有可能决策者的决策信息;记矩阵ASj中元素的个数为mn′,由于可能只有部分决策者对属性Sj做出了决策,所以信息不完全,也就有可能存在0≤n′≤n的情况。本文研究n′≠0,即ASj非空的情况。
然后,矩阵 ASj= [aijk]m×n′(0≤n′≤n)实质是决策群体中的部分成员针对各方案依据属性Sj做出的决策结果,根据各决策成员的决策权重,利用加权的方法可得出该部分成员针对各方案依据属性Sj做出的群决策结果,其结果形成一个集合Bj={b1j,b2j, ,bmj}T,其中元素bi=(,,)i{1, 2, ,m}是该决策群体中的部分成员针对方案Xi依据属性Sj做出的群决策结果,是一个三角模糊数。依次计算针对各属性的群决策结果,得到一个模糊规范化决策矩阵:

最后,按照下列步骤对模糊规范化决策矩阵B进行处理:
1)对模糊规范化决策矩阵B=[bij]m×n进行加权:

2)对正、负理想方案各属性指标值加权:

3)计算各方案与正(负)理想方案的模糊距离:

其中,
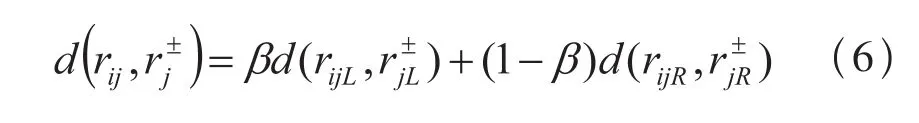
β表示决策的不确定偏好系数,当β=0.5表示决策者为不确定中性者;β>0.5表示决策者为不确定厌恶者;β<0.5表示决策者为不确定喜好者。
4)计算各方案与正理想方案的相对贴近度:
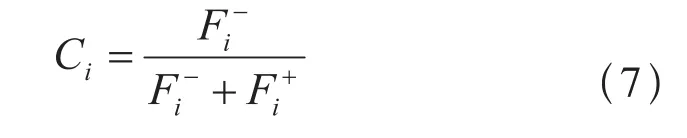
5)按照Ci由大到小排列,前面的方案优于后面的方案。
3 案例分析
本文综合已有的研究成果[12~15],在对企业实际经营状况广泛调查研究的基础上,经反复推敲,最后提出了适用于制造业务外包供应商评价与规则的指标体系,该指标集合包括:S1=投递准确度、S2=装运质量、S3=产品价格、S4=制造能力、S5=顾客服务、S6=产品创新、S7=产品研发时间、S8=质量管控力度、S9=文化创新、S10=财务状况等10项指标。
设现有三家供应商X={X1,X2,X3}可供选择,拟从中选取一家作为长期合作的制造业务外包供应商。公司内部组建了从各部门抽调的经验丰富的工作人员组成的4人决策组P={P1,P2,P3,P4}针对三家供应商的属性集S={S1,S2, ,S10}分别做出评价。各属性的权重信息如表1所示。
其中,S3、S7和S8为成本型指标,其余为效益型指标,各属性的正负理想值分别为:(1,0),(非常好,非常差),(120,250),(非常强 ,非常弱 ),(非常优秀,非常恶劣),(非常强,非常弱),(1,4),(0,0.2),(1,0.8),(非常好,非常差),即:
Y+=(1.0,非常好,120,非常强,非常优秀,非常强,1.0,0.0,1.0,非常好)

表1 各属性的权重
Y-=(0.0,非常差,250,非常弱,非常恶劣,非常弱,4.0,0.2,0.8,非常差)
已知决策群体成员的决策权重如表2所示:

表2 决策成员决策权重
利用前述给出的模糊语言-模糊数转换规则将模糊语言转换成模糊数并进行规范化,并依次计算针对各属性的群决策结果,得到一个模糊规范化决策矩阵B,如表3所示。
假设决策群的不确定厌恶系数β=0.8。
按式(3)-(7)计算得各方案的相对贴近度分别为:
C1=0.77;C2=0.72;C3=0.68
因此,各方案的排序为:X1>X2>X3。方案X1为最优决策方案。
4 结论
本文研究了如何利用模糊多属性群决策方法对外包业务中供应商进行综合评估和选择。针对决策群体各成员对属性评价有局限性且方案属性值为三角模糊数的模糊多属性决策问题,建立了特定的决策模型,通过对模型的求解获得决策群体对各方案基于各属性的规范化决策矩阵,利用模糊理想点方法对给出的方案进行排序和择优的决策方法。该方法很好的解决了决策过程中决策群体成员评价能力的局限性问题,具有较高的应用价值。
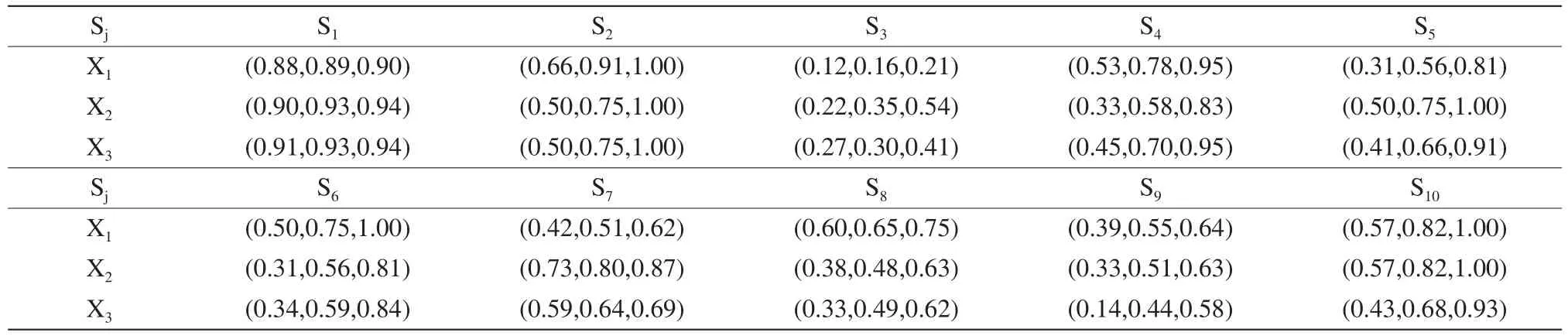
表3 模糊规范化决策矩阵B
[1] 周文坤, 武振业, 刘家诚.模糊偏好条件下多目标群决策的方法[J].西南交通大学学报, 2001, 36(3): 232-234.
[2] Li D F, Yang J B.Fuzzy linear programming technique for multi-attribute group decision making in fuzzy environments[J].Information Sciences, 2004, 158: 263-275.
[3] Cafer E B, Cengiz Kahraman, Da Ruan.Fuzzy group decision making for selection among computer integrated manufacturing systems[J].Computers in Industry, 2003, 51(1): 13-29.
[4] 苏世彬, 黄瑞华.基于三角模糊数的属性层次模型[J].系统工程理论与实践, 2006, (12): 115-119.
[5] 钱存华, 张琳, 戴槟, 等.三角模糊数的加权平均及其在评价决策中的应用[J].运筹与管理, 2005, 14(2): 5-9.
[6] Lin Y H, Lee P C, Chang T P et al.Multi-attribute group decision making model under the condition of uncertain information[J].Automation in construction, 2008, 17(6): 792-797.
[7] Zhao H X, Yang J P, Wan J.Evaluation Model of Credibility of E-Commerce Website Using Fuzzy Multi-Attribute Group Decision Making: Based on Fuzzy Structured Element[J].Fuzzy Information and Engineering, 2010, 78: 417-424.
[8] 徐泽水.基于期望值的模糊多属性决策法及其应用[J].系统工程理论与实践, 2004, (1): 109-113.
[9] Moosung Jae, Joo Hyun Moon.Use of a fuzzy decision-making method in evaluating severe accident management strategies[J].Annals of Nuclear Energy, 2002, 29(13): 1597-1606.
[10] 孔峰, 刘鸿雁.基于决策者不确定偏好的模糊多性决策方法[J].华北电力大学学报, 2005, 32(4): 52-55
[11] 陆华, 杨家其.模糊排序及启发式算法在物流中心选址中的应用[J].武汉理工大学学报, 2002, 26(3): 389-392.
[12] Choy K L, Lee W B.A generic supplier Management tool for outsourcing manufacturing[J].Supply Chain Management:An International Journal, 2003, 8(2):140-154.
[13] 霍佳震, 马秀波, 朱琳婕.集成化供应链绩效评价体系及应用[M].北京: 清华大学出版社, 2005.
[14] 赵京梅, 杨志辉.模糊多属性群决策在铁路系统评价中的应用[J].华东理工大学学报, 2010, 33(2): 187-191.
[15] 桑圣举, 王炬香, 杨阳.基于模糊多属性群决策的供应商分类方法研究[J].机械设计与制造, 2008, (2): 226-228.

