内蒙古“金三角”地区能源消费与经济增长关系研究——基于面板数据的协整分析
孟 军
(1.内蒙古财经学院 统计与数学学院,内蒙古 呼和浩特 010051;2.东北财经大学,辽宁 大连 116025)
引言
内蒙古是我国北方重要的能源大省,尤其是地处内蒙古“金三角”地区的呼和浩特市、包头市、鄂尔多斯市,简称“呼包鄂”,以其突出的能源优势为内蒙古经济社会的快速发展做出了重要贡献,经济实力雄踞自治区之首。与此同时,经济社会的发展越来越受到资源环境的约束,环境问题、能源与经济问题比较突出。能源是经济发展的重要保障因素,如何有效地利用能源对于解决环境问题、能源与经济等问题,保持经济的持续稳步增长具有重要意义。
一、计量模型的建立与检验
(一)计量模型的建立
在经济学中,经济增长可以用生产函数来刻画。生产函数是表示在一定的技术条件下生产投入与产出之间的一种数量关系。本文应用扩展的柯布-道格拉斯(Cobb-Douglas)生产函数来刻画生产过程,即:Y=AKαLβEγ(Nerlove ,1965) (1)
其中Y表示产出,A表示生产要素投入效率,K表示资本投入,L表示劳动力投入,E表示能源投入,α、β、γ分别表示资本、劳动力和能源的弹性系数。与传统的柯布-道格拉斯生产函数Y=AKαLβ(2),简称C-D生产函数相比可以发现,Nerlove在原有C-D生产函数结构的基础上增加了和能源投入有关的乘子。假设用这两个函数对同一生产过程进行解释,则可以看出Nerlove生产函数的本质含义,就是将原本分摊在资本和劳动力要素中的能源因素的影响从C-D生产函数中剥离出来,形成独立的第三要素。在当今社会,由于能源因素在生产过程中的重要性日渐增大,在研究生产过程中忽略能源的影响将会产生很大的误差,所以对CD生产函数加以改进是正确的。考虑到参数估计的方便性和经济学意义,我们对所采用的经济变量都取自然对数形式,并建立如下计量模型:
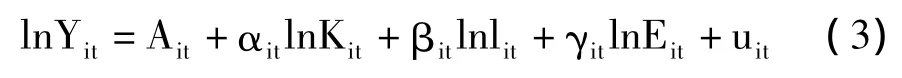
其中,i指地区,t指时间。若 Ait= δ,αit=α,βit=β,γit=γ(δ,α,γ 为常数,uit~ i.i.d.(0,σ2u)),则为混合回归模型。若 Ait=δ+λi,αit=α,βit=β,γit=γ(δ,α,γ 为常数,uit~ i.i.d.(0,σ2u)),则为个体固定效应模型;若 Ait=δ+ηt,αit=α,βit=β,γit=γ(δ,α,γ 为常数,uit~i.i.d.(0,σ2u)),则为时点固定效应模型;若 Ait=δ+λi+ηt,αit=α,βit=β,γit=γ(δ,α,γ 为常数,uit~i.i.d.(0,σ2u)),则为个体时点固定效应模型;若 Ait=δ,αit=α,βit=β,γit=γ,uit=ut+wit(δ,α,γ 为常数,ut为第 t时点的随机干扰项,wit~ i.i.d.(0,σ2w)),则为时间随机效应模型;若Ait=δ,αit=α,βit=β,γit= γ,uit=ui+vt+wit(δ,α,γ为常数,ui,vt分别为个体和时点的随机干扰项,wit~ i.i.d.(0,σ2w)),则为个体时间随机效应模型。若Ait=δ,αit=αi,βit=βi,γit= γi(δ,α,γ 为常数,uit~i.i.d.(0,σ2u)),则为个体固定参数的变系数回归模型(SUR模型);若Ait=δ,αit=¯α+ξαit,βit=¯β+ξβit,γit=¯γ+ξγit(其中ξαit,ξβit,ξγit是均值为0,具有固定方差的随机变量,uit~ i.i.d.(0,σ2u)),则为个体随机参数的变系数回归模型(Swamy模型);若 Ait=δ,αit=¯α+ξαi+Ψαt,βit=¯β+ξβi+Ψβt,γit=¯γ+ξγi+Ψγt(其中 ξαi,Ψαt,ξβi,Ψβt,ξγi,Ψγt是均值为 0,具有固定方差的随机变量,uit~ i.i.d.(0,σ2u)),则为时点个体随机参数的变系数回归模型(Hsiao模型)。
(二)面板数据的单位根检验
由于经济变量普遍存在着非平稳的特征,所以同时间序列类似,在面板数据的分析中,首先也要做平稳性检验,即单位根检验,否则非平稳的面板数据对另一非平稳的面板数据进行回归容易产生伪回归问题,其标准的t和F检验是无效的。通过蒙特卡洛(Monte Carlo)实验发现,与单变量时间序列的单位根检验相比较,各种面板数据单位根检验都不同程度地提高了单位根检验的检验功效。目前面板数据单位根检验的方法比较多,其中Eviews6.0中支持的有:(a)Levin,Lin&Chu t*检验(LLC检验);(b)Breitung t-stat检验;(c)Im,Pesaran and Shin W-stat检验(IPS检验);(d)ADF -Fisher Chisquare检验;(e)PP-Fisher Chi-square检验。其中(a)(b)检验是基于同质面板数据的,(c)(d)(e)检验是基于异质面板数据的。对于LLC检验,允许面板单位根检验式中含有飘移项、时间趋势项。尽管LLC检验是应用最广泛的面板单位根检验,但LLC检验也有局限性,该检验严重依赖于截面的独立性假设,存在纵剖面相关的面板数据不可用,另外,假设所有纵剖面有或者都没有单位根。针对于LLC检验这一缺陷,IM、Pesaran和Shin提出了异质面板的IPS单位根检验,IPS检验允许纵剖面时间序列有单位根,通过蒙特卡洛实验发现IPS检验比LLC检验具有更良好的有限样本的性质。但IPS检验同样具有缺陷,即其要求数据是平衡面板数据,对于非平衡面板数据则无法处理。针对于LLC检验和IPS检验的不足,基于异质面板数据又出现了ADF-Fisher Chi-square检验和PP-Fisher Chi-square检验。对于Breitung检验,较LLC检验和IPS检验更优于具有个体特征趋势项的检验。
(三)面板数据的协整检验
自Engle和Granger(1978)发现时间序列的协整回归以来,有关经济变量间协整关系检验方法的研究已经成为非经典计量经济学理论方法研究的核心问题之一。众所周知,时间序列观测数据的长度直接关系到协整关系检验的效果,经济变量的观测数据越长,协整检验的功效就高,即协整检验过程中犯第二类错误的概率就越小(Pedroni,1995)。然而由于实际研究环境的限制,在许多经济问题的研究中,经济变量的时间序列很短,所以制约了协整理论的发展。于是面板数据的协整理论便应运而生。面板协整检验是用来检验变量间长期均衡关系的。其可分为两类,一类是基于面板数据回归式残差数据单位根检验,即Engle-Granger(1987)两步法的推广。另一类是从推广Johansen检验的方向发展的面板协整检验。相对于前一类检验,后者的协整检验不仅能够检验多个协整关系,而且允许面板数据存在平稳或非平稳的共同成分。其中Eviews6.0支持的有:(a)Pedroni(Engle-Granger based)检验;(b)Kao(Engle-Granger based)检验和(c)Fisher(Combined Johasen)检验。其中(b)是针对于同质面板数据的,(a)和(c)是针对于异质面板数据的。本文采用(b),对经济增长(LnY)和资本投入(LnK)、劳动力(LnL)以及能源消费(LnE)同时做协整检验。
(四)面板数据的误差修正模型及其因果检验
协整的重要特征是它们的时间路径是通过相对于长期均衡的离差大小来影响的。毕竟,如果一个系统恢复到长期均衡,则至少有一些变量的变化一定会对非均衡的大小做出响应。
这类将均衡离差的影响纳入系统短期动态变化过程中的模型称为误差修正模型(Error Correction Model,ECM)。ECM的思想可简单概括为,某一时期出现的非均衡将在下一期予以修正。在协整关系成立的前提下,可建立如下面板数据误差修正模型:
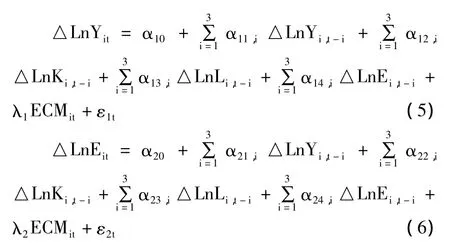
在(5)式和(6)式中,Δ表示一阶差分运算(下同),ECTit表示长期均衡误差。误差修正模型为研究变量之间的因果关系开辟了新途径。在(5)式中,如果α14显著异于0,则能源消费是经济增长的短期Granger原因;如果λ1显著不为0,则能源消费是经济增长的长期Granger原因。反之,如果α14显著等于0,则能源消费不是经济增长的短期Granger原因;如果λ1显著等于0,则能源消费不是经济增长的长期Granger原因。同理,可检验经济增长是否是能源消费的长期或短期Granger原因。
二、实证分析
(一)样本选择与数据描述
本文各经济指标的数据主要来源于《内蒙古统计年鉴》(2002-2011),数据区间为2001-2010,指标的选取与处理如下:
1.国内生产总值Y:通过Y指数平减,化成以2001年为基期的不变价的Y,剔除了价格因素的影响(单位:亿元)。
2.资本存量K:本文采用每年年底实际库存与新增固定资产投资总额(I)的和作为每年的实际资本存量。为使数据具有可比性,使用官方公布的固定资产投资价格指数,通过I指数平减,把每年的新增固定资产投资总额化成以2001年为基期的不变价的。计算每年资本存量时,将t时期的资本存量定义为t-1时期资本存量加投资减折旧,即:

(7)式中,Kit是i地区t年的资本存量,Iit是i地区t年的新增固定资产投资总额,δ是固定资产折旧率。根据历史数据,固定资产折旧率平均在5%左右,因此2001年以来的固定资产折旧率都定为5%。另外,以2001年的固定资产投资总额作为初始资本存量。以后年份的资本存量都按(7)式计算而得到(单位:万元)。
3.全社会职工工资总额作为劳动力L:本文使用全社会职工工资总额作为劳动力资本。这里不是用从业人员人数作为劳动力变量数据,是因为人数变化只能反应劳动力数量的变化,但不能反映劳动力质量的变化,而劳动力作为影响产出量的一大要素最主要的原因是劳动力质量的变化对产出量有很大影响(国涓,2008)。在使用职工平均工资这一数据时,也同样要考虑数据的可比性,以2001年为基期,换算成不变价的职工工资总额(单位:万元)。
4.能源消费总量作为能源E:考虑到近年来中国能源生产和消费总量中,煤炭和石油供需存在明显低估。相比之下,由计算机直接读出的电力消费量数据就相当准确。此外电力消费是中国能源消费的主要方式。因此,使用电力消费更能准确反映能源消费与经济增长之间的内在联系(林伯强,2003),所以本文采用2001-2010年各地区电力消费量作为能源消费量(单位:亿千瓦小时)。
(二)面板数据单位根检验
因为我们所建立的模型是线性模型(取对数后),所以先要检验数据的平稳性,即先对各个变量进行单位根检验。可以说面板数据的单位根检验也是进行面板协整检验分析的必要前提。根据前面介绍的单位根检验方法,利用Eviews6.0我们对呼包鄂地区的国民生产总值的(Y)和资本(K)、劳动力(L)、能源消费(E)的自然对数序列(分别记为LnYit、LnKit、LnEYit、LnLiti)进行了单位根检验,看它们是否是单位根过程,即检验它们各自的平稳性。考虑到呼包鄂地区在经济总量等方面的相似性,我们采用同质面板的Levin,Lin&Chu t*检验即LLC检验(见表1)。
通过对 LnYit、LnKit、LnEYit、LnLiti序列的检验,在5%的显著水平上,序列水平值均不平稳,一阶差分序列均平稳,则可以进行协整检验了。

表1
(三)面板数据的协整检验
首先,我们来建立计量经济学模型。考虑到呼包鄂地区在经济总量等方面的相似性,我们建立同质面板数据的计量模型。至于是固定效应模型还是随机效应模型,我们可以用Eviews6.0提供的似然比检验(即F检验)的方法来确定。下面进行个体时点固定效应模型的设定检验:
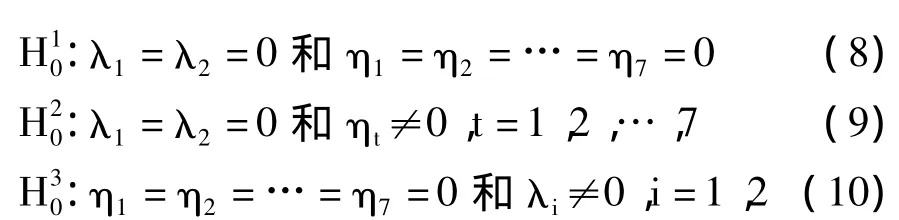
显然,检验假设(9)的目的是推断存在时点效应的情况下,判断模型是否包含个体效应;检验假设(10)正好与上相反。于是,在(8)假设下
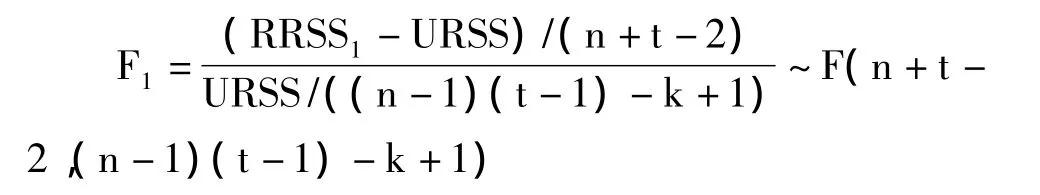
其中,RRSS1为无约束的残差平方和,RUSS为混合回归残差平方和,n=3,t=8,K=1。
同理,在假设(9)、(10)下可分别建立:
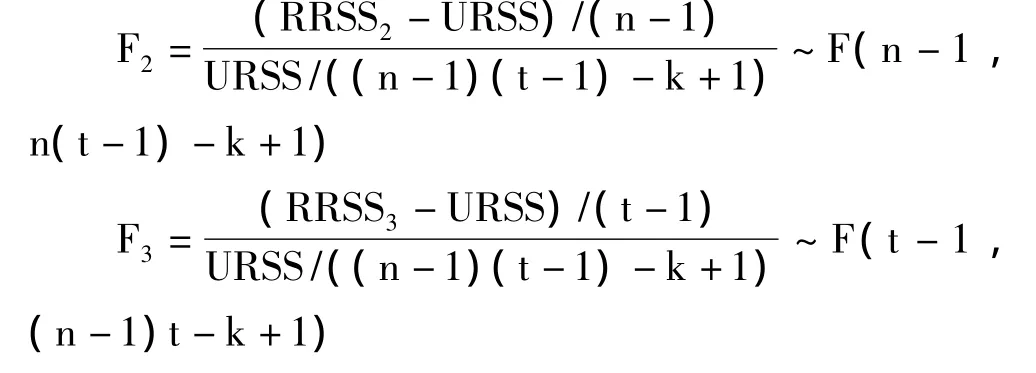
其中RRSS是受约束的回归残差平方和,URSS为无约束的回归残差平方和,k为待估参数个数(不包括常数项)。按照Hendry的“一般到特殊”的建模思想,通过计算得:F1=26.57 >F(9,14)=2.12 ,所以拒绝假设(8),建立个体时点的混合固定效应模型,即:

其中个体固定影响效用为:呼和浩特-0.11,包头 -0.36,鄂尔多斯0.47。
时点固定影响效用为:

2001 2002 2003 2004 2005 2006 2007 2008-0.26 -0.22 -0.09 -0.12 -0.03 0.17 0.22 0.33
下面对上述已经建立的计量模型依Eviews6.0进行协整检验。采用Kao检验,t统计量的值为-2.23,所以在5%的显著性水平上,拒绝原假设(原假设为序列不存在协整),所以序列LYit和LKit、LEYit、LLiti具有协整关系。
(四)面板数据的误差修正模型及其因果检验
通过面板数据协整检验,我们建立了两个协整方程,但由于时间跨度较小,需通过误差修正模型来进一步检验两个协整方程的可靠性。先根据(5)式检验呼包鄂地区能源消费是否为经济增长的Granger原因,再根据(6)式检验呼包鄂地区经济增长是否为能源消费的Granger原因。作为满足误差项经典假设的要求,将滞后项m定为1。在以经济增长为因变量的误差修正模型(5)中,ECM项回归系数λ1为0.18,其t值为2.11,在10%的显著性水平下不为0,所以误差纠正机制发生;而变量△LnEt-1的回归系数α14在10%的水平上显著为0,所以对呼包鄂地区来说,在长期,能源消费是经济增长的Granger原因,而在短期则不是。同理,在以能源消费为因变量的误差修正模型(6)中,ECM项回归系数 λ2为 0.44,其 t值为0.27;变量△LnEt-1的回归系数 α24为 -1.68,其 t值为 -1.09,所以经济增长无论短期还是长期都不是能源消费的Granger原因。
三、结论
通过对能源消费与经济增长的关系进行了实证分析,我们发现能源消费是经济增长的单向Granger原因。进入新世纪,尤其是“十五”以来,呼和浩特、包头和鄂尔多斯能源消费分别由2005年的1416.65万吨标准煤、2380.10万吨标准煤和1300.66万吨标准煤增至2010年的2373.93万吨标准煤 、4018.3万吨标准煤和2704.37万吨标准煤,涨幅近80%;煤炭消费量分别由2005年的2363.14万吨和1765.53万吨、2466.33万吨增至2010年的3637.47万吨 、3823.23万吨和4332.43万吨,涨幅也达到了80%。能源强度由2005年1.90吨标准煤/万元、2.80吨标准煤/万元和2.19吨标准煤/万元下降到1.47吨标准煤/万元 、2.01吨标准煤/万元 和1.59吨标准煤/万元,但下降幅度却只有近30%。这充分说明相对能源利用效率降低了。能源利用效率的降低意味着资源环境压力的增大,因此,提高能源利用效率,不仅有助于释放经济发展潜力,还可以解决经济社会发展越来越受到的资源环境问题。
[1] 林伯强.电力消费与中国经济增长——基于生产函数的研究[J].管理世界,2003,(11).
[2] 马超群,储慧斌,李科,周四清.中国能源消费与经济增长的协整与误差校正模型研究[J].系统工程,2004,(10).
[3] 韩智勇,魏一鸣,焦建玲.中国能源消费与经济增长的协整性与因果关系检验[J].系统工程,2004,(22).
[4] 周少甫,闵娜.中国经济增长与能源消费关系的协整分析[J].当代经济,2005,(6).

