多元回归模型在东风闸过闸流量率定中的应用
孟 健
(杭州市水文水资源监测总站,浙江 杭州 310016)
1 东风闸概况
东风闸位于上塘河余杭区与海宁市交界处的河道断面上。闸门经过2009年翻新改造,现由南北两边孔闸门与一中孔闸门组成,呈对称布置。两边孔闸门较小,尺寸均为3.20m×1.00 m(宽×高),中孔闸门尺寸为5.80 m×2.95 m(宽×高),属小(2)型水闸。在闸上游约50 m和下游约300 m处均设立水尺以观测河道水位。
2 公式建立与率定
由于东风闸建造在平原区河道上,闸上下游水头差一般较小且变幅有限。通过实测,共获取13份闸门不同启闭状态下的过闸流量资料。通过水力学方法分析,3孔闸门的出流方式较为复杂,边、中孔集孔流、堰流、自由、淹没等出流方式于一体且组合方式多变。若单纯采取传统的水力学方法依次对3孔闸门进行过闸流量率定,工作繁琐且对实测资料的数量要求较高。为此,采用多元回归方法,对过闸流量影响因子的选配与处理、计算公式的建立、相关系数的的推求等进行了探析。
2.1 水力学堰闸流量公式
2.1.1 宽顶堰过流公式

式中:Q为过堰流量,m3/s;C为综合流量系数;B为堰宽,m;H为堰上水头,m。
2.1.2 孔流出流公式
闸孔出流有自由出流与淹没出流2种方式,相对应的出流公式如下:

式中:σ为淹没系数;μ为流量系数;e为闸门开度,m;B为闸门宽度,m;H为堰上水头,m。
2.2 相关因子选配与回归方程式建立
回归分析与相关分析法是寻求事物随机变量之间所存在的某种必然的、特殊的约束性即规律性的一种数学处理方法与技术[2]。把需要获取的数据当作因变量 (此文中为过闸流量),把相关因子当作自变量,建立相关关系式。建立的相关关系式也称回归方程式。
通过分析东风闸出流方式,结合水力学堰闸流量计算公式,可以看出闸门过闸流量受闸上下游水头、闸门开度、闸门宽度等因素影响。由于此闸构造为边、中孔共存的形式,可依据各扇闸门的面积为权重,计算出水闸的综合水头,如下式所示:

式中:H综为水闸闸上综合水头,m;Hi、Ai为各扇闸门的闸上水头与闸门面积,m、m2;A总为各扇闸门的总面积,m2。
依据各扇闸门的宽度为权重,计算出水闸的综合开度,如式(4)所示,各实测资料对应的计算值见表1。

式中:e综为水闸综合开度,m;ei、Bi为各扇闸门的开度与宽度,m;B总为各扇闸门的总宽度,m。这里需要说明的是,如果闸门拉起不接触水面(即过闸水流为堰流),闸门有效开度可按照ei=0.65H上计算,式中H上为闸上水头,m。
以H综、Δ Z、e综为相关影响因子,参照水力学堰闸基本流量推算公式,尝试建立多元回归方程式,如式(5)所示:

式中:K、a、b、c 为多元回归系数,Δ Z=Z上-Z下为闸上下游所观测的河道水位差,m。
2.3 多元回归系数的率定
对建立的多元回归方程式做简单变换,然后对方程式两边取对数,得式(6)如下:

通过变换把非线性回归方程转换为线性回归方程,带入实测值计算各测次中的相关变量(见表1)。利用Excel软件中LINEST函数 (线性回归方程参数求解函数)计算出各多元回归系数的值,得出过闸流量推求公式(7):
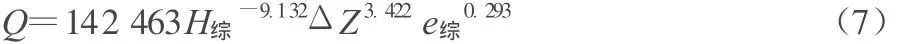

表1 东风闸过闸流量多元回归分析成果表
3 成果检验
闸流量与各相关影响因子的回归分析,建立回归方程只是一种假定,是否符合实际情况就必须进行检验。
3.1 相关性分析
通常,在统计检验中,利用复相关系数R来刻划所建立的回归模型中因变量与自变量的相关程度。0<R<1,愈趋近于1表明相关程度越高。R值的计算公式如式(8)所示:

式中:S总为总离差,S回为回归离差,S剩为残差。经计算所得,本次所建立的回归方程的复相关系数为0.97,回归方程中过闸流量与各相关影响因子中的相关程度较高。
3.2 显著性分析
对回归方程进行显著性检验,是为了证实总体样本中因变量与自变量是否存在线性回归关系。通常使用检验法,方程显著检验见表2。
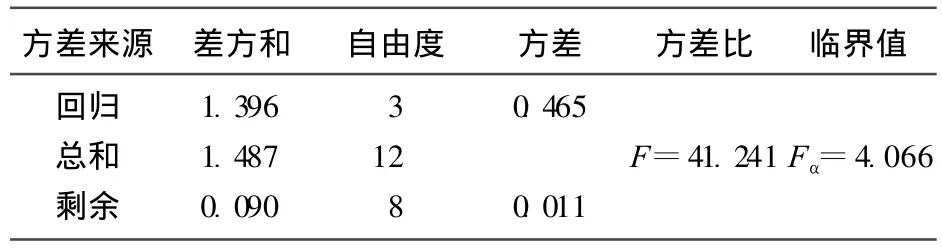
表2 回归方程方差检验表 (α=0.05)
从表2可知,F>Fα,本次推求过闸流量的回归方程可通过显著性检验。
4 结 语
传统的堰闸公式法推求过闸流量,对流态的考虑比较充分,需要很详尽的实测资料作为支撑[4]。同时需要在实际工作中对闸门各种不同调度情况下进行大量流量测验,且闸门出流状态判断也有一定难度。采用多元回归方法推求过闸流量则不需要对流态做过多的研究。本文中对东风闸过闸流量推求成果与实际测定的流量相差较小,可以满足平原区水量调度的要求。
在进行多元回归分析的过程中,自变量选择是很重要的。对过闸流量的影响因子很多,选取方法也千差万别,有待作进一步研究。
[1]李炜,徐孝平.水力学 [M].武汉:武汉水利电力大学出版社,2000:207-305.
[2]袁宇.多元回归分析法在突发性事故污染预测中的应用[J].辽宁城乡环境科技,2002,22(3):19-21.
[3]黄振平.水文统计学 [M].南京:河海大学出版社,2003:221-261.
[4]周全,吴伟华,杨晓斌.上海浦东水闸过闸流量和水量率定方法研究[J].水利水文自动化,2010(1):65-68.

