谐波齿轮几何模型参数优化及ADAMS仿真研究

田 林， 徐世杰

（北京航空航天大学宇航学院，北京 100191）

控制力矩陀螺由于其提供力矩大、输出力矩连续、不污染光学设备等优点，已经成为许多航天器高精度姿态控制执行机构的首选。框架低速驱动控制是控制力矩陀螺系统关键技术之一，在驱动电机和框架之间加装谐波齿轮减速器能使电机工作在相对较高转速范围内，降低了电机转速控制的负担，有助于提高整星姿态控制精度。

谐波传动是上个世纪中期应空间技术要求发展起来的新型传动技术，其理论基础为薄壳弹性变形。1955年，第一台用于火箭的谐波传动装置问世；1959年，美国人C W Musser取得了第一个谐波传动的技术专利。我国从上世纪六十年代开始谐波传动的研究，于 1993年编写制定了“谐波传动减速器国家标准”[1]。谐波齿轮包括激波器、柔轮、刚轮三个主要部件，通过柔轮的微小变形来传递运动和动力。由于具有传动比大、传动精度高、承载力矩大、能在密闭空间使用等诸多优点，谐波齿轮已经在普通精密设备中得到广泛应用。谐波齿轮在航天领域里的应用则集中在大型结构件（太阳能帆板、大功率天线等）的低速驱动方面。谐波齿轮结构紧凑，部件运动和动力传递过程复杂，单从理论上理解比较困难。

滚珠活齿谐波齿轮结构简单，制造成本低，应用广泛。通过几何模型的建立和分析可以了解其运行原理，本研究参考的型号几何参数不全，可以以稳定传递运动为目标对关键参数进行一定优化，全面确定所涉及的几何参数。上海交通大学的宋立博等人建立了谐波齿轮局部啮合数学模型，提出了得到连续啮合仿真图形的方法[2]。北京工商大学的辛洪兵等人对谐波齿轮研究很深入，建立了谐波齿轮系统仿真软件，并以XB-80-134H型谐波齿轮为例给出了仿真结果，对转速误差的频率成分进行了深入分析[3]。武汉理工大学的张佑林等人利用 Pro/ENGINEER建立了端面活齿谐波齿轮模型，直观反映了该型谐波齿轮的运行原理[4]。这些仿真研究集中于几类谐波齿轮，对滚珠活齿谐波齿轮涉及甚少。ADAMS为美国 MDI公司开发的机械系统动力学仿真分析软件，具有丰富的零件库、约束库及可施加载荷，仿真结果以数据、图表及动画的方式输出[5]。在ADAMS中建立滚珠活齿谐波齿轮的原理模型，一方面能够直观地展示其运动原理，另一方面可以通过仿真数据分析与前述几何模型进行相互验证，为以后建立控制力矩陀螺系统模型打下基础。

1 几何模型及参数优化

本研究所参考的滚珠活齿谐波齿轮基本几何模型及尺寸如图1所示。由于减速比大于1，令波发生器为输入轮，活齿采用滚珠，滚珠保持架固定，滚珠只能在径向移动，刚轮为输出轮。图中各个尺寸的含义及符号如表 1所示。表 1中，参数R1、R2和R3不能准确确定，需要通过一定的数值优化计算最终确定。

将图1转换成为示意图，如图2所示。初始时刻为T0，波发生器（输入轮）以转速ω1绕O转动，刚轮（输出轮）以转速ω2绕O转动。T1时刻，输入轮转过 θ1角，输出轮转过 θ2角，图中其它符号含义如表2所示。

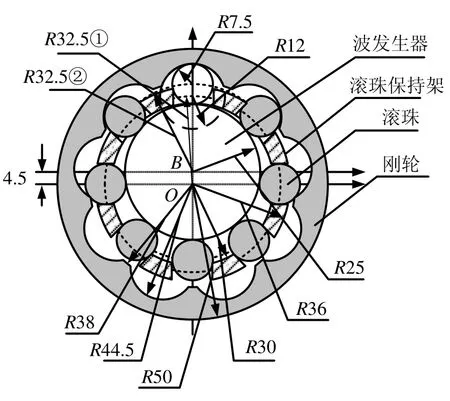
图1 谐波齿轮几何模型及尺寸

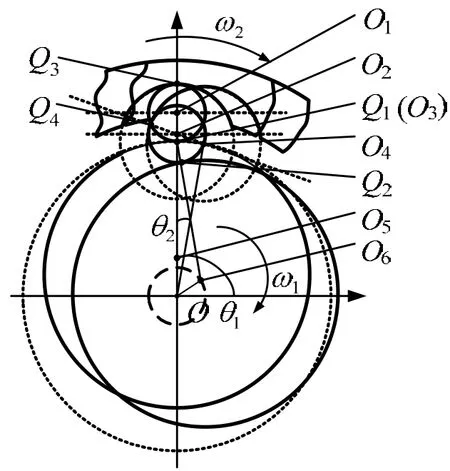
图2 谐波齿轮模型示意图

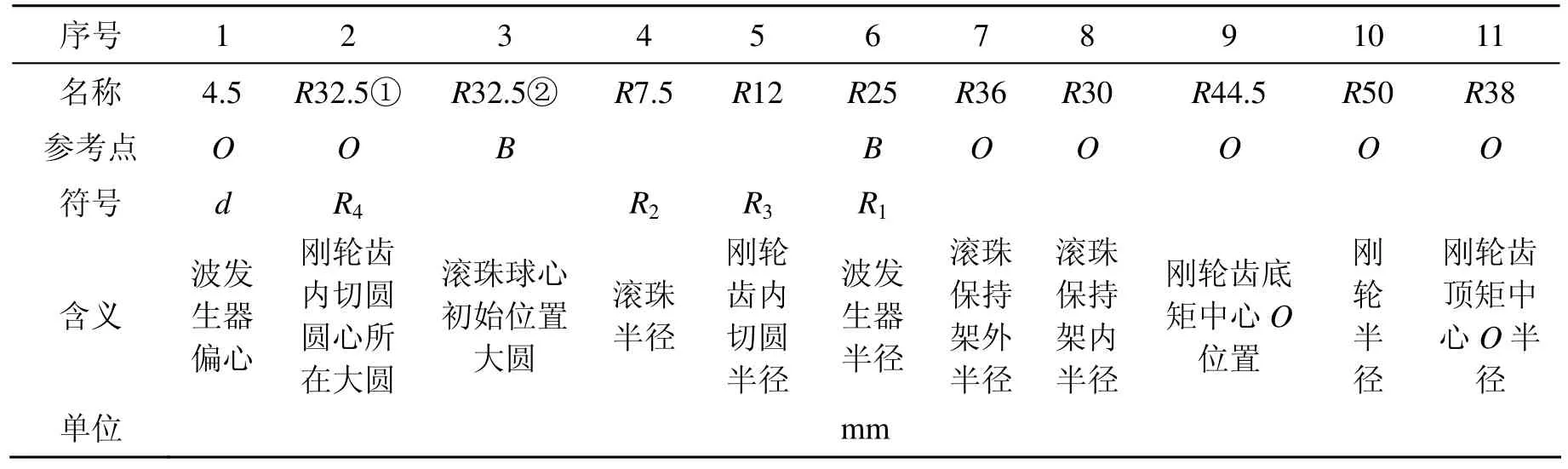
表1 谐波齿轮几何模型符号含义

表2 谐波齿轮模型示意图符号含义

在2θ满足一定条件时，式(5)能够成立，所以取

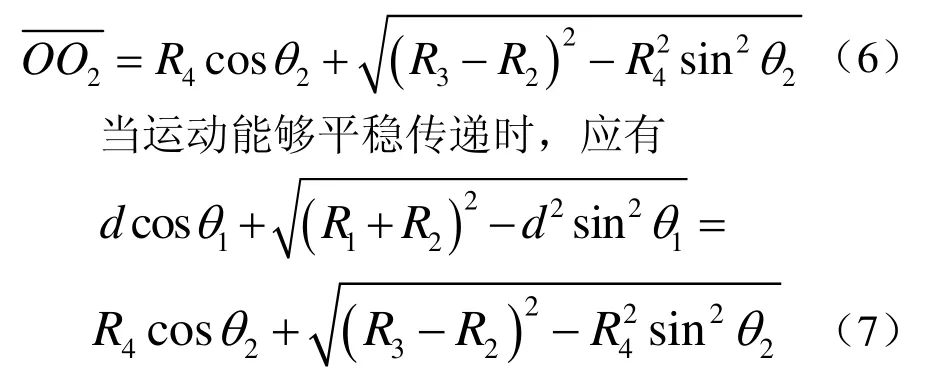
由式(2)和式(6)可以确定滚珠与波发生器外切角（图2中1θ）及滚珠与刚轮齿内切角（图2中2θ）的取值范围

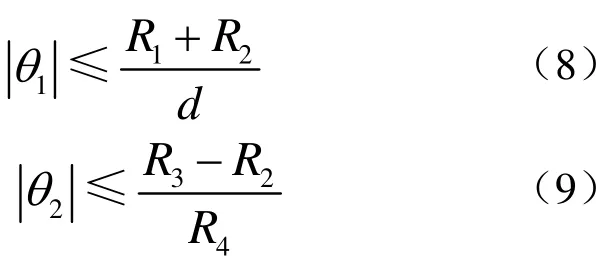
由于 d ≪R1+R2，则θ1取值不限。而R3-R2与R4比较接近，则θ2取值范围较小，这一结论与滚珠活齿谐波齿轮的减速和啮合特性是相符的。

由于表1中参数R1、R2和R3和减速比都没有准确确定，则通过一定的数值计算来确定。以表1的数据为基础，减速比设定在5到25之间，误差指标设为

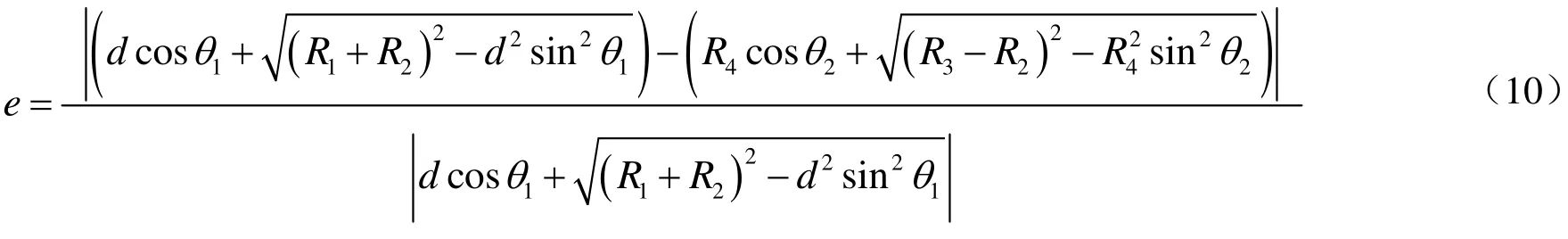
通过数值仿真得到减速比与e之间的关系，如图3所示。可以看出减速比在9附近时，误差能够取得最小，为了计算方便，减速比取整数为9。

以减速比9为基础，对参数R1、R2和R3进行优化，根据图1所示几何关系R1、R2应该满足

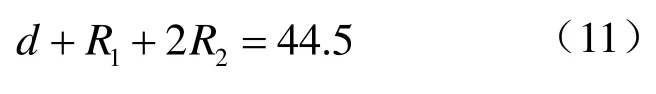
通过数值仿真得到R2、R3与e之间的关系，如图4所示。分析仿真数据得到，当R2=7.5mm，R3=12mm 时，误差 e取得最小值为 1.59×10-4，这一结果说明前一步确定减速比所使用的参数R2、R3取值的合理性。

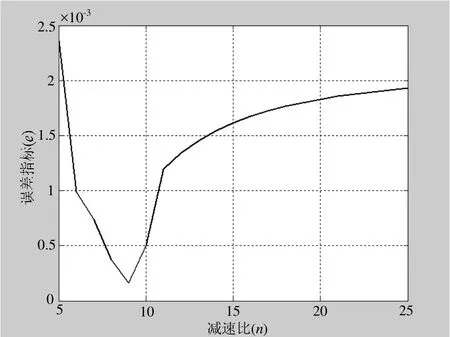
图3 减速比与误差指标关系

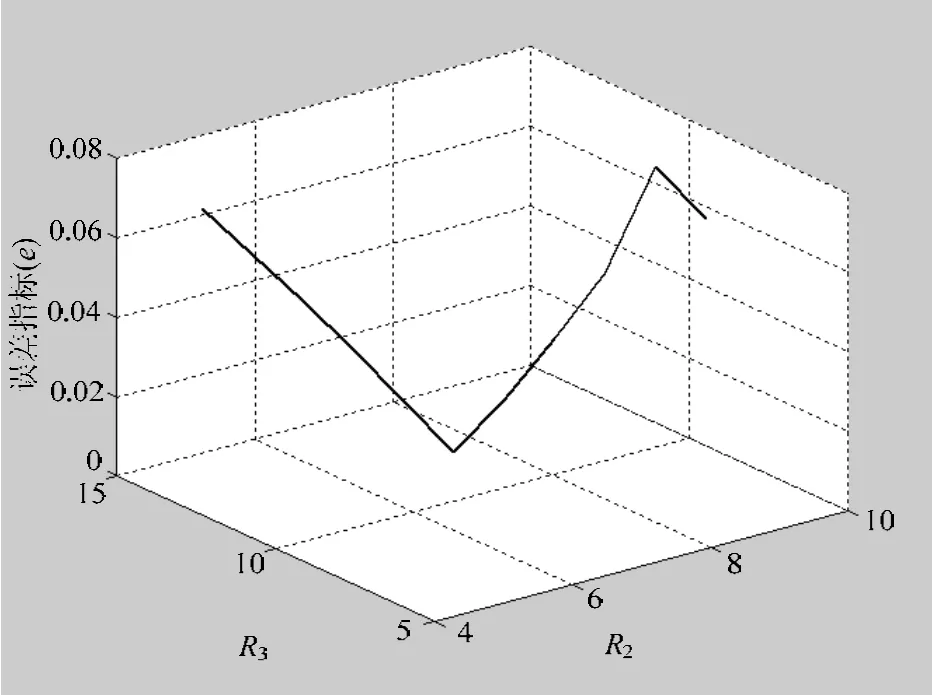
图4 R2、R3与误差指标关系

2 ADAMS模型及仿真

根据前述滚珠活齿谐波齿轮的几何模型和确定的几何尺寸，直接在ADAMS中建立原理模型。造型具体细节为：

（1）主要部件波发生器、滚珠、滚珠保持架、刚轮均采用钢材材质；

（2）滚珠与保持架之间定义两种约束：圆柱约束和球铰约束；

（3）滚珠与波发生器之间定义接触力：刚度系数标准值取1×105N/m，非线性系数取2.2，粘滞阻尼系数取 10，最大阻尼时变形深度取0.5mm；

（4）滚珠与刚轮之间定义接触力：刚度系数标准值取1×105N/m，非线性系数取2.2，粘滞阻尼系数取10，最大阻尼时变形深度取0.5mm。

ADAMS模型框架如图5所示，实体如图6所示。在此基础上进行数值仿真。由于滚珠活齿谐波齿轮结构非常紧凑，且装配时有一定的预紧力，相关刚度系数较大，则仿真步长尽量取小，可取为0.001s。

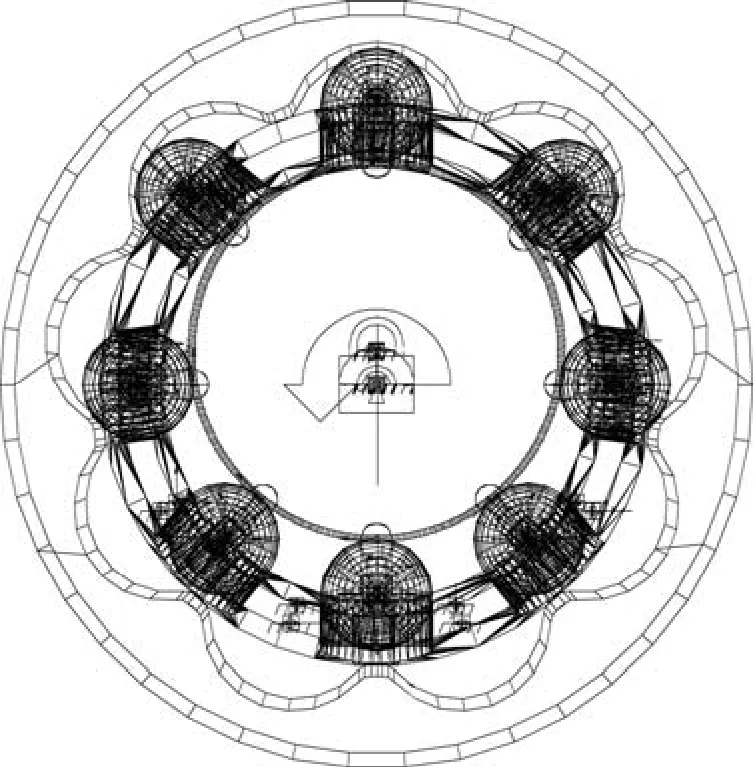
图5 谐波齿轮ADAMS模型透视图

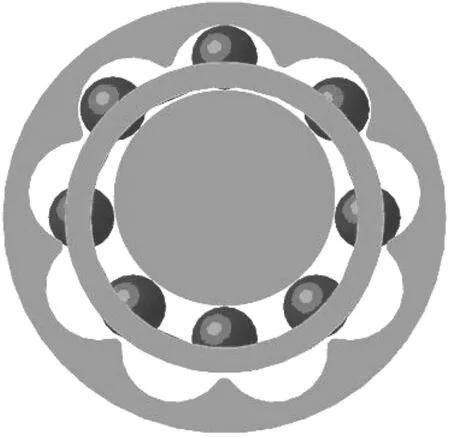
图6 谐波齿轮ADAMS模型实体图

3 仿真结果分析

ADAMS仿真模型中波发生器采用两种驱动输入：常值转速和正弦转速。通过对仿真数据结果的分析能够得到滚珠活齿谐波齿轮传动的一些特性，如图7～图10所示。

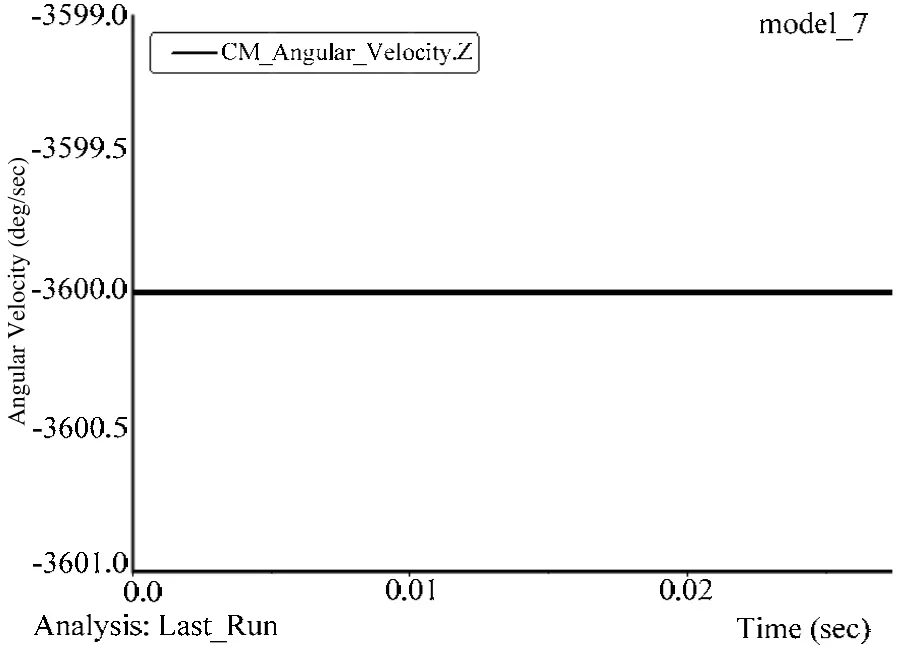
图7 常值转速输入(°/s)

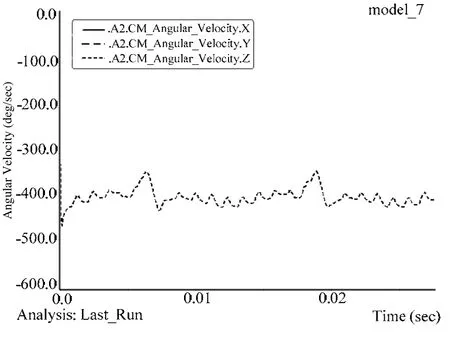
图8 常值转速输出(°/s)

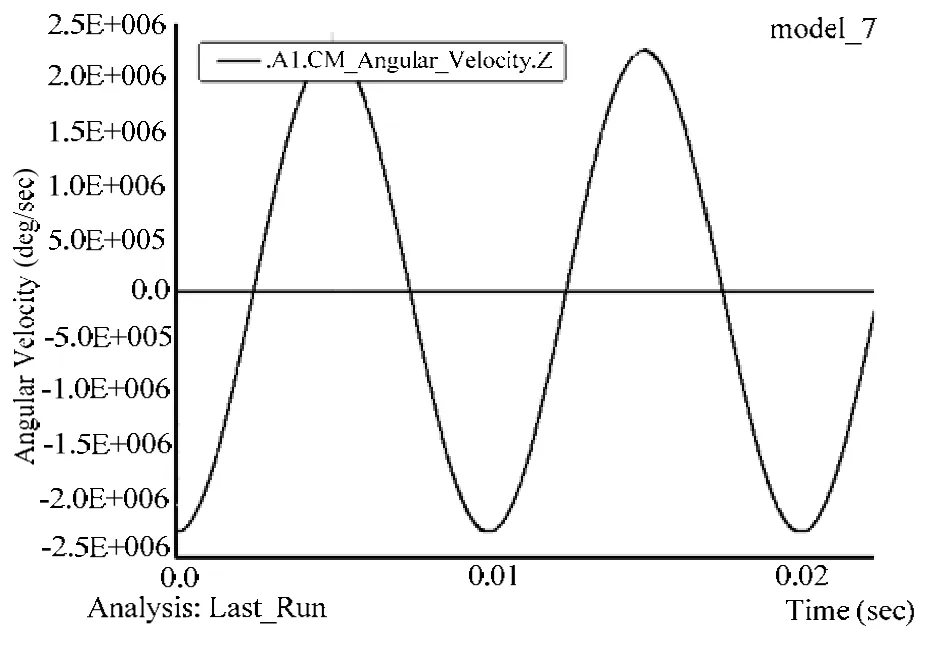
图9 正弦转速输入(°/s)

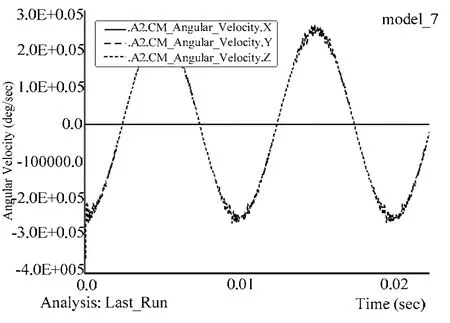
图10 正弦转速输出(°/s)

从仿真结果图中可以看出，无论是常值转速输入还是正弦转速输入，谐波齿轮都能较好地传递运动，减速比大约为9，与本文第二节中的优化结果符合。由于ADAMS造型工具简单，运动传递时还是存在抖动，而且输入转速低时抖动较大。

4 结 论

谐波传动作为自上世纪中叶发展起来的新兴传动技术，已经获得广泛应用，对其传动特性的研究还处在初级阶段。本文以受到研究关注较少但应用广泛的滚珠活齿谐波齿轮为例，推导得到了滚珠啮合及运动平稳传递的条件，并通过数值优化确定了若干关键参数。在此几何模型的基础上，建立了ADAMS实体仿真模型，仿真结果能够较好地反映谐波齿轮传动特性，并符合建立几何模型过程中的一些结论。后续研究将通过专业软件建立精确实体模型，导入到ADAMS中进行仿真，进一步讨论谐波齿轮的动力传递特性。

[1]李 峰. 活齿端面谐波齿轮啮合原理的研究[D]. 武汉: 武汉理工大学, 2004.

[2]宋立博, 吕恬生, 范元勋, 等. 谐波齿轮局部啮合屏幕仿真[J]. 机械科学与技术, 2000, 19(4): 566-567.

[3]辛洪兵, 秦宇辉. 谐波齿轮传动系统非线性扭转振动仿真软件设计[J]. 机械传动, 2005, 29(5): 32-36.

[4]王成刚, 张佑林, 姚传志. 活齿端面谐波齿轮减速器虚拟样机的运动仿真[J]. 工程图学学报, 2008,29(3): 7-22.

[5]郑建荣. ADAMS虚拟样机技术入门与提高[M]. 北京: 机械工业出版社, 2002: 2-3.