夹具平面定位误差计算软件的研制

康红杰，吴玉光

（杭州电子科技大学 机械工程学院，杭州 310018）

0 引言

由于夹具结构复杂且千变万化，人们提出了许多定位误差的计算方法，常用的方法包括利用尺寸链模型的极值法[1]和微分分析方法[2]、利用接触运动学模型的矩阵计算方法[3～7]、利用几何关系的图形解析法[8]和合成法以及概率计算方法[9]等。采用这些计算模型虽能求解定位误差，但是各种计算模型都是针对典型零件和特定夹具结构,缺少通用性，而且分析计算过程繁琐，难以实现自动化计算。

平面定位误差计算只考虑夹具的静态误差，即假定工件—夹具系统为刚体系统且不考虑机床和刀具的误差影响。在这一假设下，加工表面相对于夹具系统的位置是固定的，工件—夹具系统中与定位误差有关的要素有定位元件、定位基准、工序基准和加工表面四种。由于误差的存在，一批工件中每个零件的工序基准相对于夹具的位置是变动的，因此，可根据误差要素之间的位置关系，建立工序基准在夹具坐标系中的位置变化范围计算方法，从而求得加工表面相对于工序基准的位置变化范围，即定位误差。

本文根据夹具平面定位误差的表示方法[10]，采用基于微分分析的极值法计算原理，提出了夹具平面定位误差的分步计算方法，并编制了原型软件。该软件包括了平面定位情况下各种定位方式的定位误差计算，为夹具设计工程师提供了简便、精确地计算各种平面定位方式下的定位误差的计算工具。

1 定位基准相对于夹具的位置变动关系

1.1 定位元件与定位基准的位置变动关系

平面定位就是主定位基准限制工件的三个自由度之后，根据不同的定位要求，再对工件的2-3个侧定位基准进行定位，限制工件的其余3个自由度。典型的平面定位模式是3-2-1定位，即工件的两个互不平行的定位侧面分别用2个和1个定位元件与其接触，限制工件的两个平移自由度和一个转动自由度。侧定位面更一般的组成形式为3个不全平行的定位表面，每一个侧定位面分别用一个定位元件进行定位，即3-1-1-1定位[10]。由于平面定位误差的计算平面平行于主定位基准，因此分析平面定位误差时，侧定位面可以简化为其在计算平面上的投影。常见定位元件包括球头面、圆柱销、狭长平面、V形块等，其中狭长平面与平面定位基准接触可以等效于狭长平面的两个端点与直线基准接触，因此，分析平面定位误差时定位元件的几何类型可以简化为圆弧、直线和点三种。该思路同样可以扩展到复杂曲面定位情况。

图1、图2分别为文献[10]中总结的3-2-1、3-1-1-1定位模式下定位基准和定位元件的各种组合情况。在静态误差考虑范畴内，工件和定位元件的接触形式为点接触，对于给定的工件定位基准，除了一面两孔定位方式以外，其他定位方式下工件相对于夹具的公称位置都是确定的。因此，对这些定位方式可分别建立定位基准在夹具坐标系中的位置计算公式，再对位置计算公式分别关于各个误差要素变量进行全微分，就可以建立工件定位基准在夹具坐标系中的位置变动范围计算公式。这些误差要素包括了夹具装配图上的全部误差和公差元素，如定位元件位置坐标、元件尺寸、工件各定位基准位置公差、尺寸公差等，因此，定位基准位置变动范围计算公式包含了夹具装配图上的全部几何信息。

图1 3-2-1模式的全部定位情况

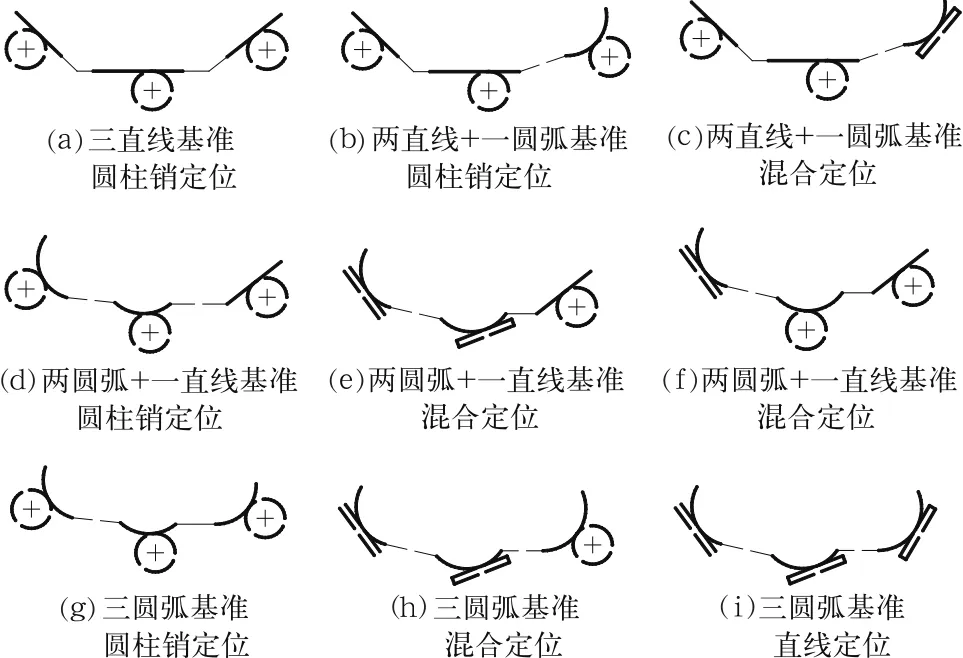
图2 3-1-1-1模式的全部定位情况

1.2 一面两孔定位方式的定位基准位置变动计算

一面两孔定位是最常见的平面定位方式，定位元件有两种组合方式，一种是两孔均用圆柱销定位；另一种是圆柱销和菱形销组合定位。两圆柱销定位时如图3（a）所示。由于销孔半径公差不同，两者之间存在间隙，销孔之间的接触点可能在圆周的任意位置上，使得工件两孔的中心连线相对于夹具的位置难以确定。可以认为孔中心的运动轨迹是以销的中心为圆心以孔销的半径差为半径的圆。因此对于双圆柱销定位情况可以认为工件相对于夹具做四杆机构运动，如图3（b）所示。根据杆长条件可具体判断四杆机构类型以及运动范围。

图3 双圆柱销定位情况

圆柱销和菱形销组合定位的定位方式见图4所示，菱形销通过弧ab、cd来限制孔中心的上下移动，而不限制工件定位孔中心的左右移动，即菱形销只限制工件y方向的移动自由度。图4（b）为菱形销上部圆弧面与定位孔接触和定位孔中心运动轨迹的放大图。当工件孔和菱形销自由配合，孔和弧ab接触时，孔中心的运动轨迹将是以O2为圆心，以(r4-r2)为半径的的一段圆弧。如果该圆弧的弓高远小于弦长，则鉴于该圆弧本身是一个微小量，可以认为孔中心的轨迹近似于直线。此外，实际定位时孔中心位置还受到另一个由圆柱销定位的孔的影响，使得孔与菱形销接触并不是纯滚动，但中心的位置必定在圆弧ef组成的弓内。因此，可以认为圆柱销和菱形销组合定位时，工件相对于夹具的运动近似于曲柄滑块运动。

根据图4可知，孔中心沿x轴方向的移动范围（DX）与z轴方向的移动范围(DZ)之比为：

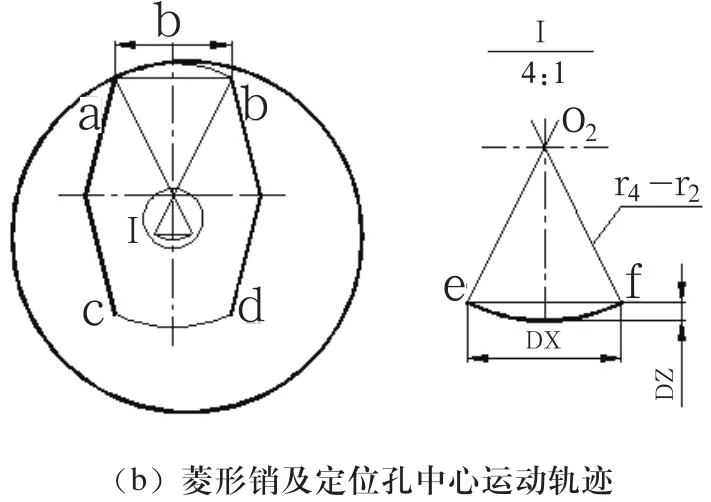
图4 圆柱销-菱形销组合定位情况

显然，该比值随2r2/b的增大而增大。表1列出了国家标准[11]中各种尺寸的菱形销所对应的宽度b的数值和相应的DX/DZ的比值。

表1 各种尺寸的菱形销的定位孔中心位置直线性

由表1看出孔中心所在的弧ef的弓高弦长比最小为5.2，最大22.3，且多数情况超过10倍，因此该弧的高度值与宽度值相比很小，可近似认为定位孔中心的运动为直线ef。由于圆柱定位孔与菱形销的上圆弧和下圆弧两种可能的接触情况，圆柱销和菱形销组合定位的曲柄滑块机构存在两种装配形式，如图5所示，其中孔中心偏离导轨的距离L4可由式（2）求得：

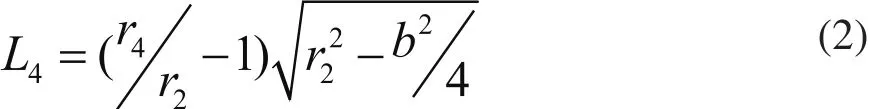
图5 圆柱销-菱形销定位的低副机构

2 工序基准相对于夹具的位置变动关系

夹具装配图上工序基准与定位基准之间有位置和公差标注，因此首先要建立工序基准相对于定位基准的位置变动关系，然后再将这一变动关系迭加到定位基准上，得到工序基准相对于夹具的位置变动关系。

虽然平面定位模式下工序基准和定位基准均有可能为圆或圆弧，但是圆弧基准的理论计算点为圆弧中心，故工序基准和定位基准之间的位置关系只要考虑点和直线之间的相对位置关系即可。当工序基准的几何类型为点时，相应的定位基准的几何类型为点和直线两种，这种情况下零件工序图上工序基准相对于定位基准的公差只有尺寸公差和位置度公差，此时工序基准相对于定位基准的位置及其变化只需一个距离关系即可描述完整。而当工序基准的几何类型为直线时，相应的定位基准的几何类型只能是直线一种类型，此时机械图上直线工序基准相对于定位基准的公差包括距离公差、角度公差、定形公差和定向公差。为了建立工序基准和定位基准的位置关系，必须将形位公差换算成距离公差和角度公差。以下介绍工序基准和定位基准均为直线的位置关系的建立方法。

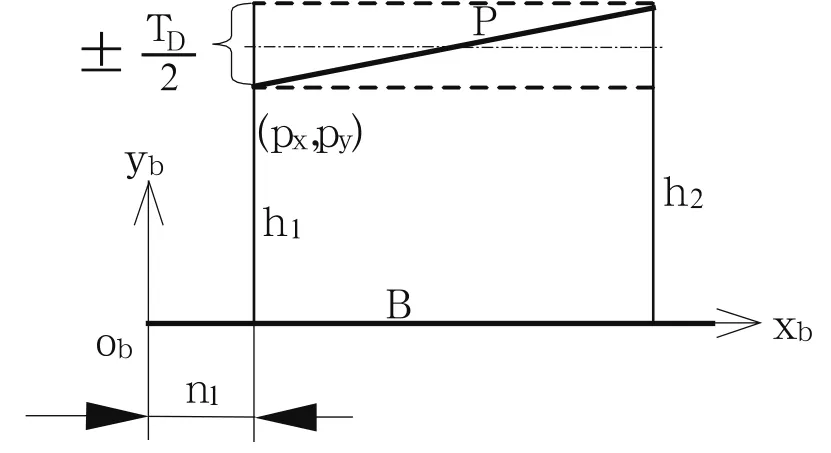
图6 工序基准相对于定位基准的误差计算模型

图6为工序基准与定位基准公称位置平行的情况，图中两条虚线表示工序基准的位置公差带TD，各种类型的公差数值均可以转化为公差带宽度，说明工序基准两个端点到定位基准之间的距离h1和h2的变化量为-TD/2 ～ TD/2，工序基准相对于定位基准的位置可以用n1、h1、h2三个参数表示。工序基准位置变动和定位基准位置变动的迭加只需乘以一个坐标变换矩阵即可。

3 加工表面与工序基准的位置关系

夹具定位误差是加工表面相对于工序基准在工序尺寸方向的位置变动量，在夹具静态误差的计算中，加工表面相对于夹具坐标系的位置是固定的，而工序基准相对于夹具的位置则要用一个变动范围加以表示，因此计算定位误差必须通过反算加工表面相对于工序基准的位置变动范围得到。

在平面定位中，加工表面的计算几何类型有直线和点两种类型，直线表示加工部位是平面或者圆柱面的中心线，点表示加工面为垂直于主定位面的圆柱或孔的中心点。由于工序基准的几何类型也有点和直线两种类型，因此加工表面和工序基准之间的工序尺寸类型就有点与点的距离、点到直线的距离，两直线之间的距离和倾角三种。这些距离和倾角的变化范围正是夹具的定位误差。

图7为加工表面和工序基准的几何类型均为直线时两者之间位置关系，加工表面M在夹具坐标系Ofxfyf中的位置是固定的，而工序基准P的位置则由图中的双点划线界定。因此需要根据工序基准的变化范围计算加工表面的两个端点到工序基准的距离d1、d2的变化范围确定加工表面相对于工序基准的位置变动范围，再根据d1、d2的变化范围换算出加工表面相对于工序基准的各项几何误差。

图7 加工表面相对于工序基准的位置

4 软件原型及实例介绍

4.1 软件开发平台

本软件以Pro/E为开发平台，采用Pro/TOOLKIT开发工具以及MFC可视化界面技术。Pro/TOOLKIT是Pro/E自带的功能强大的二次开发工具，它提供了开发Pro/E所需的函数库文件和头文件，使用户编写的应用程序能够安全地控制和访问Pro/E，并实现应用程序模块与Pro/E系统的无缝集成。

定位误差计算全过程包括：1）将夹具装配图上全部公差转化成对称形式；2）求解定位误差；3）将定位误差转化成工程图中要求的表示形式。软件的输入为二维夹具和工件装配图，用户在使用软件时，首先通过人机交互选择定位方式，程序调用相应的子程序，提示用户拾取定位元件和定位基准、程序自动获取定位元件和定位基准工程位置信息，用户从对话框中输入夹具元件和定位基准的位置和形状公差参数，程序将计算结果输出到对话框中。第二步再以相同的过程调用工序基准计算模块，第三步调用定位基准反算模块计算定位误差。第二步和第三步可以反复调用，直到本次装夹加工中全部加工表面的全部定位误差计算完成。图8为定位基准位置变动计算模块的交互界面。

4.2 实例介绍

图9中所示零件铣削台阶面A的侧面对盲槽B的中心线有平行度要求，由于生产工艺要求，盲槽B已在前道工序中加工完成。本道工序加工工件采用一面两孔定位，定位方案及工序尺寸如图10所示，本道工序属于工序基准与定位基准不重合情况，定位误差就是计算台阶侧面两端点到盲槽中心线的延长线上的距离尺寸的变化情况。

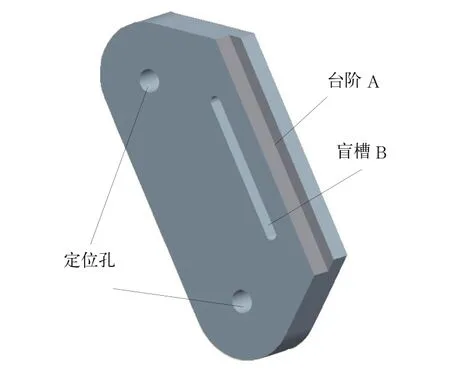
图9 实例零件

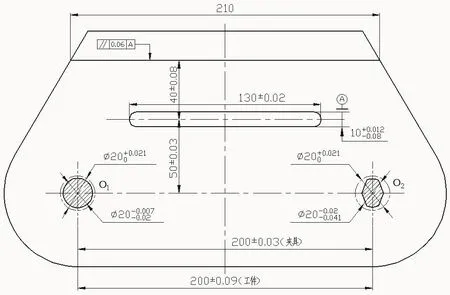
图10 工序简图

在Pro/E中启动定位误差计算软件，首先从下拉式菜单中选取“选择定位方式”项，弹出定位方式选择对话框（如图8所示），选择一面两孔定位对应类型14，然后程序弹出图11所示对话框，提示用户通过人机交互从屏幕上拾取圆柱定位销和菱形定位销，程序自动获取直径、位置和距离等公称数据，并填写到相应的编辑框中，对于公差值数据目前还需根据根据工序简图再经过换算之后手工填写。

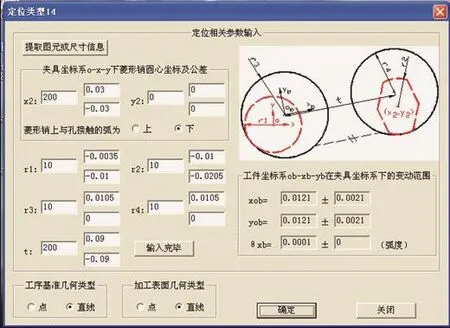
图11 定位基准参数输入定话框

各参数的含义均在对话框右侧的提示图中标出，其中夹具坐标系o-x-y建在圆柱销圆心上，工件坐标系ob-xb-yb建在圆柱销定位的孔心上，xb轴在两孔的连心线上。图10中标出菱形销和圆柱销圆心距离在水平方向有±0.03mm的公差，故在填写对话框时菱形销中心坐标x2有±0.03mm的公差。本例中由于菱形销位于夹具坐标系的x轴上，故菱形销中心坐标y2没有公差。根据零件的结构，应使夹具的夹紧力方向向上，即选择菱形销下圆弧与孔接触。该零件的工序基准和加工表面的几何类型均为直线，并且工序基准与定位基准不重合。图11的对话框完成了零件定位基准和夹具元件的参数输入，计算出工件定位基准相对于夹具的位置变动范围并显示在对话框上。

图12是工序基准相对于夹具坐标系的位置变动计算对话框，要求输入工序基准相对于定位基准的参数数据、加工表面特征相对于工序基准的位置参数和位置关系信息。

图12 工序基准参数输入对话框

本例工件的工序基准为盲槽中心线，加工表面为台阶侧面投影线。根据顺序选择盲槽中心线和台阶侧面投影线，程序自动计算出台阶侧面投影线端点在盲槽中心线延长线上的对应两个投影点坐标，并自动填写到相应的对话框中。由于本实例零件是计算台阶侧面投影线两端点到盲槽中心线的距离变化范围，不需要工序基准两端点的x坐标的公差信息，故将x坐标的公差值填0。除了人机交互选择工序基准和加工表面之外，也可以直接在编辑框中输入和修改具体的坐标以及公差值。以使计算更准确，然后填写台阶侧面两端点在夹具坐标系下的坐标值。至此，输入部分结束。选择确定按钮，弹出计算结果对话框显示，如图13所示，输出台阶侧面两端点到工序基准延长线的距离和公差。

图13 计算结果对话框

以尺寸链方法手工解出d1、d2公差分别为±0.051mm和±0.061mm，因此可以认为本软件计算结果正确。

5 结论

将工件—夹具系统中与定位误差有关的要素归纳为定位元件、定位基准、工序基准和加工表面四种，从而提出一种适用于人机交互的定位误差分步计算方法。该方法完全包含了夹具与工件系统的工艺信息，便于软件模块化设计、符合工程实际求解过程思路，方便利用软件实现交互计算。

下一步研究基于三维夹具装配模型的参数信息自动获取方法，以提高软件的自动化程度。

[1] 杨一帆,庄仲禹.应用尺寸链原理计算夹具定位误差[J].机械研究与应用,1994(4):16-19.

[2] 马成习,微分法在定位误差计算中的应用[J].工艺与检测,2008(4):130-132.

[3] WU Y,Rong Y,Ma W,et al.,Automated modular fixture planning:geometric analysis[J].Robotics&Computer-Integrated Manufacturing,1998,(14):1-15.

[4] WU Y,Rong Y,Ma W,et al.,Automated modular fixture planning:accuracy,clamping,and accessibility analysis.[J]Robotics&Computer-Integrated Manufacturing,1998,(14):16-26.

[5] 秦国华,张卫红.基于运动学方法的线性尺寸定位误差通用建模与分析[J].机械科学与技术,2004,23(11):1317-1320.

[6] 秦国华,吴竹溪,张卫红.夹具定位方案的数学建模及其优化设计[J].中国机械工程,2006,17(23):2425-2429.

[7] TSAI Y H,LU S S,Localization accuracy matrix analysis for localization accuracy consideration in 2D precision fixture system[C],2007 Mediterranean conference on control and automation,July 27-29,2007,Athens,Greece.

[8] 刘让贤,郭紫贵,凡进军.基于图形法的机床夹具定位误差计算[J].装备制造技术,2007(5):34-35.

[9] 郭春生,张树人.夹具定位误差分析的概率法[J].长春光学精密机械学院学报,1985(2):81-86.

[10]吴玉光,宋建青.夹具平面定位误差的连杆机构模型及其概率分析[J].计算机集成制造系统,2010,16(12):2596-2602.

[11]杨黎明.机床夹具设计手册[M].国防工业出版社,1996:434-435.