降雨作用下山区边坡稳定性分析

李德心，何思明，李军歌，朱兴华，黄江成

（1.中国科学院 水利部成都山地灾害与环境研究所，四川 成都 610041；2.中国科学院研究生院，北京 100039；3.四川省交通厅交通勘察设计研究院，四川 成都 610017）

0 引言

降雨诱发的边坡破坏，尤其在我国降雨比较丰富的西南山区灾害中占很大的比重，因此，开展降雨对山区边坡稳定性影响研究，可以为边坡滑动的监测预警和预测预报提供技术支撑，对工程安全、环境保护和减灾防灾也具有重要理论意义和工程意义。

从目前国内外的研究现状看：在降雨条件下，滑坡的临界启动条件，主要通过现场调查，测绘以及GIS技术对滑坡相关参数进行收集整理、采用数理统计，回归方法建立滑坡发生和降水临界值之间的经验公式，此方法简单、便于应用，但缺乏物理基础。事实上，不同流域、不同性质的滑坡临界启动条件是不同的。

Montgomery ＆ Dietrich（1994）［1］将坡地水文模型与无限边坡稳定模型相结合，给出了浅层滑坡启动的临界降雨强度计算公式，结合GIS技术研究了降雨诱发滑坡的危害区域；兰恒星、周成虎、王苓涓等（2003）［2］有效地将地表地形与斜坡的地下水运动特征结合起来，进行滑坡的稳定性分析，将工程中广泛采用的极限平衡方法与基于DEM的水文分布模型进行有效的集成，提出滑坡-水文耦合模型。此外，Kang-Tsung Chang（2009）［3］、Casadeietal（2003）［4］等也对此进行了研究，取得了较好的效果。

本文在总结国内外学者在降雨对边坡稳定性研究成果的基础上，将上述研究方法引入到降雨对山区边坡稳定性影响研究，构建模型进行分析，提出研究中存在的问题和相关建议。

1 降雨边坡水文模型

滑坡的发生通常受降雨的影响（图1），渗流过程导致边坡土体含水量的变化，上游集水盆地中充沛的水源浸润斜坡土体，降低浅层斜坡土体的稳定性，最终导致滑坡的发生。滑坡土体的厚度为Z，由达西定律知降雨作用下通过某断面的流量Q为：

式中：v——渗流速度（m/s），v=ki其中k为渗透系数（cm/s），i=sinα为水力坡度，α为边坡体倾角（°）；

F——过水断面（m2），可表达为：

式中：b——集水道宽度（m）；

h——滑坡土体中地下水的水层厚度（m）。

结合上述（1）、（2）式有：

特别是随着降雨量的增加，滑坡土体中潜水位不断上升，当h=z时，堆积体充满水并达到完全饱和状态，根据I与单元坡上集水区面积A的乘积为流径宽度b的单元的地下迳流量：

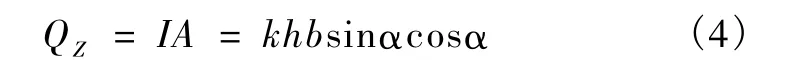
当滑坡土体处于全部饱和状态时，流径单元的迳流量等于导水系数T与水力梯度 sinα及斜坡宽度b的乘积［2］：

图1 边坡体水文模型Fig.1 Hydrological model of landslide

假定水力传导性在滑坡体的深度方向上均匀分布，即不随深度而产生显著的变化，则滑坡土体的导水系数T=kz，其它符号意义同前。

将（4）、（5）式两边相除，可推导出特定降雨强度下，滑坡土体中潜水厚度［2］：

式中：I——等效降雨强度；

A——滑坡体流域面积；

Z——滑体铅直厚度（m）；

T——饱和土体的渗透系数（m2/d）；

b——考虑的水流横切面宽度（m）；

α——滑动面倾角（°）。

2 降雨入渗边坡稳定性分析

在一些假设条件的前提下，从降雨诱发边坡失稳的机理，建立简化的粘塑性的滑体模型进行分析。

如图2所示，假定地下水位面 、滑动破裂面与地表平行。根据极限平衡原理，考虑静水压力及动水压力（渗透压力），可以建立以下模型：

式中：F——下滑力；

Fr——抗滑力；

m——滑体质量；

a——加速度；

则平行于斜坡方向上的动量平衡方程可以简化为：

式中：τ——抗剪强度；

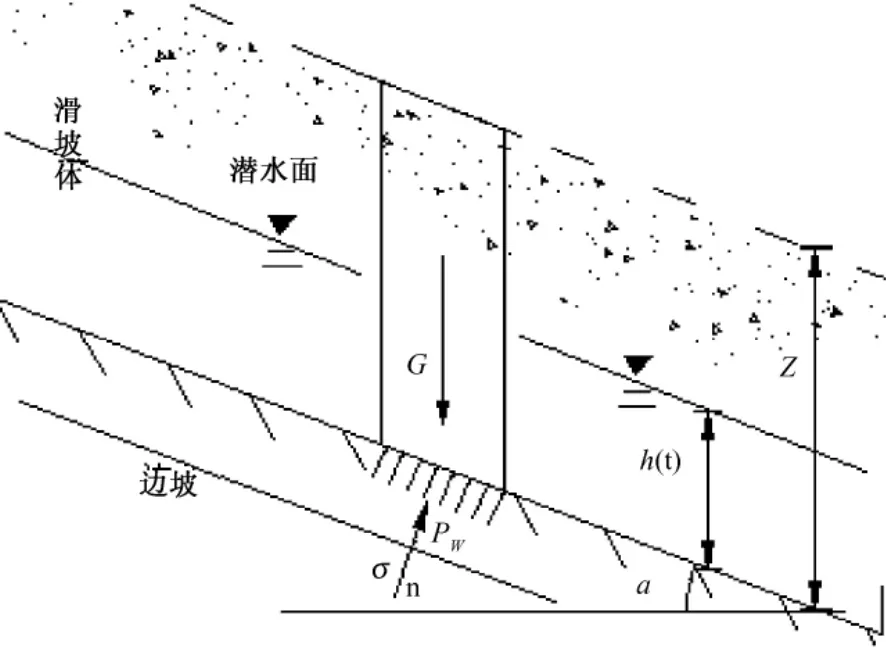
图2 边坡体滑动计算模型Fig.2 Computational model of landslide

c′——有效粘聚力（t/m2）；

σ——法向应力；

pw（t）——孔隙水压力（地下水对边坡体起的作用）；

φ′——有效内摩擦角（°）。

根据摩尔库伦定律化简如下：

式中：h（t）——滑坡体饱水部分铅直厚度（m）；

γw——水的重度（N/m3）；

α——滑动面倾角（°）；

根据极限平衡原理，滑坡体的稳定系数为：

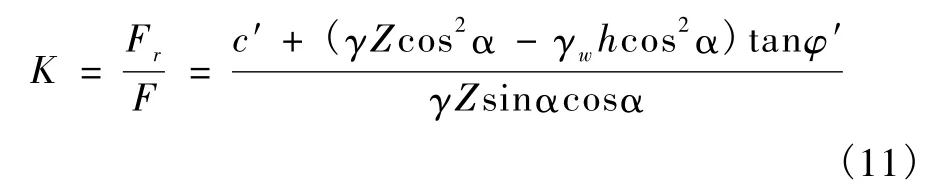
式中：K——稳定系数，当K=1时，滑坡开始启动，由此可以确定滑坡启动的临界条件。

根据坡地水文模型和无限边坡理论，结合（6）-（9）式，推导出降雨滑坡临界雨量的计算公式：

式中：Icr——临界降雨量；

T——饱和土体的渗透系数（m2/d）；

b——考虑的水流横切面宽度（m）；

A——滑坡体的汇水面积（m2）；

γ——滑坡体天然重度（N/m3）；

φ′——堆积体有效内摩擦角（°）；

c′——堆积体有效粘聚力（kPa）；

Z——滑体铅直厚度（m）。

根据太沙基一维固结原理：

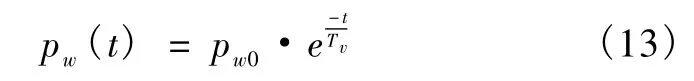
式中：pw（t）——孔隙水压力（kPa）；

pw0——初始孔隙水压力；

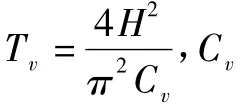
H——压缩土层的排水距离（cm）。

3 算例与分析

西部山区其地形、地貌和地质水文条件复杂，公路修建过程中常遇到各种各样的边坡问题。本文结合四川省都江堰某山体滑坡为例，对降雨条件下，滑坡的变形破坏进行分析。采用以下参数（表1）：

表1 降雨滑坡体计算参数Table 1 Parameters and material properties of Slope

3.1 边坡破坏的临界降雨条件

根据表1的数据，通过公式（13）式我们可以推算出降雨作用下的临界降雨量为：Icr=62.32mm/d，也就是说当该地的降雨量大于此临界降雨量时，就很容易发生山体滑坡。

3.2 影响边坡体滑动因素的敏感性分析

在滑坡土体性质完全确定的条件下，结合计算实例研究了不同的降雨量对边坡稳定性系数的影响、边坡倾角、内摩擦角和滑坡启动临界降雨量的关系，计算结果见图3～图5。

根据初始地下水位高度为1m，当降雨量分别为20mm/d、25mm/d、30mm/d、40mm/d、50mm/d 时，地下水位线高度分别上升为2.37m、2.72m、3.06m、3.75m、4.44m，其稳定系数分别为：1.316、1.266、1.218、1.119、1.019。

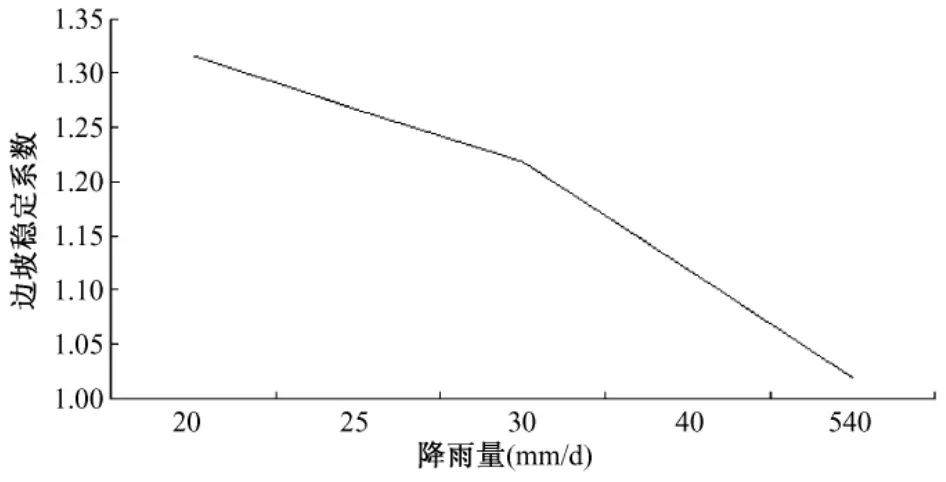
图3 降雨量与边坡稳定系数关系图Fig.3 The critical rain fall versus the safety factor

图3结果表明：在边坡倾角、土体内摩擦角一定的条件下，边坡稳定系数随着降雨量的增加呈线性关系减小。

当边坡倾角为分别是 30°、32°、35°、38°时，滑坡启动的临界降雨量分别为62.32mm/d、54.83mm/d、40.73mm/d、22.41mm/d。

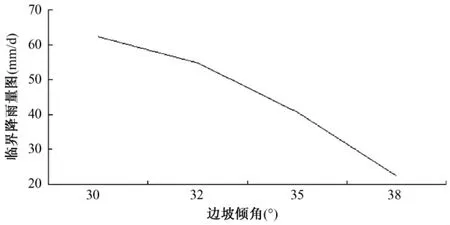
图4 边坡倾角与滑坡启动临界降雨量关系图Fig.4 The critical rainfall versus the slope angle

图4给出了滑坡启动的地下水位高度与边坡倾角的关系，从图中可以看出：滑坡启动的临界降雨量均随边坡比降的增加而减少，也就是说斜坡坡度越陡，越容易导致滑坡的发生。

当土体内摩擦角分别为 30°、33°、36°、40°时，滑坡启动的临界降雨量分别为34.87mm/d、49.60mm/d、62.26mm/d、76.36mm/d。

图5给出了滑坡启动的临界降雨量与斜坡土体内摩擦角的关系，从图中可以看出：不同的土体内摩擦角，滑坡启动的临界降雨量均随边坡土体内摩擦角增加而增大。

图5 内摩擦角与滑坡启动临界降雨量关系图Fig.5 The critical rain fall versus internal friction angle

4 结论

本文是在总结前人研究的基础上，建立最简单的动力学模型，在一定的降雨激发条件下，可能导致滑坡的启动。以坡地水文模型为基础，结合无限边坡稳定计算模型，研究了边坡在降雨激发条件下的临界启动条件，给出了控制滑坡启动的临界控制方程，并结合西部山区某滑坡，研究了降雨强度、边坡坡度、内摩擦角对滑坡启动的影响，并得出了如下结论：降雨量与边坡体稳定系数成反比；随边坡坡度的增大而减少；随着边坡土体内摩擦角的增加逐渐增加。相关研究成果可以为山区降雨型边坡滑坡的预测预报提供技术支持。

［1］Montgomery，D.R.，Dietrich，W.E..A physically based model for topographic control on shallow landsliding［J］.Water Resources Research ，1999，30：1153-1171.

［2］兰恒星，周成虎，王苓涓，等.地理信息系统支持下的滑坡—水文模型研究［J］.岩石力学与工程学报，2003，22（8）：1309-1314.LAN Hengxing，ZHOU Chenghu，WangLingjuan，et al.GIS based landslide stability and hydro-logical distribution coupled model［J］.Chinese Journal of Rock Mechanics and Engineering，2003，22（8）：1309-1314.

［3］Kang-Tsung Chang，Shou-Hao Chiang.An integrated model for predicting rainfall-induced landslides［J］.Geomorphology，2009，105：366-373.

［4］CasadeiM，Dietrich，W E，et al.Testing a model for predicting the timing and location of shallow landslide initiation in soil-mantled landscapes［J］.Earth Surface Processes and Land form，2003，28：925-950.

［5 ］Iverson R M.Landslide triggering by rain infiltration［J］.Water Resources Research，2000，36：189-191.

［6］Matthias Jakob，Hamish Weatherly.A hydroclimatic threshold for landslide initiation on the North Shore Mountains of Vancouver，British Columbia ［J］.Geomorphology，2003，54：137-15.

［7］C L SHIEH，Y S CHEN，Y J TSAI，et al.Variability in rainfall threshold for debris flow after the Chi-Chi earthquake in central Taiwan，China［J］.International Journal of Sediment Research，2009，24（2）：177-188.