高空台加温试验进气管网传热过程的计算分析

朱剑鋆，董葳，吴锋，田小江

(1.上海交通大学机械与动力工程学院，上海200240；2.中国燃气涡轮研究院，四川江油621703)

高空台加温试验进气管网传热过程的计算分析

朱剑鋆1，董葳1，吴锋2，田小江2

(1.上海交通大学机械与动力工程学院，上海200240；2.中国燃气涡轮研究院，四川江油621703)

分析了高空台加温试验时管网内部流动的动态换热特性，建立了管内气体和管壁的联合换热方程，在与试验数据对比的基础上提出了数学模型的修正方法，对试验中管网出口温升过程进行了计算，取得了较好效果。计算结果分析表明：局部热损失在管网散热过程中的比重较大，为缩短试验准备时间，应对混和器出口温度进行分段控制。

高空台；瞬态传热；数值模拟；管网

1 引言

航空发动机高空模拟试验是现代航空发动机研制过程中必不可少的试验手段，而高空模拟试验的右包线模拟范围或部分试验科目均要求有较高的发动机进口模拟温度，因此需要对进气进行加温[1～3]。然而，由于供气管网在热气输送过程中存在较大的热损失[4]，在现有试验中必须花费大量的时间使流入试验段的气体温度达到试验要求，这样就会延长整个试验的周期，增加试验成本。

若能获得较为准确的管网出口温升响应关系，就能有效指导高空台试验中控制参数的设置，从而提高试验效率。近年来，计算流体力学和传热学不断完善，在试验模拟中已得到较为广泛的应用[5，6]，且在管网优化和流动分析中也发挥了一定作用[7，8]，这就为采用计算手段预测管网出口温升过程奠定了基础。

目前，国内对高空台供气流程的计算研究主要集中在控制系统和过程仿真[9，10]，还没有出现与管内流固换热相关的报道。本文对高空台管网系统中气体和固体间的换热过程进行了分析，建立了相应的一维非稳态管网换热计算模型，并在此基础上对流入试验段的气体温度进行了计算，得到了较为理想的结果；同时以试验数据为基础，提出了计算曲线的修正方法。

2 总体计算过程和基本假设

本文计算的管网系统结构如图1所示。热空气从1#管道流入，在2#、3#管道入口处分流，随后在出口处与由阀1进入的外部大气掺混，依次通过4#和5#管道并流入试验段。

图1 计算管网的结构示意Fig.1 Pipe network structure in calculation

在热气流动过程中，其热量损失可分为局部损失和沿程损失。其中局部损失由管网接口、阀门以及气流掺混等因素引起，用现有理论还无法进行准确分析；沿程损失可根据流体力学及传热学的基本理论求解。由于局部热损失不会对整体的温升趋势造成影响，因此本文在计算时先对不计局部热损失的每根单管进行考虑，然后再根据计算结果和相关试验数据，确定管网局部热损失的修正方法。

考虑到圆管的对称性以及管内气体温度的分布规律，本文在计算管内空气温度时只考虑了沿流动方向的热量传递。同时，由于管壁在径向的热交换远大于其沿流动方向的热交换，因此可将管壁的能量传递简化为沿径向的一维导热。为使计算顺利实施，本文还作了如下几点假设：

(1)管径较大，管内流速相对较低，故空气按照不可压缩流体处理；

(2)由于气体在混合器中进行了充分掺混，故认为混合气出口气体为完全湍流；

(3)管壁及其外部包覆的绝热材料间密实接触，各材料层厚度均匀；

(4)环境温度保持不变。

3 基本计算方程

3.1 单独管段气体的计算方程

高空台供气管网各单独管段的结构如图2所示。图中w0为钢质管壁，w1和w2为由玻纤、发泡材料制成的两层保温层，r0至r4为各材料壁面到管道中轴的距离。

取图2中长为dx的空气微元作为控制体，其应满足连续性方程[11]：

图2 管内流动气体的控制体Fig.2 Control volume of the air in pipes

动量方程：

能量方程：

以及理想气体状态方程：

由于管路长度相对管径较小，可近似认为管内压力不变，又因为空气按照不可压缩流体处理，因此可不必求解动量方程，连续性方程可简化为：

以上各式中：下标air表示空气，w表示壁面，in表示管道内壁面位置，x表示管内任意位置，inlet表示入口位置。

3.2 多层管壁的计算方程

管壁为三层结构，由于各层材料间密实接触，故层与层之间只存在导热的换热方式。结合壁厚均匀的假设，可得到管壁的导热微分方程：

式中：i代表壁面所在的层。在壁面交界处，满足热流连续条件：

各层材料的热学性能采用如表1所示的参考值[12～14]。

表1 管壁材料的热学性能Table 1 Thermal performance of the pipe wall material

3.3 对流换热关系式

(1)内壁面与空气的对流换热系数

管内空气与内壁面的换热采用湍流管内强制对流换热关系式计算。由于管径较大，管内换热的入口段效应不能忽略，此处采用Gnielinski公式计算：

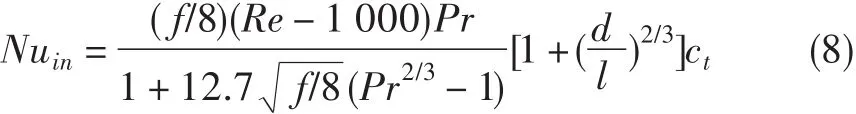
(2)外壁面与环境的对流换热

由于管网段处于非密闭环境中，可采用大空间自然对流换热关系式计算外壁面与环境的对流换热量：

式中：下标out表示管道外壁面位置。

3.4 等效热损失

等效热损失是计算过程中引入的修正量，目的是体现建模时忽略的管网局部热损。由于换热量与温差呈正比，因此必须给定一个参考温差。本文采用稳定供气时的入口平均温度与环境温度的差作为参考温差。等效热损失应为未加修正时，对某次基准试验计算得到的温升曲线与试验曲线在同一时刻所反映出的焓差，将单位流量的焓差除以参考温差便可得到等效热损失系数。在进行试验温升预测时，只需将该系数与流量及入口与环境温度之差相乘即可得到修正的热损值。

4 计算方程的数值求解方法

4.1 方程的离散

(1)管内气体的能量方程

管内气体的换热以对流为主，因此采用有限差分的迎风格式对该方程进行离散。网格节点标号如图3所示。考虑到解的稳定性，在离散中采用隐格式：

式中：下标n的相关项表示计算微元的位置节点，上标j的相关项表示计算微元的时间节点。

(2)多层管壁的导热方程

由于原始微分方程不包含不同材料交界处的信息，所以此处采用热平衡法给出离散后的壁面导热方程，离散采用中心差分隐格式。壁面网格节点如图4所示，取两节点中间处的面积作为导热面积。

图3 管内空气的计算节点Fig.3 Grids of air in pipes

图4 管壁导热的计算节点Fig.4 Grids of solid walls

①相同材料内部的导热方程

根据热流量平衡，有：

②材料交界节点处的导热方程

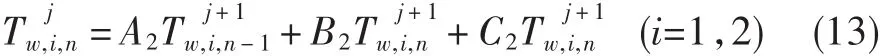
③内外边界的导热方程

对内壁面，有：

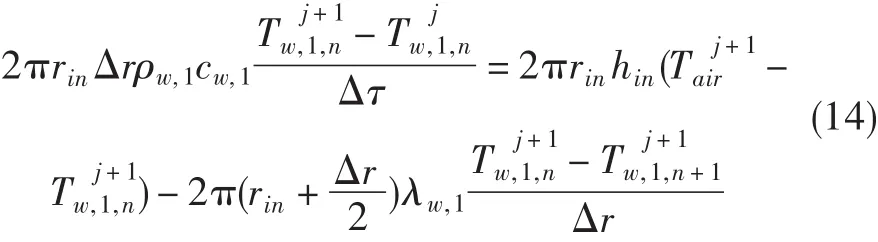
对外壁面，有：

式中：下标env表示环境。

4.2 模型求解

(1)初始条件和边界条件设定

为求解上述方程，给出合适的初始条件和边界条件十分必要。求解所需边界条件包括管道入口处的压力、温度、流量随时间的分布；初始条件主要有管内气体的温度分布和管壁的温度分布。本计算中，管内初始温度和壁面初始温度均按环境温度处理，边界条件则根据试验数据给出。

(2)总体计算流程

本计算针对管网系统流动换热耦合问题，主要关注点在于前室出口气流温度随时间的变化。由于管内气体温度与管壁温度始终相互影响，因此在两者的传热计算中采用相同的时间步长。

由于给定了初始气流温度分布和管壁温度分布，因此可根据式(11)得到下一时刻轴向各计算节点的温度分布。再结合式(12)～式(15)，就可得到各轴向节点位置的壁面径向温度分布。重复这一计算过程直至达到所需计算时间，即可对前室出口温度进行动态预测。主体计算流程如图5所示。

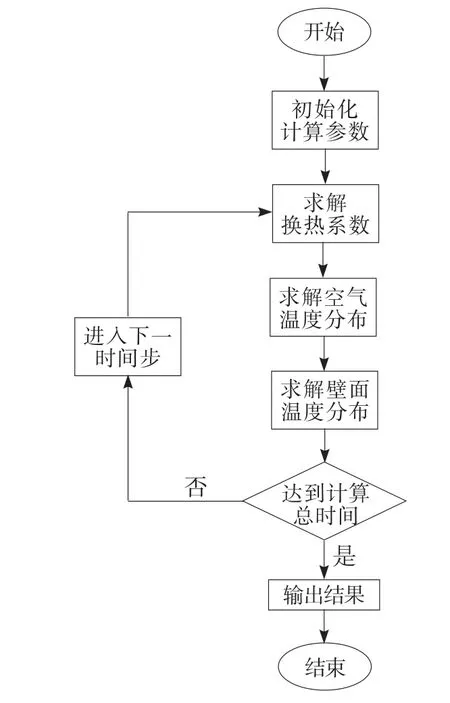
图5 计算流程Fig.5 Calculation scheme

5 算例计算及结果分析

为验证计算模型的合理性，本文对两个不同试验状态下的前室出口温度进行了动态模拟，并以第一组数据作为基准数据，得到了管网的等效热损失系数。相关试验参数如图6和图7所示。计算时，选取时间步长为1 s，径向空间步长0.1 m。根据实际试验情况，第一组数据的环境温度为27℃，第二组为24℃。

图8(a)为未考虑局部热损失情况下的前室出口温升曲线。从图中看，两曲线在趋势上一致，均呈现出明显的分区性，即在初始阶段管网出口温度以较快速度上升，到达某一时刻后温升速度急剧放缓，这表明管网出口温度在不同时间段内受不同因素的支配。在初始阶段，管网出口和入口截面存在较大的温差，热量主要通过气流流动进行传播，尽管热气在流动过程中存在热损失，但与出口截面相比管内气体的温度仍然较高，因此在这段时间内出口截面的温升较快。当温升过程持续一定时间后，前室出口截面温度与流至该截面的气流温度之差变小，同时管壁与热气的温差也相对减小，此时截面的温升主要是由于管内空气热量流失减小而引起，因此造成截面温度缓慢上升的现象。

从对比结果看，在缓慢温升阶段，数值结果与试验结果约相差一恒量，这即为管网的局部热损失量。这一现象表明了本文将局部热损失和沿程热损失进行分类考虑的合理性，同时也表明局部热损失在整个管网散热中占有较大的比重。为使计算结果更具可用性，采用本文提出的局部热损失修正方法对图8(a)中曲线进行修正，结果如图8(b)所示。从图8(b)中可以看到，修正后的曲线能较好地反映实际的温升过程；虽然初始温升阶段后期以及试验结束后管内温降的计算结果与试验结果有所出入，但这并不影响本文方法在试验温升时间预测中的运用。

图6 第一组试验数据Fig.6 Experimental results of group one

图7 第二组试验数据Fig.7 Experimental results of group two

图8 第一组试验中的前室温升过程Fig.8 Temperature raising process of group one

为验证修正系数的可移植性，采用第二组试验数据对温升过程进行计算，结果如图9所示。图中表明，基于基准试验数据得到的等效热损失系数对其它试验条件下的局部热损失估计同样有效。因此，采用该修正系数对试验温升过程进行预测所得结果可信。

图9 第二组试验数据的温升过程模拟Fig.9 Temperature raising process of group two

从图8(b)和图9中不难发现，要达到试验设定温度，往往需要耗费大量时间来对管内气体进行加热，且大多数加热时间都处于缓慢温升过程，这与目前试验中对管网入口温度的设定有关。从图6和图7中可以看到，两组试验中入口温度的设定基本上都维持在略高于试验所需温度水平(所需试验温度的1.1倍左右)，因此管网出口温度虽然在较短时间内就达到了所需试验温度的80%左右，但要达到所需试验温度仍须一漫长过程。根据计算结果，这一过程时间约为使空气温度达到80%试验温度所需时间的7～8倍。一种提高试验效率的可行方法是：在试验前用本文方法对不同供气温度的管网出口温升过程进行预测，找出较为合适的试验初始供气温度设定值以及试验时应维持的供气温度，这样即使预测情况与试验情况不完全吻合，但也只需在试验时进行细微调整，从而有效避免因供气温度选择不佳导致的试验时间和成本增加。

6 结论

(1)局部热损失在管网散热过程中占有较大比重，但对于管网出口温升趋势没有大的影响。

(2)前室出口温度上升在不同阶段受不同因素支配，初始阶段温升速度较快，随后大幅放缓。要使前室出口温度快速满足试验要求，应在初始阶段适当提高混合器出口温度，当前室出口温度快要达到所需温度时，再适度调低混合器出口温度，以使前室出口温度稳定维持在试验要求范围内。

[1]杜鹤龄.航空发动机高空模拟[M].北京：国防工业出版社，2002：1—31.

[2]张宝诚.航空发动机试验和测试技术[M].北京：北京航空航天大学出版社，2005：410—431.

[3]焦天佑，郭昕.高空台在发动机研制中的作用和发展设想[C]//.珠海航空学术会议航空动力论文集.1998：314—318.

[4]陆宝富.高空台空气加热炉试验与研究[J].燃气涡轮试验与研究，1995，8(2)：60—62.

[5]Barton J M.Role of Computational Fluid Dynamics in Aeropropulsion Ground Testing[J].Journal of Aircraft，1984，21(10)：745—750.方面，处理机匣能将这部分流体向风扇转子上游区域输运并射入主流，增加了转子的轴向动量，有效地抑制了间隙泄漏涡破裂现象的发生。

(4)径向倾角选为45°比选为60°的损失略小，且扩稳能力略强。本研究对类似单级跨声速风扇处理机匣设计具有一定的参考价值。

参考文献：

[1]Wilke I，Kau H P.A Numerical Investigation of the Flow Mechanisms in a HPC Front Stage with Axial Slots[R]. ASME GT2003-38481，2003.

[2]卢新根，楚武利，张燕峰.跨音速压气机间隙流与处理机匣相互作用分析[J].西安交通大学学报，2006，40 (11)：1357—1360.

[3]王永明，胡骏，屠宝锋，等.带处理机匣的跨声速风扇非定常数值模拟[J].南京航空航天大学学报，2006，38 (5)：540—544.

[4]祝剑虹，朴英，周建兴.跨声压气机缝式处理机匣非定常模拟研究[J].航空动力学报，2007，23(5)：882—888.

[5]Emmrich R，Kunte R，Hönen H，et al.Time Resolved In⁃vestigation of an Axial Compressor with Casing Treatment Part 2-Simulation[R].ASME GT2007-27582，2007.

[6]Fujii K.Progress and Future Prospects of CFD in Aero⁃space-Wind Tunnel and Beyond[J].Progress in Aerospace Sciences，2005，41(6)：455—470.

[7]Tony C，Mike M.Pipeline Optimization by Computer Simu⁃lation[C]//.The International Pipeline Conference.2000：1—5.

[8]Chang S Y.A Program Development for Unsteady Gas Flow Analysis in Complex Pipe Networks[C]//.The 33th PSIG Annual Meeting.2001：9—22.

[9]张松，郭迎清，赵涌，等.进排气调压系统半物理仿真程序的设计与实现[J].计算机测量与控制，2010，18 (2)：401—403.

[10]马前容，田金虎.数值仿真在发动机高空试验稳态性能评估中的应用研究[C]//.中国航空学会动力分会第七届发动机实验技术学术年会论文集.CSAA2005-PET-026，2005：170—175.

[11]White F M.Fluid Mechanics[M].5th ed.2004：227—244，601.

[12]杨世铭，陶文铨.传热学[M].4版.北京：高等教育出版社，2006.

[13]皮茨D，西索姆L.传热学[M].2版.葛新石，叶宏，陈则韶，译.北京：科学出版社，2002：272.

[14]曲通馨.绝热材料与绝热工程实用手册[M].1998：224.

Calculation and Analysis of Heat Transfer Process in Pipes of Altitude Test Facility

ZHU Jian-jun1，DONG Wei1，WU Feng2，TIAN Xiao-jiang2
(1.School of Mechanical Engineering，Shanghai Jiaotong University，Shanghai 200240，China；2.China Gas Turbine Establishment，Jiangyou 621703，China)

Unsteady heat transfer characteristics in pipes of altitude test facility are analyzed,and equa⁃tions of heat transfer between hot air and walls are developed.Moreover,correction method of calculation re⁃sults is offered on the basis of test data comparison.Outlet temperature raising processes at two test condi⁃tions are well predicted by using the method.The results show that local heat loss plays a very important role in the process of pipe network’s heat losing;the temperature of blender outlet should be controlled dif⁃ferently in different periods to reduce test preparation time.

altitude test facility；unsteady heat transfer；numerical simulation；pipe network

V211.72；TK124

A

1672-2620(2011)04-0010-05

2010-09-29；

2011-09-14

航空科学基金(20081057004)

朱剑鋆(1986-)，男，上海人，博士研究生，主要从事流动换热的相关研究。