一种网格概率多目标数据关联算法✴

周航，冯新喜

（空军工程大学电讯工程学院，西安710077）

一种网格概率多目标数据关联算法✴

周航，冯新喜

（空军工程大学电讯工程学院，西安710077）

针对多目标跟踪中数据关联问题，提出了一种基于网格概率的数据关联算法。该算法首先计算出关联门内全部回波的关联系数，然后利用网格概率的思想将关联系数小的有效回波的系数值配权给其它有效回波，同时对于两跟踪波门交叉区域内的有效回波也使用配权法分别分配给两个跟踪波门内的其它邻近回波，最后通过概率加权进行数据关联。仿真结果表明，该算法能够有效解决多目标跟踪中的数据关联问题，并且有较高的关联正确率，而且CPU占用时间较短。

多目标跟踪；网格概率；回波关联系数；有效回波

1 引言

在多目标跟踪中，数据关联是核心问题［1-2］，关联的质量直接影响到目标跟踪效果。目前，已有的统计关联方法主要分为最近邻关联和全关联两大类。最近邻关联是指选择关联门内所有回波中与被跟踪目标的统计距离最近的一个回波作为关联点迹，其它的回波则被丢弃，比如文献［3］中提到的最近邻法；全关联方法认为关联门内所有回波都可能源自目标，因此所有的回波都参与关联，比如文献［4］中提到的JPDA方法。它们各有优缺点：最近邻方法的优点是计算量小，实现简单，而且比较直观，适合用于工程实践，缺点是只适合于稀疏环境，在复杂环境时容易误跟；全关联方法的优点是能够较好地处理目标密度较大的情况，跟踪正确率高，但由于所有的回波都参与关联，计算量大，实时性差，不适合用于工程实践。

综合最近邻方法实时性强和全关联正确率高的优点，本文提出了基于网格概率的数据关联算法，它是一种介于最近邻和全关联之间的算法，采用关联门内全部回波的关联系数，不舍去任何有效回波，将关联系数小的有效回波系数值，通过网格概率的方法配权给其它有效回波，这样参与关联的有效回波并不是全部回波。由于采用了多个回波，因此关联正确率高于最近邻方法［3］；由于不采用所有的回波参与关联，实时性高于全关联方法［4］；再次，因为本文所提供的方法并没有盲目地舍去关联系数小的有效回波，而是让其不参加关联，但其关联系数分配给邻近其它有效回波，这样相比文献［5］，也提高了关联的精度。本文算法规定对于跟踪波门交叉区域内的有效回波值也要使用配权的方法分别分配给两个跟踪波门内的其它邻近回波，这样就避免了PDA方法在跟踪多目标时交叉区域概率重复计算，最终导致多目标航迹跟踪错误。仿真实验表明，该算法能够有效实现数据关联。

2 问题描述

由于传感器在整个量测过程中不可避免地引入量测误差，再加上对于跟踪环境缺乏足够的先验知识，通常不能预先知道被跟踪目标的数目，也不能判断量测数据的真实来源，一般情况下，必须采用数据关联技术来寻求解决办法。数据关联就是确定哪个量测或者航迹来自哪个目标，具体模型如图1所示。

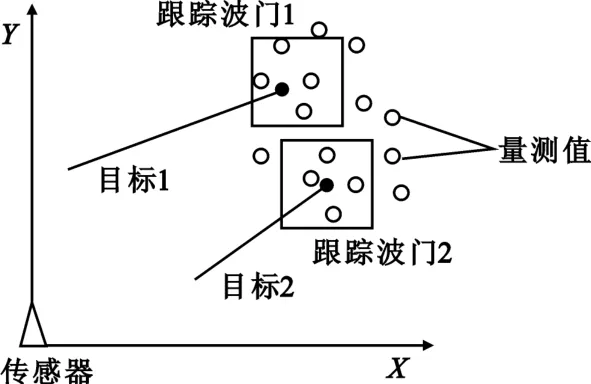
图1多目标数据关联模型Fig.1 Themodel ofmulti-target data association

图1 是多目标数据关联的情形。假设传感器位置为坐标原点，传感器在第k次扫描中获得的观测可表示为{Zi(k)，i=1，2，…，n}，i是传感器在第k次扫描中获得的第i个观测值。

假设目标数为T，对传感器跟踪多目标的情况，使用Kalman滤波，得到了目标j(j=1，2，…，T)在k时刻的测量预测值Z＾j(k／k-1)。以测量预测值为中心，设定跟踪波门，对于矩形跟踪门，若k时刻的测量Zi(k)满足式（1），则称测量Zi(k)为来自目标j的一个有效回波。

式中，σr是残差的标准偏差；K为门限常数，由观测密度、检测概率和状态矢量的维数所确定。σr与测量数据的误差和Kalman滤波器的预测协方差矩阵有关：

式中，σ是测量的标准差，σp是由Kalman滤波器得到的预测标准差。

3 网格概率的数据关联

3.1 网格概率

网络概率的思想是将每一个跟踪波门平均分成N个大小相同的网格，且以预测量测点Z＾j(k／k-1) (j=1，2，…，T)为网格的中心，其它有效回波q (q=1，2，…，jt)分别落在网格内［6］，再计算有效回波到网格中心的距离：通过dqj(k)的大小来分配关联系数θqj。分配规则如下：距网格中心越远，关联系数越小；关联系数θqj满足约束条

具体关联系数赋值表达式如下：

式中，dqj(k)是各有效回波到网格中心的欧拉距离，归一化常数μj( k)可由下式求得：

约束条件为

计算出每个有效回波q的关联系数后，考虑到既要充分利用有效回波所带有的信息，又要避免其太多或精度不高对运算速度和精度造成的影响。所以通过比较可知波门w内的有效回波数最少，假设其回波数为M个，以M为基准，对其它波门内的多余有效回波按以下规则进行处理：

（1）对于波门v(v=1，2，…，T)，假设其有Q个有效回波(Q≥M)；

（2）将关联系数θqj由大到小排列，根据上述原则，保留波门v的前M个关联系数，对于后Q-M个关联系数，逐一分配给所在网格靠近网格中心的邻域，其目的就是将关联系数向网格中心附近的有效回波聚拢，以此来提高关联精度。

具体的网格概率分配规则如图2所示。

图2 关联系数配权示意图Fig.2 Association coefficient distribution schematic diagram

首先判断Q-M个有效回波所在的网格，从权值最小的有效回波开始，逐一将其关联系数分配给该网格8邻域中靠近网格中心的邻域。如果某一邻域内没有有效回波，则不分配权值［7］；如果某一邻域内有多个保留下来的有效回波，则又将该邻域分配到的关联系数平均分给这些有效回波。原则是分配完成后，跟踪波门内的关联系数仍然满

以图2为例进行具体分析。设待分配网格概率权值为θ1，邻域内的两回波权值分别为θ2、θ3。将θ1配权给8邻域靠近中心的网格，因为其有一网格中无回波则不配权；配权后邻域内的两回波权值分别为这样一次配权结束，再进行下次配权过程。

值得注意的是，本算法在处理两个跟踪波门的交叉区域时规定，对于跟踪波门交叉区域内的有效回波值，使用关联系数分配的方法分别分配给两个跟踪波门内的其它不在交叉区域的邻近回波，这样做的好处是避免了交叉区域的有效回波关联系数，在两个跟踪波门内重复使用，避免造成航迹误跟踪。

Bar-shalom等人提出的JPDA方法是在以下两个可行性假设的基础上提出来的：一是对于每一个量测只能源于一个源、目标或杂波，二是每个目标最多只能产生一个回波。但是这两个假设并不符合实际情况［8］。本文所提出的基于网格概率的数据关联算法对量测和目标的关系没有这样的限制。

在实时性方面，JPDA及其改进方法中，将“聚”拆分成每个可行矩阵，这样将耗费CPU大量的时间，影响了关联的实时性，所以，此法不能应用于真正的工程实践当中。在本文提出的方法中，不存在矩阵拆分的问题，所有运算都是普通的代数运算，从而提高了算法的实时性。

在精确度方面，文献［3］中所提出的方法，虽然提高了实时性，但是因为其直接舍掉了部分量测值，所以精度不高。本文的方法虽然在精确度上不及JPDA方法，但不会误跟目标，而且精度也高于文献［3］的方法。

3.2 数据关联

通过3.1节方法，对部分点进行重新配权，每个波门内，关联系数较小的Q-M个有效回波已经舍掉，现在每个波门内的有效回波数是一样的，且其相关系数其具体表达形式如下：

根据跟踪波门内每个有效回波对应的关联系数，获得均值中心Cj() k：

约束条件为

获得了均值中心Cj() k后，就需要对目标的状态进行估计和滤波，最终更新状态，并进入下一个Kalman滤波过程。

4 算法流程

多目标数据关联的具体算法流程如下所述。Step 1：在航迹更新周期开始时，利用式（7）～（10）获取目标j(j=1，2，…，T)的预测状态向量、预测量测向量、新息协方差以及增益。

（1）给定初始值X＾j（0，0）、P＾j（0，0），递推公式由K=1开始；

（2）一步预测状态为

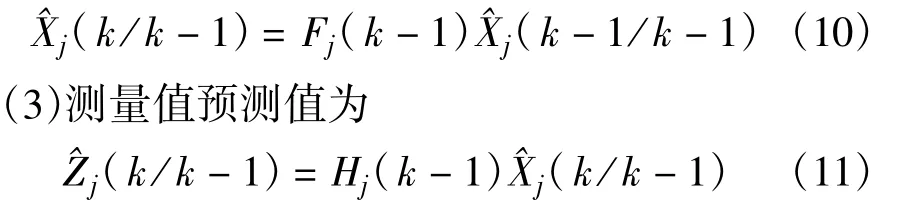
（4）预测协方差矩阵为

Step 2：在进行多目标数据关联计算之前，对所有量测是否落入跟踪波门内进行确认，如果满足

则是有效回波，这里：

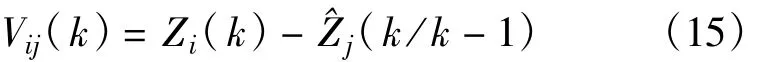
式中，Zi(k)(i=1，2，…，mk)为传感器获得的量测，Vij(k)为量测i对目标j的量测新息，K为跟踪波门的门限值。

Step 3：采用网格概率的方法对落入跟踪波门的有效回波进行分析计算，获得均值中心Cj(k)。Cj(k)的计算过程如下：

（1）对于每一个波门，统计在每一个波门中的量测点个数；

（2）对于目标j，计算落入跟踪波门内的量测到Z＾j(k／k-1)的距离：

（3）通过步骤2中计算的距离值大小，来分配各量测到＾Zjk／k() -1的关联系数θqj，且满足=1；

（4）在j个波门内，以最少量测数M为准，其它j-1个波门内的量测数利用网格概率的方法，将多余的量测点的关联系数以一定的规则配权给邻近的其它保留下来的量测点；

（5）写出关联矩阵：

其中，横坐标代表有效量测，纵坐标代表目标；

（6）通过关联矩阵，对量测值加权求平均，得到均值中心Cj() k。

Step 4：利用式（15）～（18）对各目标的状态和协方差进行滤波更新：

5 仿真与分析

为了验证算法的性能，本文给出单个传感器跟踪交叉运动目标的例子，与传统统计关联算法中最典型的NN算法和JPDA算法在跟踪精度和CPU运行时间上进行对比研究。

设目标的运动模型为

采样时间间隔T=1 s，状态向量X k() +1是包含目标距传感器的距离和速度的四维向量。目标1和目标2的初始状态分别为

接收观测的目标回波由目标真实位置叠加上零均值、协方差为R的高斯噪声产生，R=0.1 km2，每个波门内平均杂波数为17。检测概率Pd=1，门概率Pg=0.99。蒙特卡罗仿真次数为50次。

图3给出了两条原始航迹，图4给出了3种算法对目标1和目标2的跟踪情况，图5和图6分别给出了3种算法对目标1、目标位置均方误差比较图。表1给出了3种算法平均占用CPU的时间；表2给出了通过20次仿真实验，每次实验进行10次MC仿真的3种算法的统计关联正确率。

图3 两个交叉目标的原始航迹Fig.3 Two original tracks of crossing targets

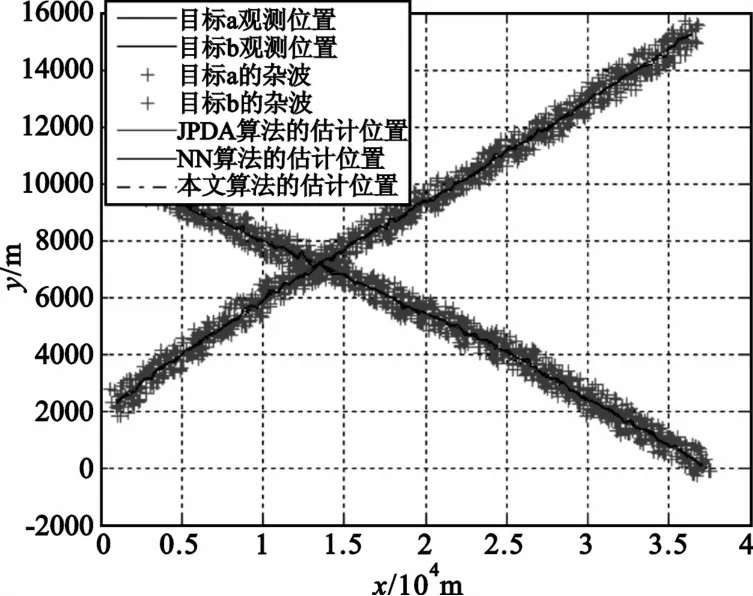
图4 各算法跟踪比较图Fig.4 The results of threemethods

图5 对目标1的位置误差比较图（杂波数为17）Fig.5 Comparison of the RMSerror in position to Target1

图6 对目标2的位置误差比较图（杂波数为17）Fig.6 Comparison of the RMSerror in position to Target2

表1 CPU运行时间对比Table 1 Comparison of CPU running time

表2 算法统计关联正确率Table 2 Ratio of correct association percentage with the threemethods

由图5和图6可知，本文所提出的算法在关联精度上要明显好于NN算法，与JPDA算法相比在关联精度上会比其略低10～20m。这是因为NN算法是一种单关联算法，在对目标进行跟踪的时候，它认定跟踪门内距离波门中心最近的点为跟踪点，在对本文仿真所提供的密集杂波环境下进行关联，必然导致均方误差波动很大；而本文算法是一种全部关联条件下的局部关联算法，虽然能提高关联算法在跟踪精度上的缺点，但是相比于全关联的JPDA算法，精度会略低一些。但由表1可得，在CPU的占用时间上，因为在密集杂波环境中，JPDA算法计算量会成指数增长，所以本文算法CPU时间占用量明显少于JPDA算法。综上两个方面，本文算法优于其它两种典型的统计关联算法。

6 结束语

针对多目标数据关联的问题，本文提出了一种基于网格概率的数据关联算法，该算法的特点是充分考虑到了最近邻关联和全关联这两种数据关联算法的优缺点，通过对跟踪波门内的有效回波进行概率网格配权处理，并对处理后的概率加权，实现最终的多目标数据关联。而且该算法充分考虑到波门交叉区域内的有效回波关联问题，增强了关联的精确度。仿真实验表明了该算法的有效性与可行性，具有一定的应用价值。

［1］Bar-Shalom Y，Fortman T.Tracking and Data Association［M］.New York：Academic Press，1998.

［2］Bar-Shalom Y.MultitargetMultisensor Tracking Applications and Advances（Part I）［M］.Norwood：Artech Press，1990.

［3］杨万海.多传感器数据融合及其应用［M］.西安：西安电子科技大学出版社，2004. YANGWan-hai.Muti-sensor data fussion and application［M］.Xi′an：Xidian University Press，2004.（in Chinese）

［4］何友，王国宏，彭应宁，等.多传感器信息融合及应用［M］.北京：电子工业出版社，2000.HEYou，WANGGuo-hong，PENG Ying-ning，et al.Multi -sensor imformation fussion and application［M］.Beijing：Publishing House of Electronics Industry，2000.（in Chinese）

［5］权太范.目标跟踪新理论与技术［M］.北京：国防工业出版社，2009. QUAN Tai-fan.The new technology of targets tracking［M］. Beijing：National Defense Industry Press，2009.（in Chinese）

［6］Alexiev K M，Bojiliov L V.A Hough Transform Track Initiation Algorithm for Multiple Passive Sensors［C］／／Proceedings of 2007 International Conference on Multisource Information Fusion.Paris，France：IEEE，2000：211-216.

［7］曾昭博，王睿，刘伟.基于模糊平均综合相似度的航迹关联算法［J］.电讯技术，2009，49（8）：9-12. ZENG Zhao-bo，WANG Rui，LIU Wei.A data association algorithm based on fuzzy mean synthetical resembledegree［J］.Telecommunication Engineering，2009，49（8）：9-12.（in Chinese）

［8］张谦.多传感器目标跟踪技术研究［D］.西安：西北工业大学，2007. ZHANGQian.The technology ofmulti-sensor targets tracking［D］.Xi′an：Northwestern Polytechnical University，2007.（in Chinese）

ZHOUHangwas born in Chongqing，in 1988.He is now a graduate student.His research direction ismulti-sensor information fussion.

Email：zhouhang-happy＠126.com

冯新喜（1962—），男，陕西西安人，教授、博士生导师，主要研究方向为人工智能、多传感器信息融合。

FENGXin-xiwas born in Xi′an，Shaanxi Province，in 1962.He is now a professor and also the Ph.D.supervisor.His research interests include artificial intelligence andmulti-s ensor information fussion.

诚聘审稿专家启事

为了进一步加大审稿力度，充实审稿专家数据库，提高办刊质量，本刊常年面向社会诚聘电子信息领域的专家、学者担任本刊的审稿专家。审稿专家将享有如下权利：

（1）向本刊投稿通过评审后优先安排发表，并免收审稿费和版面费；

（2）向本刊推荐稿件通过评审后优先安排发表，并酌情减免版面费；

（3）获得每期免费赠阅的《电讯技术》及本刊编辑部编辑出版的《电讯技术动态》（月刊，内部交流，全彩色铜版纸印刷）；

（4）获得按最高标准支付的审稿费；

（5）参加本刊举办的学术活动。

如果您有意应邀加入到本刊的审稿专家行列，敬请填写附表（可向编辑部索要电子版或在本刊网站www.teleonline.cn下载）后通过电子邮件发送到本刊编辑部邮箱。我们承诺为您的个人信息保密，对于您的支持表示衷心感谢。

电话：028-87555632传真：028-87538378 Email：dianxunjishu＠china.com

《电讯技术》审稿专家登记表

A Multi-target Data Association Algorithm Based on Grid Probability

ZHOU Hang，FENG Xin-xi
（Telecommunication Engineering Institute，Air Force Engineering University，Xi′an 710077，China）

To solve the data association problem in multi-target tracking，a novel gorithm of data association is proposed based on grid probability.First，this algorithm calculates thewhole effective echoes correlative coefficients，then uses grid probability concept to allot the value of effective echoeswith smaller correlative coefficient to other effective echoes.For the effective echoes in interaction area of tracking wave-door，it uses the same method to assign the values to the other adjacent echoeswithin the two tracking wave-doors respectively.Finally the correlative coefficients of the echoes are correlated through probability-weighting.Simulation results show the algorithm can effectively solve the problem inmulti-target tracking，and has a higher accurate rate of association.Besides，the CPU occupies a relatively short time.

multi-target tracking；grid probability；correlative coefficients；effective echoes

Supported by Air Force Armament Department（KJ09131）

姓名单位职务基本信息职称学历学位从事专业通讯地址邮编联系方式电话传真Email QQ号个人简介（科研及学术成就、社会兼职等）

TN953

A

10.3969／j.issn.1001-893x.2011.09.012

周航（1988—），男，重庆人，硕士研究生，主要研究方向为多传感器信息融合；

1001-893X（2011）09-0059-06

2011-03-31；

2011-07-22

空军装备部资助项目（KJ09131）