配电系统可靠性评估方法综述

李 翔

(四川大学电气信息学院，四川成都 610065)

1 概述

配电系统中供电系统部分可以分为输变电和配电两大系统[1]。其中配电系统位于电力系统的末端，包括配电网全部、配电变电所、各种电压等级的配电线路以及接户线等设备。配电网将电源和输变电系统与用户连接起来，是向用户分配电能和供给电能的重要环节。所谓配电系统可靠性，其实质就是研究配电系统本身的可靠性及其对用户供电能力的可靠性。根据电力公司的不完全统计，高达80%的用户故障是由配电系统故障所造成的[1]，因此可以看出，研究配电系统的可靠性无论对工业发展还是民生都具有非常重要的意义。笔者对当今比较重要的集中配电系统可靠性评估算法进行了汇总及比较，旨在为该领域的可靠性研究提供一些借鉴。

2 可靠性指标与计算公式

2.1 负荷点可靠性指标

在电力系统的可靠性评估中，主要采用以下四个指标来反映负荷点的可靠性:(1)年平均停运持续时间U;(2)年故障停运率λ;(3)平均停运持续时间γ;(4)系统及负荷点电量不足期望值ENS。

(1)年平均停运持续时间U。系指负荷点在一年内停电的总时间，反映该负荷点供电的可靠性。系统对负荷点的供电可靠性显然与U值的大小成反比。

(2)年故障停运率λ(次/年)。系指负荷点在一年内由于电网故障而产生停电情况的次数。负荷点λ值的大小与该负荷点供电可靠性成正比。

(3)平均停运持续时间γ(小时/次)。该指标说明了停电后恢复供电的类型，表示为停电开始到恢复供电间隔时间的数值平均值。在有备用元件的情况下，γ值较小，说明停电后恢复供电所需的时间较短。

为了更加清楚的说明这些指标，假设存在一负荷点s，以此为例来介绍如何计算这三个指标:

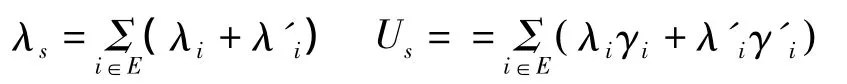
式中 λs代表负荷点s的年平均故障率;Us代表年平均停运时间;λi代表年平均故障率;λ'i代表年平均计划检修率。γi代表平均故障修复时间;λ'i代表平均计划检修时间。λi、λ'i、γi和 γ'i这四个指标都指的是配电网络中第i个元件。则E代表所有元件的集合。

(4)系统及各负荷点的电量不足期望值

计算公式为:ENS=ΣLaiUi

式中 La为负荷点i所带的负荷值，Ui为负荷点i的年停运率。

2.2 系统的可靠性指标

在“系统”的可靠性指标中，“系统”是指“由若干子系统或基本元件有机地联接起来，可完成某种特定功能的整体”，即任何一个电力系统部分有可能是一个独立的系统，也有可能是另一个系统的子系统，具体情况具体分析。现如今国际上通常采用了下列指标来反映电力系统故障停运的严重程度，并且对系统进行总体评估。各指标具体内容及计算公式可参见文献[2]，主要包括:系统平均停电频率(SAIFI)、系统平均停电持续时间(SAIDI)、用户平均停电持续时间(CAIDI)、用户平均停电频率(CAIFI)，平均供电可用率(ASAI)、用户平均停电电量(AEUS)等。

3 常用的配电系统可靠性评估方法

配电系统可靠性评估虽然总体来说起步较晚，但至今在模型和算法上的成熟度已经与当初不可同日而语。目前比较流行的评估方法有故障模式与分析法、网络简化法及近似法等，而能够较为准确地进行评估的方法主要有解析法、蒙特卡罗模拟法、混合法和人工智能方法四大类。

3.1 解析法

解析法[3]作为当今一种主流的配电系统可靠性评估方法目前在全世界被广泛应用。该方法的基本原理:首先建立针对该系统的可靠性概率模型，然后利用故障枚举的方式进行故障状态的选择，之后用各种适用数学方法求解该模型，最后得出该系统的可靠性指标。当使用解析法时，一般来说先通过按某种逻辑逐个选择系统故障的停运状态。下面介绍几种比较重要的解析法。

(1)故障模式后果分析法。故障模式后果分析法[4][5]又名 FMEA 法，是用于配电系统可靠性评估的传统方法。该方法主要用于对简单辐射型主馈线的可靠性评估计算。其基本步骤为:①产生(或枚举)系统网络可能的故障事件;②对每一个故障事件，进行系统网络的行为分析，形成系统网络的失效事件集;③根据所形成的“系统网络的失效事件集”，结合元件的可靠性数据，累积形成系统可靠性指标。

FMEA法的简明流程见图1。

图1 FMEA法简明流程图

馈线上可能有开关、用户变压器、线路三类元件故障，因此，考虑一段线路上所有可能出现的故障事件，再结合元件可靠性数据，即可得到一段线路上(假设为第k段)所有故障事件引起的用户停电持续时间(时户数):

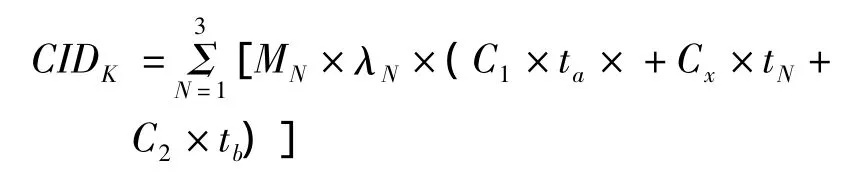
式中 MN为该段上第N类元件的台数(线路取平均分段长度，用户变压器数取台数，开关一般为一个);λN为第N类元件的故障率;ta为出线开关、分段开关操作时间;tN为第N类元件的故障排除时间;tb为联络开关操作时间;C1为在故障段之前能由母线恢复供电的用户总数;C2为在故障段之后能由联络线恢复供电的用户总数;Cx为在故障期间不能恢复供电的用户总数。

利用上式逐一计算馈线中各段的用户停电持续时间，将其综合起来，便能够计算出该馈线上的用户停电持续时间和系统用户停电总持续时间等可靠性指标。

该方法原理简单，能够直接用于简单辐射形配电系统的可靠性评估计算中。但是，由于该方法在系统复杂时系统状态会呈指数形式增加，因此，FMEA法一般不能用于复杂的辐射形配电网的评估计算。

(2)网络等值法。在现实生活中，往往是主馈线和副馈线共同构成实际的配电网络，这种配电网络结构相当复杂，进行可靠性评估计算非常繁琐。基于以上考虑，为了解决这种复杂配电系统可靠性评估问题，R.Billinton和 P.Wang提出了网络等值法。文献[6]中详细介绍了一种通过网络等值法对复杂网络进行等效简化的方法，它从最低一级的子馈线开始，首先对馈线进行分层处理，在分层工作完成后，任意一条馈线及该馈线所连接的各种元件均属于同一层，然后以每一层作为等效分支线逐次向上层等效，直到线路不带子馈线为止，然后再用下行等效和FMEA法得到所有负荷点的可靠性指标，最后综合各个负荷点的可靠性指标而得到系统的可靠性指标。

笔者认为:在辐射形的配电系统中，系统结构往往比较复杂，而网络等值法正是针对这种弊端进行网络化简，能够大大简化计算过程。但是，该方法没有考虑各分支馈线首端所设断路器的影响，在分支馈线比较多的情况下，就需要运用非常大的计算量来等效馈线，计算相当复杂。

(3)基于故障扩散的算法[7][8][9]。该方法的建立是以故障后果分析法为基础的，它通过合理的运用基于故障扩散和遍历的技术，可以将配电系统中所有的节点按照故障类型的不同而划分为若干区域，然后通过判断各种不同故障类型的影响范围进行可靠性评估。在任意故障事件发生后，可以把各个节点按是否故障及故障时间的区别总共分为四大类[10]:a类节点，即正常节点，可以定义为不受故障事件影响的节点;b类节点可以定义为故障时间为隔离操作时间的节点;c类节点由两部分组成，它被定义为故障时间为隔离操作和切换操作时间两部分相加的节点;d类节点则可以定义为故障时间为元件修复时间的节点。

在图2所示的系统中，s1～s5为隔离开关;b1、b2为断路器;AS为备用电源;c1为联络开关;p1～p4为负荷节点;r1～r4为熔断器。

表1中列出了针对图2网络发生故障后实现的节点分类，包括故障线路、相应的动作隔离开关和负荷节点类型。①～⑥为可能发生故障的线路。

文献[11]为了使评估方法更加适应系统不同自动化程度的要求，考虑增加了隔离开关为自动或手动两种模式的情况。文献[12]的目的是节省故障枚举时重复搜索单个元件的时间，为此，利用了通过邻接矩阵的构造从而将节点分成若干块的方法，以块为单位进行分析，相对提高了搜索效率。该方法考虑了系统中断路器、隔离开关、备用电源等设备配置的影响，通过故障后各分块子系统中有无电源及切换开关的判断，较容易确定节点故障的类型。但是，该算法在前向搜索断路器时采用了潮流计算，大大增加了计算量，还有待于提高。

表1 故障后节点分类表

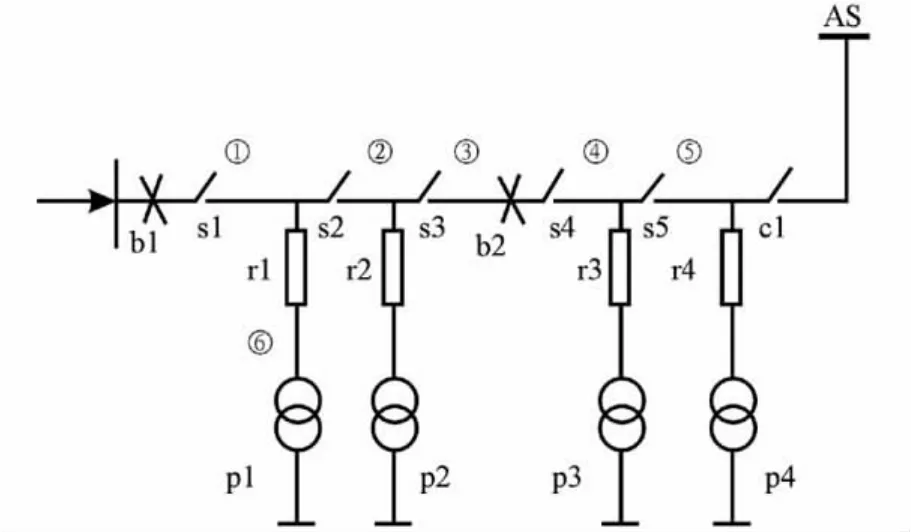
图2 简单辐射型配电网示意图

(4)递归算法[3]。递归算法利用了配电系统中的的基本结构为树状特点，将原本普通的配电系统各个数据按照树型储存，然后对系统树进行递归遍历，进而对遍历后的子馈线进行可靠性等值，最后达到简化原来复杂网络的目的。这样一来，通过其他的算法，就能更有效率地计算出配电系统的可靠性指标。

(5)最小路法[1]。所谓最小路，即是负荷点与电源之间的最短通路。而最小路法的基本思想同样是出于先对配电系统网络进行简化。具体方法是对先求取要到每一负荷点所经过的最小路，然后分离出除最小路之外的所有非最小路，将非最小路上的各种影响指标等效到已经求出的最小路上，最后沿着最小路进行计算，即可方便地求出各种所需数据。

最小路算法有一套适用于自己的可靠性指标计算公式，即:

式中 γi为元件i的平均故障修复时间;λi为元件i的年故障率;λ'i为元件i的年平均计划检修率;γ'i为元件i的平均计划检修时间;λs为系统的平均故障率;us为系统的年平均停运时间;γs为系统的平均停运持续时间。

最小路法一般配合其他评估方法共同使用，在为复杂网络化简的过程中给用户提供了更多的选择。

(6)其他配电网可靠性评估方法。

除了上述几种常用的配电系统可靠性评估方法外，如今众多学者还提出了如布尔展开定理法、全概率公式法和网络规划法等评估方法。但是，这些方法对配电可靠性管理人员来说大多比较复杂，不易掌握。同时，由于故障诊断及恢复供电时间等对可靠性指标有着重要的影响，于是，在提高可靠性的理论研究中如何快速隔离故障及恢复供电等问题上，国外在这方面作了许多探讨，国内的许多学者也对此提出了不少方案，如节点一阶负荷矩法。此外，国内外不少学者在如何进行网络重构等方面也作了不少研究，如基于规则的专家规划方法和基于最优化算法的方法，通过分段开关及联络开关的换接进行网络重构，使负荷能够转移，保证非故障区段始终能正常供电。在算法方面，还有如非线性的分支定界法、线性迭代法、遗传算法等，都在不断的研究中。

解析法多种多样，但在实际情况中，系统常常非常复杂。由于系统内元件数目增加，系统状态的数目往往会成指数形式增长，总的计算量将会相当大。为解决这种情况，在实际应用中，一般可采取一些能够有效减少计算量的算法，主旨在于先简化或划分复杂网络，再进行可靠性评估计算。

3.2 模拟法

模拟法与解析法相比而言较为直观，它先对元件概率分布采样进行状态的选择和估计，然后利用统计学的方法得到可靠性指标。这种方法便于处理负荷的随机变化特性。但是，其计算时间与计算精度紧密相关，且具有明显的统计性质，因此，为了得到比较接近实际的模拟结果，模拟运算量很大，往往需要非常长的计算时间。但随着高速计算机的应用，该方法已经成为一种可行的技术。

蒙特卡罗模拟法[13]、[14]、[15]的过程是先用数值计算方法模拟系统的实际运行过程，然后观察模拟过程和元件寿命的实际情况，处理后得到所求系统的可靠性指标。

蒙特卡罗法属于统计实验方法，便于研究人员掌握和理解，尤其是针对系统按时间顺序进行评估操作更是游刃有余，相比解析法具有的一个优势就是其计算量几乎不受系统规模和复杂程度的影响。

随着全国的电网联网，系统规模越来越大，因此系统的建模越来越困难，计算也更为复杂。以蒙特卡罗法为代表的模拟法能够较好地解决这些问题，因此被广泛应用。

3.3 混合法

模拟法和解析法均为比较常用的方法，但其各自又有鲜明的缺点。模拟法适合于涉及到大量低可靠性的元件且容易发生多重故障的系统，而解析法往往用于网络规模较小的系统。在当今学者的研究中发现，如果能够提出一种有效的、能将两种方法有机地结合起来的方法，便能够取长补短。在这种思想的倡导下，混合法应运而生。Clancy D P首先将混合法应用于多区域电力系统的可靠性评估[16]。该方法的主要思路是:应用模拟法，以降低模拟统计量的方差和CPU时间，在其他可以使用解析法的地方再利用解析法。

由于这种方法新颖有效，此后，许多学者对混合法都进行了较为深入的研究:Li wenyuan和Billiton R等人提出了随机模拟的方法。还有许多研究人员都作出了相当大的努力。文献[17]提出了一种解析法和模拟法相结合的可靠性评估方法，具体来说，该方法先借用解析法中的网络等值法来简化网络，然后在计算时采用蒙特卡洛模拟法进行计算，并将两种方法所求出的可靠性指标进行结合。文献[18]提出的方法主要是在利用模拟法求解时，同样要参考解析法能够获取的独特信息，作用同样是丰富算法。

随着配电系统的结构日益复杂，单独的一种方法已经愈发无力地解决评估问题，因此，将混合法应用于配电系统的可靠性评估，必将是一个很有前途的研究方向。

3.4 人工智能算法

人工智能算法出现的亦比较早。1956年，美国的McCarthy和Minsky等人提出了通过仿效生物处理模式获取智能信息处理功能来快速有效的解决各种难题的方法，经过学者们多年努力，已经有了很大发展。

人工智能算法主要有人工神经网络算法[19]和模糊算法[20]两种，这两种算法的出发点和思路都比较新颖，在可靠性评估的过程中的某些方面都具有自己独特的优势，但由于其面世时间不长，因此还需要众多学者及研究人员进一步探讨分析后才能大规模应用于实际生产工作中。

笔者在对相关文献进行大量阅读后，认为神经网络法等人工智能算法的引入有利于促进配电系统可靠性研究的进一步发展。但该种方法毕竟属于新方法，无论是可操作性还是实用性都待进一步的探索研究与验证。目前来讲，笔者倾向于网络等值法配合最小路法进行结合，前者可以将大型复杂网络进行简化，后者则根据简化后网络的实际情况，将非最小路上的元件故障对负荷点可靠性的影响折算到相应的最小路节点上，从而对于每个负荷点，仅对其最小路上的元件与节点进行计算即可得到负荷点相应的可靠性指标。这种结合的算法考虑了分支线保护、隔离开关、分段断路器的影响，也考虑了计划检修的影响，并且能够处理有无备用电源和有无备用变压器的情况。由于笔者才疏学浅，该方法依然有很大的完善空间，恳请各位读者批评指正。

4 结语

(1)电力系统可靠性评估是从电力系统规划、设计和运行等实践活动中提出来的课题。在电力系统中，配电系统由于直接与用户相连，对供电可靠性的影响最大，因此，对配电网进行可靠性评估是未来电网改造管理工作中的重中之重。配电系统的可靠性评估近年来的发展已经比较完善，但仍有许多可创新之处值得深入讨论研究。

(2)传统的解析法和模拟法应用较为成熟，但随着现代电力系统的日益增大，单纯的一种方法的计算速度将会无法满足需求，因此，多种方法结合将是未来评估方法的发展方向。

(3)人工智能算法是一个新的领域，虽然目前可行性和实用性还不如传统方法，但可以相信，其未来的发展前景将是非常好的。

[1]陈文高.配电系统可靠性实用基础[M].北京:中国电力出版社，1998.

[2]Billinton R，Billinton J E.Distribution system reliability indices.IEEE Transaction on Delivery，1989，4(l):561 －568.

[3]徐其迎.配电网可靠性评估与网络重构的研究[D].广东工业大学检测技术与自动化装置专业，2004.

[4]杨莳百，戴景宸，孙启宏.电力系统可靠性分析基础及应用[M].北京:水利电力出版社，1986.

[5]石 伟.配电网规划及其可靠性评估[D].广东工业大学控制理论专业，2003.

[6]Billinton R，Wang P.Reliability network equivalent approach to distribution system reliability evaluation[J].IEE Proc － Gener.Trans.Distrib，1998，145(2):149 －153.

[7]郭永基.电力系统可靠性分析[M].北京:清华大学出版社，2003.

[8]黎晓刚，张 焰.配电网供电可靠性的递归算法.全国高等学校电力系统及其自动化专业第十五届学术年会论文集[C]，武汉水利电力大学，1999:47－51.

[9]Billinton R，Allan R N.Reliability Evaluation of Power Systems[M].Boston，Pistman，1984.

[10]谢开贵，周平，周家启，等.基于故障扩散的中压配电系统可靠性评估算法[J].电力系统自动化，2001，25(4):45 －45.

[11]李卫星，李志民，刘迎春.复杂辐射状配电系统的可靠性评估[J].中国电机工程学报，2003，23(3):69 －73，79.

[12]刘柏私，谢开贵，马春雷，等.复杂中压配电网的可靠性评估分块算法[J].中国电机工程学报，2005，25(4):40 －45.

[13]郭永基.电力系统可靠性原理和应用[M].北京:清华大学出版社，1983.

[14]Billinton R，Wang P.Teaching distribution system reliability evaluation using monte carlo simulation.IEEE Trans on power systems，1999，14(2):397 －403.

[15]Liang X，Goel L.Distribution system reliability evaluation using the Monte Carlo simulation method.Electric Power systems research，1997，40(2):75 －83.

[16]Clancy D P，Gross G，Wu FF.Probabilistic Flows for Reliability Evduation of Multi-Area Power system Interconnection Electrical Power＆ Energy Systems 1983，5(2):101～114.

[17]万国成，任 震，吴日异，等.混合法在复杂配电网可靠性评估中的应用[J].中国电机工程学报，2004，24(9):92－98.

[18]别朝红，王秀丽，王锡凡.电力系统可靠性评估的混合法研究[J].中国电力，2001，34(3):25 －28.

[19]Chen C，Chen J.A Neural Network Approach for Evaluation Distribution systems Research Electric Power systems research，1993(26):255－229.

[20]张 焰，电网规划中的模型可靠性评估方法[J].中国电机工程学报，2000，20(11):77－80