遗传算法改进灰色RBF模型在负荷预测中的应用

吴曦 袁荣湘

(武汉大学 电气工程学院，湖北 武汉 430072)

0 引言

电力系统负荷预测是电力规划、控制和运行等工作的重要组成部分。准确的负荷预测有利于提高电网运行的安全稳定性，有效地降低发电成本，增强供电可靠性，从而提高电力系统的经济效益和社会效益。因此，提高负荷预测精度具有重要意义。

负荷预测的方法很多。灰色模型作为一种常用的负荷预测方法，具有要求数据少、不考虑分布规律、不考虑变化趋势等优点，在电力负荷预测中应用越来越广泛［1-3］。但是，当数据离散度大时，数据灰色变大，预测精度变差，不适合于中长期电力负荷预测。径向基函数(RBF)神经网络是一种性能良好的前向网络，既有生物背景，又与函数逼近理论相吻合，具有逼近非常复杂的非线性函数的功能，但过度的拟合逼近往往影响网络的泛化能力。将灰色模型与RBF神经网络结合一定程度上能实现双方的互补，但结合时存在局部最优和收敛性问题一直没有很好的解决［4-6］。

本文利用遗传算法鲁棒性强、收敛速度快以及全局定位能力强的优点［7-10］，代替传统的最小二乘法对GM(1，1)中的参数进行优化求解，可以避免陷入局部最优，从而实现全局寻优，而且改进后的模型相结合时收敛速度更快，精度更高。并举例将该模型首次在电力负荷预测中应用，发现具有很好的效果。

1 GM(1，1)传统建模

设原始序列为{x(0)(1)，x(0)(2)，…，x(0)(n)}，一阶累加生成序列{x(1)(1)，x(1)(2)，…，x(1)(n)}，其中(i)。其中k=1，2，…，n。由于x(1)(k)具有指数增长规律，故满足一阶线性微分方程模型取时刻k和k+1的平均值上式微分方程对 k=1，2，…，n 的结果写成矩阵形式，

有 Yn=BA，式中

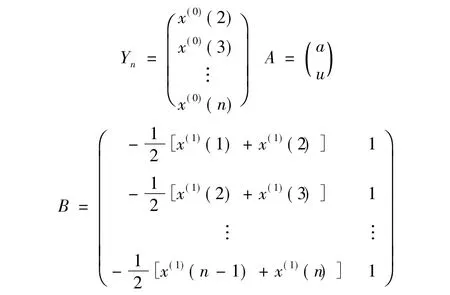
用最小二乘法得到最小二乘近似解，有Yn=BA+E，式中，E为误差项。利用矩阵求导公式，可得

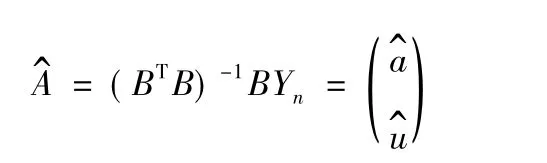
得到的数据解是

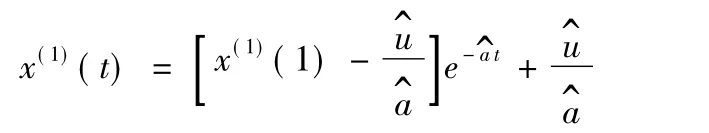
再做累减还原，得原始数列{x(0)(1)，x(0)(2)，…，x(0)(n)}的灰色预测模型为

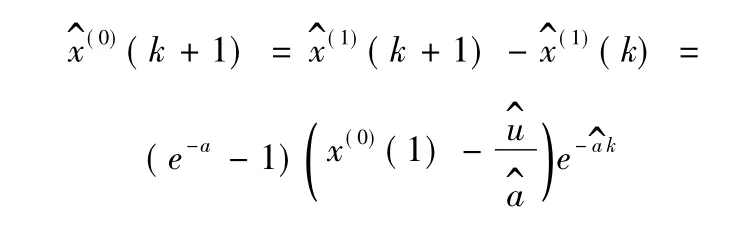
由上述计算过程［11］可知，在数据处理的过程中，背景值用［x(k+1)+x(k)］来代替，这个背景值的设定其实是不够精确的。若设灰导数x(0)(k)=x(1)(k)-x(1)(k-1)是ωk的导数，它相应的背景值应该是 x(1)(ωk)=λkx(1)(k-1)+(1-λk)x(1)(k)，λk∈(0，1)其中 λ1，λ2，…，λn具有高度的非线性关系，用常规方法很难解出。遗传算法自身具有鲁棒性强、收敛速度快以及全局定位能力强的功能，能够很好解决这一问题，使该灰色模型的拟合程度和预测模型精度得以提高［12］。

2 遗传算法改进建模

2.1 个体编码

鉴于实数编码对函数优化问题最为有效，本文个体编码采用实数编码方案，即染色体上的每位基因用一个大于0小于1的实数表示。

2.2 随机产生初始群体

取群体规模为50，应用随机试验，产生初始群体 λi=(λi，1，λi，2，…，λi，n)，i=1，2，…，50

2.3 计算个体的适应值

对应于个体 λi，i=1，2，…，50，设

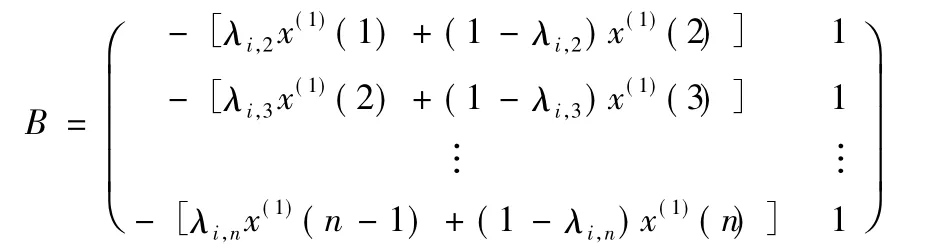
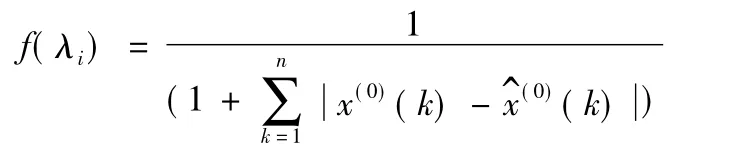
2.4 选择操作

2.5 交叉操作

对已经选择的个体随机选择交配对象，将该交配对象用凸杂交的方法进行交叉操作。具体说来，对随机选择的一对个体λ1和 λ2，令 λ'=x1λ1+x2λ2，其中 x1+x2=1，x1＞0，x2＞0。

2.6 变异操作

为使遗传算法具有局部随机搜索能力以及维持群体的多样性，以一很小变异概率 Pm选择个体的某一位，用一个大于0小于1的随机数取代之。本文选取Pm=0.13。

2.7 终止操作

计算新一代的群体是否能够让灰色模型达到需要的精度。若能够达到要求，则停止运算，若不能达到要求，则继续执行(2.3)，直至合乎要求［13-16］。

3 遗传算法改进的灰色RBF神经网络

3.1 径向基函数RBF简介

RBF神经网络是一种局部神经网络，训练样本需求量比通常的BP网络要少，比全局网络具有更好的建模精度，因此本文采用RBF神经网络。从结构上说，RBF神经网络是单隐层的前向网络，由三层构成:第一层是输入层，第二层是隐含层，第三层是输出层。通常以高斯函数作为RBF径向基函数的基函数，可表示为:

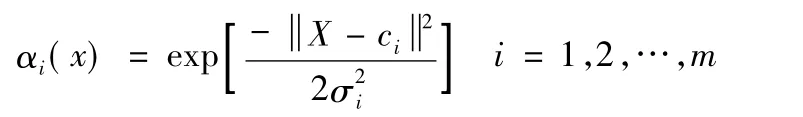
式中αi(x):第i个隐层节点的输出;X:输入样本，X=(x1，x2，…，xn)T;ci:第i个隐层节点的高斯核函数的中心且与X具有相同的维数;σi:第i个隐层节点的变量，称标准化常数，或基宽度;m:隐层节点的个数。

3.2 常规灰色RBF建模

常规灰色RBF建模过程如下。首先分别对多个序列用灰色GM(1，1)模型预测后，会得到一系列的预测值。然后将些数据用公式进行归一化处理。将灰色模型归一化后的拟合值作为RBF神经网络模型的输入样本，实际值作为输出样本，对RBF神经网络进行训练，可以得到各层各个节点的权值和阀值，将GM(1，1)模型对下一时刻或多个时刻的的预测值作为神经网络的输入，得到相应的输出为下一时刻或多个时刻的最终预测值［17］。

3.3 改进后的灰色RBF建模

设用遗传算法改进的灰色模型为IGM(1，1)。归一化方法同上。然后用IGM(1，1)模型归一化后的拟合值作为输入样本，实际值作为输出样本，对RBF神经网络进行训练。可以得到各层各个节点的权值和阀值。将IGM(1，1)对下一时刻或多个时刻的预测值作为神经网络的输入，得到相应的输出为下一时刻或多个时刻的最终预测值［18］。

4 在负荷预测中的应用举例

某市04-09年各月的负荷值如表1所示。

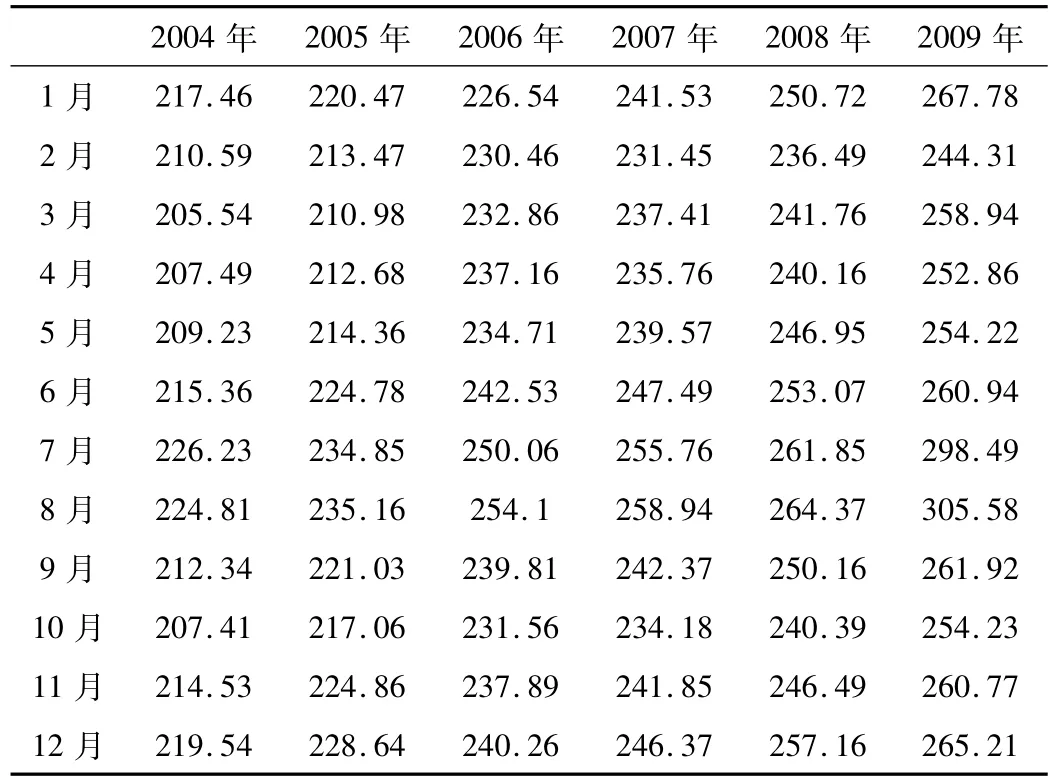
表1 某市04-09年各月的负荷值 单位:MW

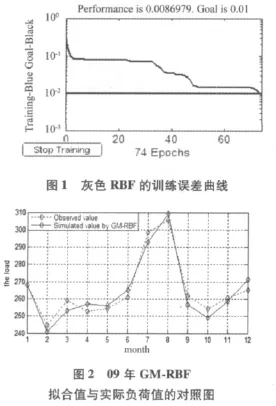
先用传统的灰色模型计算得到原始数据的拟合值。然后将其进行归一化处理。将归一化后的2004年至2008年的5组拟合值作为输入样本，这五年的实际负荷数据的归一化值作为相应的输出样本训练GM-RBF神经网络。设计径向基函数网络时，本文采用MATLAB7神经网络工具箱提供的newrb( )函数来设计。newrb( )函数的代码为 net=newrb(P，T，GOAL，SPREAD)，它的优点在于它一次循环只产生一个神经元，而且每增加一个径向基神经元，都能最大程度的降低误差。故我们从0个神经元开始训练，通过检查输出误差使网络自动增加神经元。检查新网络的误差，重复这个过程直到达到误差要求为止。选取GOAL=0.01。灰色RBF的训练误差曲线如图1所示。

由图1可知，经过 74次训练，网络训练误差为 0.008 697 9，达到了误差目标要求。

用灰色模型对09年的预测值作为输入样本，经过训练好的灰色REF模型运算处理，得到的用电负荷与09年的实际负荷数据比较结果如图2所示。

我们用遗传算法改进灰色模型，用改进后的灰色模型计算原始数据的拟合值，并将归一化处理过的2004年至2008年的5组拟合值作为输入样本，这5年的实际负荷数据的归一化值作为相应的输出样本训练IGM-RBF神经网络。仍然选取GOAL=0.01，遗传算法改进的灰色RBF训练误差曲线如图3所示。

由图3可知，经过13次训练，网络误差为0.00847999，达到误差目标要求。

用改进后的灰色模型对2009年的预测值作为输入样本，经过训练好的IGM-REF模型运算处理，得到的用电负荷与2009年的实际负荷数据比较结果如图4所示。

两种方法的误差比较曲线图如图5所示。

为了更准确得反映，下面给出了误差比较表。

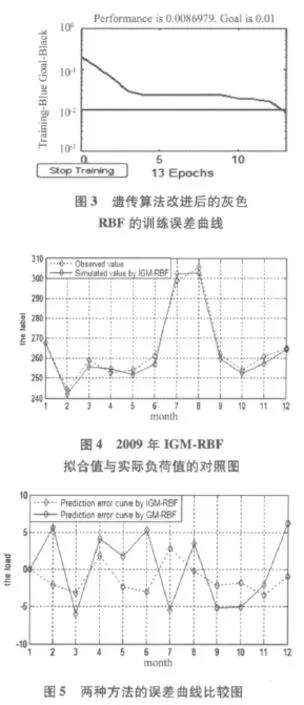
表2 两种预测方法误差比较表

由表2可知，遗传算法改进后的灰色REF模型比未改进的灰色模型具有更快的收敛速度。而且遗传算法改进的灰色REF模型的相对误差和均方根相对误差均小于为改进的模型计算出的误差，可知改进后的灰色REF模型具有更好的精度。

5 结束语

经遗传算法改进的灰色RBF模型，能够避免陷入局部最优，实现全局最优。改进的灰色RBF模型比未经改进的灰色RBF模型的对未来值的预测精度更好，能够有效地降低了误差。因而在电力系统领域负荷预测方面追求更高京精度时，可以采用这一方法。

［1］Lu M，Wevers K.Grey system theory and applications:A way forward［J］.Journal of Grey System，2007，10(1):47-53.

［2］Mendes R，Mohais A S.DynDE:A differential evolution for dynamic optimization problems［C］.Proceedings of 2005 IEEE Congress on Evolutionary Computation，Edinburgh.2005:2808-2815.

［3］车东晓.电力负荷预测技术及其应用［M］.北京:中国电力出版社，2009:171-178.

［4］郭伟伟，刘家学，马云龙，等.基于改进RBF网络算法的电力系统短期负荷预测［J］.电力系统保护与控制，2008，36(23):45-48.

［5］师兵兵，段哲民，陆正俊.神经网络预测中长期电力负荷对比研究［J］.继电器，2007，35(23):43-45.

［6］郑文琛，吉培荣，罗贤举.改进无偏GM(1，1)模型及其在中长期电力负荷预测中的应用［J］.继电器，2008，36(5):36-39.

［7］张筠莉.现代医院门诊量的灰色RBF神经网络预测［J］.计算机工程与应用，2010，46(29):225-228.

［8］琚亚平，张楚华.基于人工神经网络与遗传算法的风力机翼型优化设计方法［J］.中国电机工程学报，2009，29(20):6-11.

［9］崔光照，李小广，张勋才，等.基于改进的粒子群遗传算法的DNA编码序列优化［J］.计算机学报，2010，33(02):311-316.

［10］袁景凌，李小燕，钟珞.遗传优化的灰色神经网络模型比较研究［J］.计算机工程与应用，2010，46(2):41-43.

［11］Cui G Z，Qin L M，et al.Modified PSO algorithm for solving planar graph coloring problem［J］.Progress in Natural Science，2008，18(3):353-357.

［12］玄光男，程润伟.遗传算法与工程优化［M］.北京:清华大学出版社，2004.

［13］庄健，杨清宇，杜海，等.一种高效的复杂系统遗传算法［J］.软件学报，2010，21(11):2790-2801.

［14］Cui G Z，Niu Y Y，Wang Y F，et al.A new approach based on PSO algorithm to find good computational encoding se-quences［J］.Progress in Natural Science，2007，17(6):712-716.

［15］邓亮，赵进，王新.基于遗传算法的网络编码优化［J］.软件学报，2009，20(8):2269-2279.

［16］文艳，宋宗勋，张国柱，等.基于灰色关联-神经网络模型的城市电力负荷短期预测的研究与应用［J］.继电器，2005，33(19):36-40.

［17］张鑫波，李广伟，孙丽基.于RBF辨识的模糊神经网络控制器的设计与实现［J］.计算机仿真，2006，(05):149-153.

［18］董泽，黄宇，韩璞.量子遗传算法优化RBF神经网络及其在热工辨识中的应用［J］.中国电机工程学报，2008，28(17):99-104.