永磁同步电机的自适应神经模糊推理控制研究

张宇 刘凤春 牟宪民

(大连理工大学 电气工程学院，辽宁 大连 116023)

0 引言

由于永磁同步电机(PMSM)具有体积小、结构简单、转动惯量小、输出转矩大、响应速度快、可靠性高等特点，因此在伺服控制领域中得到广泛应用。对此，研究者们提出了许多控制方案，如文献［1］利用矢量控制来进行转矩电流和励磁电流之间的解耦，文献［2］采用滑模变结构控制来克服电机的非线性，文献［3］采用基于自抗扰控制器来设计永磁同步电机的位置伺服系统。这些方法是基于解耦线性化模型的现代控制策略［4］，是从电机本体参数出发进行线性化的处理。

同时从智能控制方法出发，出现了如文献［5］中所采用的模糊PI控制等。但是模糊推理系统的设计却存在相当依靠专家或操作人员经验和知识的缺陷。Jang J-S R.首先提出了自适应神经模糊控制器(ANFIS)［6］，把神经网络和模糊控制相结合，利用神经网络的学习能力与映射能力，实现模糊系统的自学习、自适应功能，并对非线性系统建模进行了仿真研究。文献［7］中把模糊推理和神经网络相结合，进行了永磁同步电动机直接转矩控制的仿真研究，文献［8］把其应用到了中央空调水系统节能控制的仿真研究中，文献［9］把其应用到了开关磁阻电机的控制中。

本文永磁同步电机伺服系统采用双闭环矢量控制来实现，其中用ANFIS速度控制器来取代常规的PI速度调节器，并对其控制过程进行了研究分析。

1 PMSM的矢量控制

矢量控制就是以旋转的转子磁通矢量为参考坐标，利用从定子坐标系(abc坐标系)到转子坐标系(dq坐标系)之间的变换，将三相耦合的定子电流转化为转子坐标系下相互正交的励磁电流id和转矩电流iq。变换方程如下

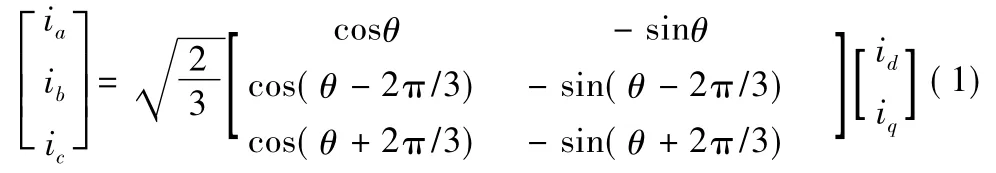
式中，ia、ib、ic为定子三相电流;id、iq分别为 dq 轴定子电流;θ为转子位置信息。

通过坐标变换可得PMSM在矢量控制下电磁转矩方程

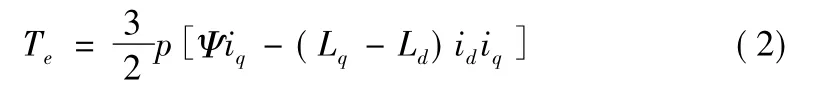
式中，Ld、Lq分别为定子dq轴同步电感，是与(θ无关的常量;Ψ为转子磁链;p为磁极对数。

由 公式(1-2)可知，若令id=0，则电磁转矩完全由转子磁链和定子交轴电流分量确定。控制这两个解耦的量，就控制了电磁转矩，从而控制转速。因此，通过矢量变换实现了像控制直流电机一样地对PMSM进行控制。图1是永磁同步电机伺服系统的双闭环矢量控制系统框图，其中用速度控制器采用的是常规的PID控制。

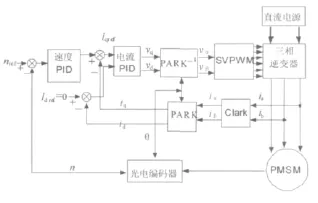
图1 PMSM双闭环矢量控制系统框图

2 自适应神经模糊推理系统(ANFIS)

2.1 ANFIS 原理

尽管模糊推理系统的设计并不主要依靠对象的模型，但是模糊规则的选取却相当依靠专家或操作人员的经验和知识。规则选取的好坏，直接影响控制器的控制效果。神经网络系统具有自学习能力的优点。应用这种自学习的方法对系统模型进行分析与建模，形成了自适应的神经网络技术。自适应的神经网络技术对于模糊系统的建立(模糊规则的建立)是十分有效的工具。自适应神经模糊推理系统(ANFIS)正好结合了模糊控制和神经网络技术两者的优点。

2.2 基于ANFIS控制的PMSM的系统结构

永磁同步电机伺服系统采用双闭环矢量控制，其 中用ANFIS速度控制器来取代常规的PI速度调节器，电 流控制器采用 PI，采用SVPWM技术调制控制电流。原理图如图2所示。

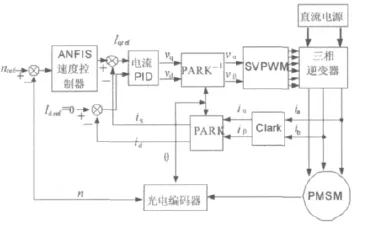
图2 基于ANFIS控制的系统原理图

2.3 ANFIS速度控制器设计

本文中ANFIS是基于Takagi-Sugeno模型的自适应神经模糊推理系统，其网络结构如图 3 所 示［10］。结合本文要求进行如下设计。

第一层为输入层。该层的各个节点直接与输入向量的各分量xi连接，它起着将输入值x=［x1，x2，…，xn］T传送到下一层的作用。该层的节点数N1=n。在本文中n取2，即x1为速度误差e，x2为速度误差变化率ec。

第二层每个节点代表一个语言值变量，如NB、PS等。它的作用是计算各输入量属于各语言变量值模糊集合的隶属函数，且

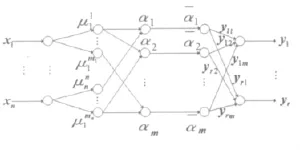
图3 基于T-S模型的模糊神经网络简化结构图

式中，i=1，2，…，n;j=1，2，…，mi。n 是输入量的维数，mi是 xi的模糊分割数。例如，若隶属函数采用高斯函数表示的铃形函数，则

式中，cij和σij分别表示隶属函数的中心和宽度，该层的节点总数本文中 n 取 2，m1、m2都取 7，所以 N2=14。

第三层的每个节点代表一条模糊规则，它的作用是用来匹配模糊规则的前件，计算出每条规则的适应度，即

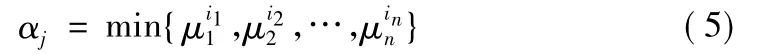
第四层的节点数与第三层相同，即N4=N3=m，它实现的是归一化计算，即

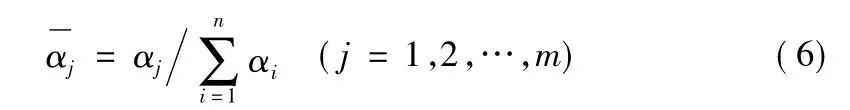
第五层为输出层，它所实现的是清晰化计算，即

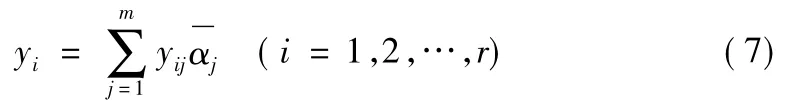
这里的yij是相当于yi的第j个语言值隶属度函数的中心值。

2.4 学习算法

该模糊推理系统利用BP反向传播算法和最小二乘算法来完成对输入/输出数据对建模训练。

ANFIS学习算法流程如图4所示。训练过程由两步组成:第1步，每一次迭代中，输入信号沿网络正向传递至第4层，固定条件参数，然后采用最小二乘法估计结论参数，信号继续正向传递至输出层即第5层;第2步，将获得的误差信号沿反向传播，利用误差反向传播算法调整前件参数。这样不仅可以降低误差反向传播算法中搜索空间的维数，还可以大大提高参数的收敛速度。

3 仿真过程

ANFIS系统通过对大量已知数据的学习得到，因此仿真过程首要任务是采集训练数据。本文为了采集数据成功训练神经网络，设计了模糊PID控制系统，并采集了516组速度误差e，速度误差变化率ec和速度控制器输出组成的数据组作为训练数据，同时从中抽取103组作为测试数据。和ec的模糊化e都取7个语言变量值，经训练可得到基于ANFIS的速度控制器模型。形状如图5所示。

得到 ANFIS模型后组建仿真系统。电机参数如下:电机定子电阻RS=2.875 Ω，交直轴电感Ld=Lq=8.5 mH，转子磁链Ψ =0.175 Wb，磁极对数 p=4，转动惯量 J=0.8 g·m2，额定转矩为 2.8 N·m。

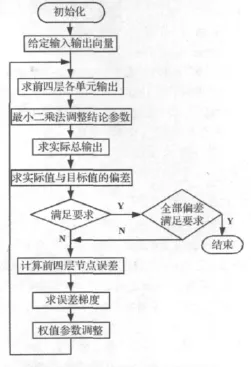
图4 ANFIS训练算法流程图

图5 ANFIS系统模型图

为了便于控制性能的对比，设计了PID控制器、模糊 PID控制器和自适应神经模糊控制器三种控制器。速度控制器的参数如下:PID控制器中的比例系数Kp=10，积分系数KI=80，微分系数 KD=0。模糊PID控制器的控制规则为简单但使用的九条规则。给定转速700 rpm，给定负载转矩初值1 N·m，0.02 s后突变为3 N·m，以此检验系统抗负载扰动的能力，仿真波形如图6所示。

另外抽取图6中部分数据，观察三种控制的细节可得图7。

实验数据如表1所示。稳态误差取 ±2%，即 ±14 rpm。

由表1可发现，ANFIS控制器的不仅调节时间短，而且超调小。并且图7中ANFIS控制曲线达到e小于0.1rpm的时间较其余种控制更短，这说明ANFIS控制器控制的稳态精度比其余二者更好，跟随性更精确。

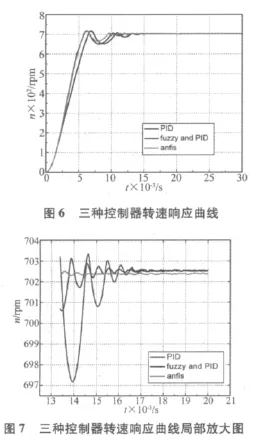
表1 三种控制器控制效果对比

4 结束语

实验可以发现，根据ANFIS设计的速度控制器不仅响应速度比PID控制器好，超调量小。关键是ANFIS在稳态精度方面表现非常好，不仅波动小，而且能很好的跟随指定信号。

更为关键的是自适应神经模糊推理系统(ANFIS)是基于数据的建模方法，该系统中的模糊隶属度函数及模糊规则是通过对大量已知数据的学习得到的，而不是基于经验或直觉任意给定的，这对于那些特性还不被人们所完全了解或者特性非常复杂的系统尤为重要。

［1］杨明，付博，李钊，等.永磁同步电动机矢量控制电压解耦控制研究［J］.电气传动，2010，40(5):24-28.

［2］方斯琛，周波.滑模控制的永磁同步电机伺服系统一体化设计［J］.中国电机工程学报，2009，29(3):96-101.

［3］孙凯，许镇琳，盖廓.基于自抗扰控制器的永磁同步电机位置伺服系统［J］.中国电机工程学报，2007，27(15):43-46.

［4］杨书生，钟宜生.永磁同步电动机伺服系统转速环控制策略综述［J］.电气传动，2006，36(2):3-7.

［5］程飞，过学迅，别辉.电动车用永磁同步电机的双模糊控制研究［J］.中国电机工程学报，2007，27(18):18-27.

［6］Jang J-S R.ANFIS:adaptive-network-based fuzzy inference system［J］.IEEE Transactions on Systems，Man，and Cyber-netics，1993，23(3):665-685.

［7］乔维德.基于神经网络模糊控制的永磁同步电动机直接转矩控制［J］.微特电机，2008(8):36-39.

［8］于侃，高军伟.基于ANFIS中央空调水系统节能控制的仿真研究［J］.青岛理工大学学报，2009(3):122-125.

［9］吴江潦，易灵芝，彭寒梅，等.开关磁阻电机自适应模糊神经网络系统(ANFIS)无位置传感器控制［J］.煤炭学报，2010，35(8):1401-1405.

［10］李国勇.智能预测控制及MATLAB实现(第2版)［M］.电子工业出版社，2010.

［11］DEMUTH H，BEALE M，HAGAN M.Neural network toolbox for use with MATLAB user’s guide［M］.USA，MA:The Math Works Inc，2005.