基于MTS系统的单块试件三轴试验方法研究

汪 斌，周 若，朱杰兵，邬爱清

(长江科学院水利部岩土力学与工程重点实验室，武汉 430010)

1 概述

一般地，室内岩石常规三轴试验采用单一围压轴对称的应力系统，即先对岩石试件施加围压达到某一恒定值(σ2=σ3)，然后增加轴向压力 σ1，直到岩样破坏。一个岩石试件只能得出一对σ1和σ3的数据，无法确定岩石的强度包络线，也不能得到岩石的黏聚力和内摩擦角等参数。水利水电工程岩石试验规程(SL264－2001)中规定岩石三轴试验同一种含水率下岩石试件不得少于5件［1］，然而由于在一些工程中很难取到足够的岩石试件以及试件自身有一定的离散性，试验中会出现试验数据不足以及较为离散现象，因此给试验和数据处理带来了不便。

为了解决该类问题，早在上个世纪80年代，就有国外学者提出了3种不同的三轴压缩试验［2－7］。这些试验都是量测有围压作用下的圆柱形岩石试件的强度，只是试验的轴压和围压加载的应力路径不同，各围压水平下强度峰值点获取的方式不同。J.A.Franklin［3，4］(1970)根据强度包络线产生的不同，提出了3种不同的三轴压缩试验，即:方法I(多块单级加载三轴法)，强度包络线是从几个试验的强度屈服曲线上获得的;方法Ⅱ(单块多级加载三轴法)和方法Ⅲ(单块持续破坏试验)，曲线是通过一个试件的多级加载或连续屈服产生的(如图1所示)。强调了从方法I到方法Ⅲ，单个试件的加载曲线上得到的信息越来越多;而且方法Ⅱ和方法Ⅲ，对试验设备控制性能及试验人员素质的要求也越来越高。但当时由于受到伺服液压机控制性能的限制等方面的原因，该方法仅只是被国际岩石力学学会测试委员会(IRSM)作为建议方法之一，没有对该试验方法的控制方式、分级加载的屈服点的判别及试验结果与传统三轴法的差异性等关键技术问题进行系统研究。

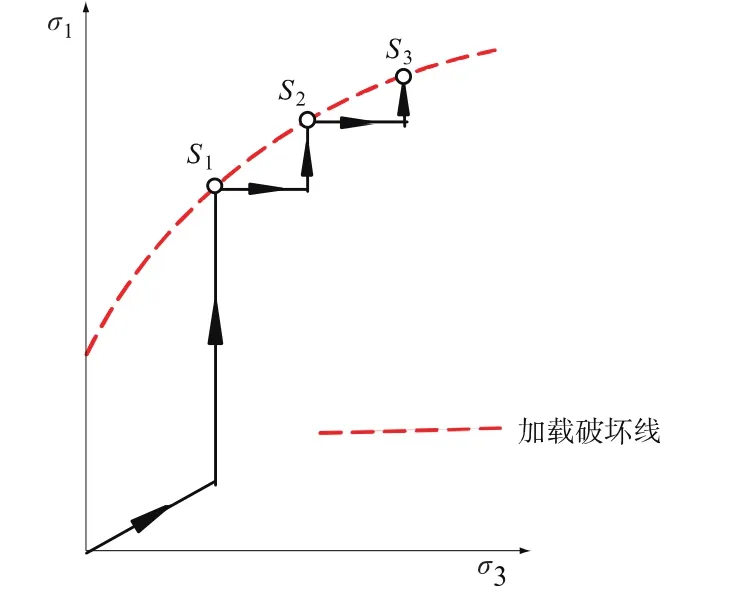
图1 单块多级加载三轴法应力路径示意图Fig.1 Stress path of multiple level triaxial test on single specimen

早期受限于试验机性能，这种单块多级加载的三轴试验技术较为复杂，难以得到推广和应用。近年来，随着电液伺服机和电子计算机技术的成熟和发展，出现了各种性能优良、功能强大的伺服机。国内外一些学者开始致力于该试验方法的一些研究。Kovari K，Tisa A等对Frankin J建议的后2种试验方式进行了分析和探讨［6，7］。国内的一些试验科技人员也对单块多级加载破坏三轴试验法进行了一系列的试验研究［8－12］。国内吴玉山［8］在刚性伺服三轴试验机上通过简单的控制方式，采用单块或少量试件，实现多级围压作用下加载的三轴试验，并且对试验结果进行了分析。苏承东［9］等针对有时试样数量偏少，或离散性较大时会出现围压增大、三轴强度降低的现象，难以确定内摩擦角等参数的问题，基于伺服试验机加载过程的实时控制，对大理岩和砂岩分别提出通过单一岩样确定强度参数的方法。大理岩在围压较高时具有明显的屈服平台，通过对同一试样逐级提高围压的加载方法，就可以得到不同围压下试样的强度，据此可以回归Mohr-Coulomb强度曲线。张磊［10］在刚性伺服三轴试验机上通过对砂岩、泥岩等试验结果进行了分析，认为这种试验方法较适用于中硬以下的岩石;对于硬岩来说，应通过大量的试验找出变换围压时应力与应变曲线切线(割线)模量与弹性段切线(割线)模量的比值来作为试验控制标准。而且认为多级围压下三轴加载试验得到的抗压强度为长期强度，其值是峰值强度的80%左右，那么由长期强度计算得出的黏聚力降低了20%左右，而内摩擦角没有太大变化;因此可以将多级围压下三轴加载试验得到的黏聚力修正为常规三轴加载试验的黏聚力，其修正参考值为 1.0 ～1.25。

纵观国内外研究工作者的研究成果，尽管该三轴方法可以消除岩石离散性及试件数量不足等对试验结果的影响，但是其具体的试验过程及具体试验数据的统计结果有待于进一步研究。在具体工程科学试验中其适用范围、试验结果可靠性及试验技术问题还未得到满意解决。长江科学院岩土力学与工程重点实验室最新引进的MTS815.04岩石力学试验系统(如图2所示)，伺服控制性能优良，变形测试技术先进，为传统的岩石三轴强度试验中的相关问题研究提供了平台。

2 基于MTS815系统的单块试件三轴方法的实现

图2 MTS815.04岩石三轴试验系统及AE系统Fig.2 MTS815.04 triaxial rock mechanical testing system＆AE system

基于MTS815.04岩石力学刚性伺服试验系统的轴向应变及侧向应变控制三轴试验表明:侧向应变控制相对于轴向力或应变控制，岩样的损伤破坏过程是一种可控的、较为稳妥的控制方式，其包络线构成了岩石压缩全过程曲线，而且该曲线可以表达出岩样破坏过程中力学特性的损伤演化信息，对于研究单块三轴法加载控制方式的选取具有深刻的意义［13］。运用该加载控制技术可以较为可靠地实现脆性岩石材料在单块三轴试验方法中的应用。基于MTS815.04岩石力学试验系统的操作平台(如图3所示)，对所有试验步骤采用程序化编程实现，初步建立了一套基于MTS系统的单块样三轴试验程序，实现了实时人机干预、控制和强度屈服点的预判等功能。试验加载和判断流程如图4所示。基于该操作程序，用户只需调用该程序就可以完成自动围压加载、轴向力控制模式选择、干预程序进程等，避免了其他伺服机难以多通道伺服控制的弊端。

图3 MTS815单块样三轴试验程序界面Fig.3 Interface of single specimen triaxial testing by MTS815 system

3 单样三轴试验结果分析及讨论

图4 基于MTS可视化编程平台的单样法流程图Fig.4 Flow chart of single specimen triaxial testing method based on MTS system

为了与常规三轴试验方法得到的岩石三轴强度参数进行比对，选取了同一取样位置同一钻孔的岩样。本次试验采用的是锦屏二级电站交通辅助洞E2-1试验洞(AK08+850)处的T2b地层粗晶大理岩，为了尽量做到所有岩样具有相同的完整性，试验前对所有岩样进行了声波测试并进行了遴选。

采用上节所述的岩样侧面加载控制方式，对每级围压下屈服点进行判别，并实现MTS单样三轴程序化操作。采用了从低、中、高不同围压下单样的强度，围压分别为4，8，12，16，20，30，40，50，60 MPa，得到了整个试验过程曲线及每级围压下强度值，然后经过线性回归后得到了单个岩样的强度参数。本次单样三轴试验试样个数为5个，根据每个试件在不同围压下的强度可以回归得到5组强度参数。岩样编号912-02的单样三轴试验曲线如图5至图11所示。

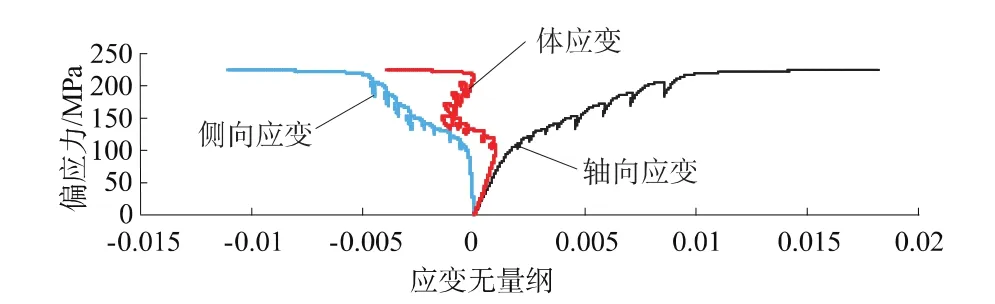
图5 912-02号岩样偏应力-应变曲线Fig.5 Curves of deviatoric stress vs.strain of specimen 912-02

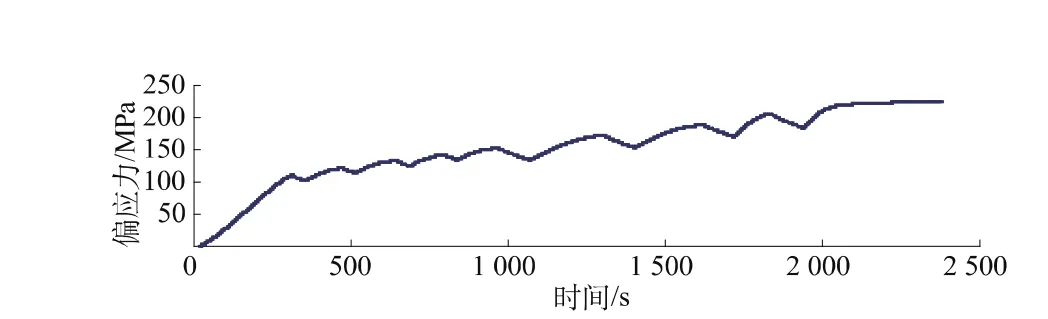
图6 912-02号岩样偏应力-时间曲线Fig.6 Curve of deviatoric stress vs.time of specimen 912-02

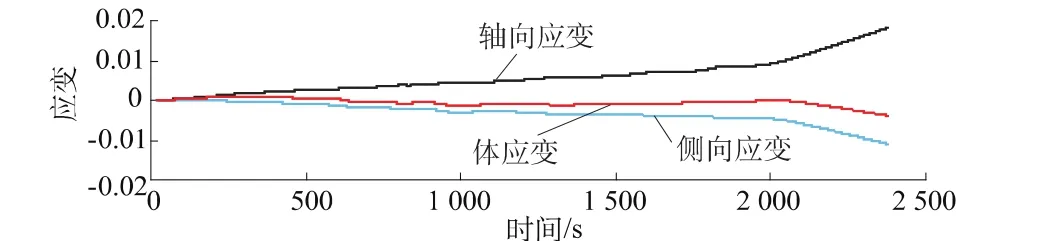
图7 912-02号岩样应变-时间曲线Fig.7 Curves of strains vs.time of specimen 912-02

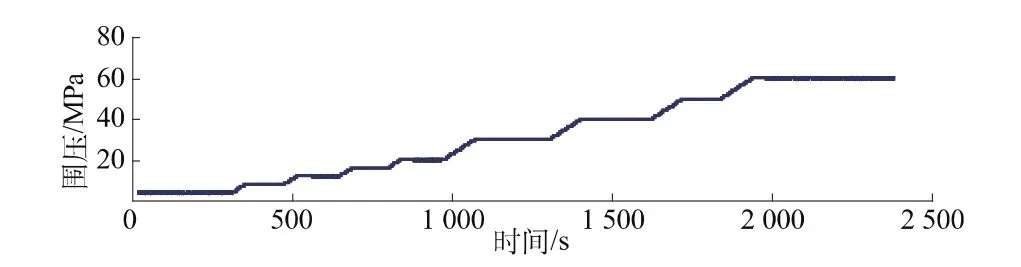
图8 912-02号岩样试验围压-时间曲线Fig.8 Curve of confining pressure vs.time of specimen 912-02

图9 912-02号岩样试验偏应力-围压曲线Fig.9 Curve of deviatoric stress vs.confining pressure of specimen 912-02

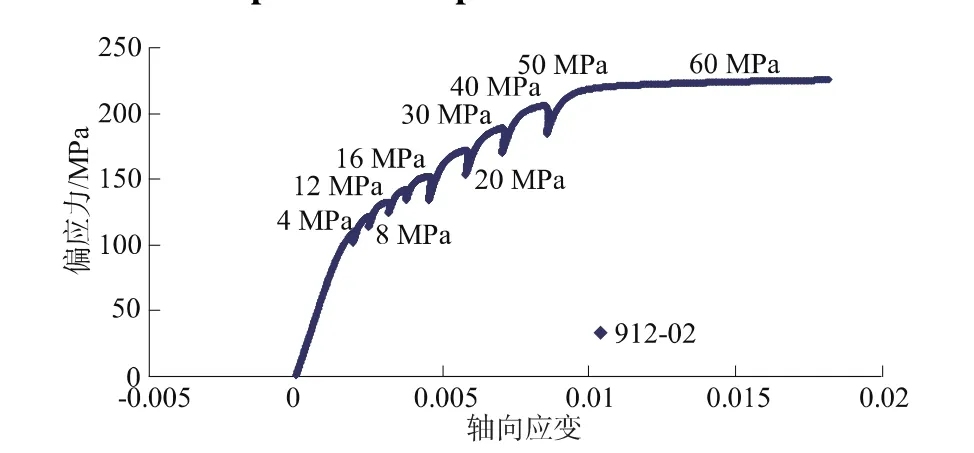
图10 912-02号岩样试验偏应力-应变曲线(不同围压段)Fig.10 Curve of deviatoric stress vs.strain of specimen 912-02(with different confining pressures)

图11 912-02号岩样强度-围压关系曲线Fig.11 Curve of strength vs.confining pressure of specimen 912-02

图5为采用程序化实验过程中采集的轴向应变、侧向应变及体应变随加载过程中偏应力变化曲线。从图10中也可以看到每级围压下体应变拐点变化过程和该级下的强度值。图6为试验过程中偏应力随时间的变化过程，可以看到围压在逐级加载过程中对轴向应力还是有一定的波动影响。图7为轴向应变、侧向应变及体应变随时间变化曲线，在最后一级加载过程中岩石的轴向应变是呈突变式增加，说明岩样强度随变形变化几乎不大，岩样在高围压下呈塑性流动效应。图10至图11为偏应力、轴向总应力随围压变化曲线，因此可以绘出并回归出Mohr-Coulomb强度参数。同时，可以看出采用单样法得到的强度曲线具有很好的相关性，随着围压的增加大理岩强度的非线性也能很好地表现出来。从成果表中还可以看出采用单块样三轴试验成果的离散性远远低于常规三轴试验方法得到的强度参数。

由成果图还可以看到一种现象:常规方法所得强度曲线都比单点屈服三轴试验所得强度曲线高，这种趋势随着应力的增加而增大。这主要是由于在单点屈服三轴试验中随着屈服次数的递增，试件内部微裂纹逐渐增多扩展，虽然围压作用使其部分闭合，但对后一次屈服还是有所影响的。还可以看出:随着屈服次数的增多，试件强度随围压的增加其强度值没有下降，反而还都有增加。这说明经过屈服再对试件增加围压进行试验，此时的试件仍能较好地代表初始性质。这就解除了对该试验方法的“是否每个屈服点都能代表一个试件”的疑虑。但是随着屈服次数的增多这种递增趋势有所减弱而便显出流塑性。如前所述，是由于被压合的微裂纹渐多所致。从此点可以推断:单样三轴试验方法所取的屈服点应该是有限的，当屈服次数达到一定数值时，在强度曲线上将呈现水平发展。

大理岩试件的单样三轴试验成果见表1，将该组所有强度屈服点放在一起进行回归三轴强度参数。从表1中可以看出:无论是在一般应力水平还是在高应力条件下，单样三轴试验得到的强度参数与常规三轴试验结果相比，内摩擦角和黏聚力都有一定比例的减小。在中低围压条件下，前者得到的内摩擦角和黏聚力相对后者分别小 9.57%和 5.56%;而在高围压条件下，前者比后者分别小7.5%。5个试件在围压0～30 MPa范围内的单块样三轴试验强度参数见表2。

表1 常规三轴试验方法与单样三轴试验成果对比表Table 1 Comparison of parameters by conventional triaxial test and single specimen triaxial test

表2 锦屏粗晶大理岩单块岩样三轴试验强度表Table 2 Results of single specimen triaxial test on Jinping marble

同样为了验证大理岩中等脆性硬岩的单样三轴试验成果的可靠性，平行开展了该组相同岩石的常规三轴压缩试验11组，试件个数共55个，试验结果见表3。将其中一组常规三轴试验强度曲线与5个单块试件三轴综合回归强度曲线进行比较。

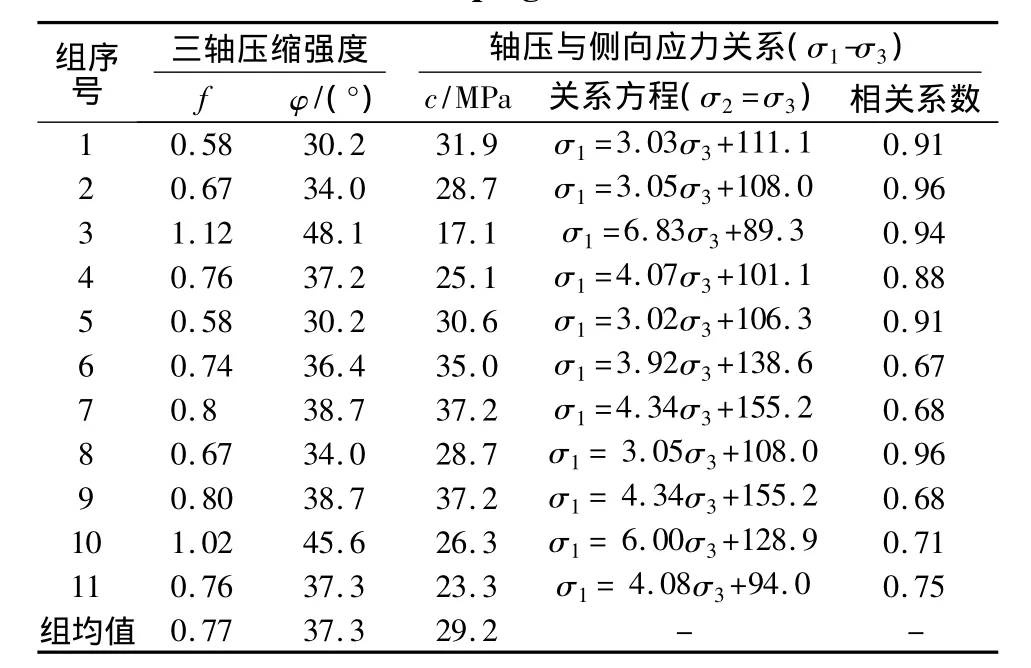
表3 锦屏粗晶大理岩常规三轴强度参数表Table 3 Results of conventional triaxial test on Jinping marble

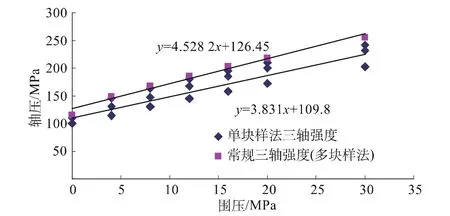
图12 单样三轴与常规三轴强度曲线比较(0～30 MPa围压段 )Fig.12 Comparison of strength curves by single specimen triaxial test and conventional triaxial test(0～30 MPa)

图12和图13分别为围压在0～30 MPa内及0～60MPa内的参数回归与常规多样三轴强度曲线对比。可以看出单样三轴强度总体上较常规三轴试验强度稍小，但是单样法得到更多的强度屈服点，而且没有离散性;结果显示单样法的每个试件强度关系线性拟合相关系数达到0.98，综合拟合相关系数0.91，而常规三轴相关系数在 0.67 ～ 0.96间波动，说明在数据处理和拟合方面，单样三轴法避免了常规三轴法的参数回归相关性差和病态结果等弊端，显示了一定的优越性。从表2和表3中可以看出:11组大理岩常规三轴强度参数内摩角平均值为37.3°，黏聚力平均值为 29.2 MPa;采用5 个相同岩样的单样三轴试验综合回归强度参数内摩角平均值为35.9°，黏聚力平均值为 28.1 MPa，分别较前者减小了3.80%和3.80%;采用组平均统计方式，其强度参数内摩角平均值为34.7°，黏聚力平均值为27.8 MPa，分别较前者减小了 7.00%和 4.80%。

综上所述，单样三轴试验方法中的大理岩试样逐级增加围压的轴向压缩过程中，各级围压下轴向承载能力与不同岩样恒定围压的三轴压缩强度大致相同，其差异在通常的离散范围之内，而且还可以消除不同岩样间差异对试验结果的影响;尤其是当现场取样困难或者试件完整均一性难以达到时，单块试件三轴试验方法的优越性更能体现出来，因此具有一定的工程应用价值。

4 结语

基于MTS815系统程序化试验平台，采用优化加载控制方式、辅以单样法中逐级屈服点预判技术是完全可以对低、中等硬脆性岩石进行单块试件三轴试验的。而且，通过对锦屏大理岩单块岩样三轴试验和常规三轴试验结果进行比较，表明，大理岩常规三轴强度参数内摩角和黏聚力与采单样三轴试验得到强度参数非常接近，可见基于以上技术的单样三轴试验结果是可行的、可靠的。总之，研究成果解决了单块试件三轴试验中的相关关键技术问题，尤其对解决特殊条件下的工程岩石力学参数客观取值方法难题和该三轴试验方法的推广都具有重要的工程应用价值。

［1］SL264－2001，水利水电工程岩石试验规程［S］.(SL264－2001，Specifications for Rock Tests in Water Conservancy and Hydroelectric Engineering［S］.(in Chinese))

［2］HOEK E，BROWN E T.岩石地下工程［M］.连志升，田良灿，王维德，等译.北京:冶金出版社，1986.(HOEK E，BROWN E T.Underground Rock Engineering［M］.Translated by LIAN Zhi-sheng，TIAN Liangcan，WANG Wei-de，et al.Beijing:Metallurgy Industry Publication House，1986.(in Chinese))

［3］FRANKLIN J A，HOEK E.Developments in Triaxial Testing Technique［J］.Rock Mechanics，1970，(2):223－228.

［4］FRANKLIN J A.Suggested Methods for Determining the Strength of Rock Materials in Triaxial Compression［J］.International Journal of Rock Mechanics and Mintra Science，1983，20(6):285－290.

［5］JAEGER J C，COOK N G W.Fundamentals of Rock Mechanics［M］.London:Methuen，1969.

［6］KOVARI K，TISA A.Multiple Failure State and Strain Controlled Triaxial Tests［J］.Rock Mechanics，1975，(7):17－33.(in Chinese))

［7］KOVARI K，TISA A，ATTINGER R O.The Concept of Continuous Failure State:Triaxial Tests［J］.Rock Mechanics and Rock Engineering，1983，16(2):117－131.(in Chinese))

［8］吴玉山，李记鼎.确定岩石强度包络线的新方法——单块法［J］.岩土工程学报，1985，7(2):85－91.(WU Yu-shan，LI Ji-ding.A New Method of Determining Strength Envelope of Rock:Single Specimen Method［J］.Chinese Journal of Geotechnical Engineering，1985，7(2):85－91.(in Chinese))

［9］苏承东，尤明庆.单一试样确定大理岩和砂岩强度参数的方法［J］.岩石力学与工程学报，2004，23(18):3055－3058.(SU Cheng-dong，YOU Ming-qing.Determination Method of Strength Parameters for Sandstone and Marble with One Specimen［J］.Chinese Journal of Rock Mechanics and Engineering，2004，23(18):3055－3058.(in Chinese))

［10］张 磊，王宝学，杨 同.多级围压下岩石三轴试验方法研究［J］.勘察科学技术，2007，(3):7－8.(ZHANG Lei，WANG Bao-xue，YANG Tong.Research of Rock Triaxial Compression Test with Multilevel Confining Pressure［J］.Site Investigation Science and Technology，2007，(3):7－8.(in Chinese))

［11］郭小娟.浅析多级三轴试验加荷方法［J］.江西水利科技，2008，34(1):17－20.(GUO Xiao-juan.Discussion of Loading Method of Multiple-stage Triaxial Test［J］.Jiangxi Hydraulic Science and Technology，2008，34(1):17－20.(in Chinese))

［12］车承国.对一个试样多级加荷三轴剪切试验的探讨［J］.电力勘测设计，2003，3(1):33－37.(CHE Cheng-guo.Discussion of Triaxial Shear Test for Multilevel Adding Load of a Kind of Samples［J］.Electric Power Survey，2003，3(1):33－37.(in Chinese))

［13］张宜虎，汪 斌，景 锋，等.基于生态环境保护的岩体质量评价与锚固研究［R］.武汉:长江科学院，2010.(ZHANG Yi-hu，WANG Bin，JING Feng，et al.Research of Quality Evaluation on Rockmass and Its Anchor Reinforcement Based on Environmental Protection［R］.Wuhan:Yangtze River Scientific Research Institute，2010.(in Chinese))