未确知滤波法和灰色模型在大坝变形预测中的应用

李 波 ，刘明军，张治军

(1.长江科学院a.工程安全与灾害防治研究所;b.水利部水工程安全与病害防治工程技术研究中心，武汉 4 30010;2.中国电力投资集团公司 南 方分公司，广州 5 10130;3.长江勘测规划设计研究院施工设计处，武汉 4 30010)

大坝变形受水位、降雨、气温、地质、时间等多种因素的影响，这些因素之间关系错综复杂，并且具有一定的灰度［1，2］。因此，当大坝变形监测序列较短时，利用灰色模型对大坝变形进行预测，是一种有效的方法。由于人为、系统或环境等原因的影响，大坝变形监测序列中总是存在一定数量的粗差，这必然会影响预测的精度，未确知滤波法可以有效地识别粗差，并对粗差进行修正［3］。因此，本文将未确知滤波和灰色模型相结合，利用未确知滤波法识别并修正大坝变形序列中的粗差，再采用灰色模型对大坝变形进行预测，并结合实例进行分析。

1 未确知滤波法

在大坝变形监测过程中，经常会遇到测值突然增大或减小的情况，这可能是由于人为、系统或环境等因素造成了粗差，也有可能是由于大坝变形发生重大变化导致测值发生异常改变而产生了异常值。从大量的监测数据中正确地分辨粗差和异常值，并将粗差进行修正，准确地反映大坝的工作状态显得非常重要。未确知滤波法能够很好地分辨粗差和异常值，在一些领域已得到应用［4，5］。

1.1 未确知滤波法原理

在大坝安全监测中，变形监测量的某个监测序列为

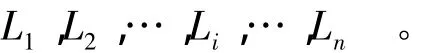
定义一个未确知有理数为

其中φ(x)是可信度分布密度函数。

通过对粗差和异常值进行分析，不难看出，若Li是粗差，Li是孤立的，则在 Li的某个邻域内 Lj(1≤j≤n，j≠i)个数为零，因此，可信度分布密度函数φ(x)可作如下定义:

式(2)中ξi表示Lj在以λ为半径的Li的领域中的个数。

通过式(2)定义可信度分布密度函数φ(x)，如果Lj在以λ为半径的Li的领域中的个数越多，可以认为Lj为非粗差的可能性就越大;相反地，如果Lj在以λ为半径的Li的领域中的个数越少，甚至只有1次，则认为Lj为粗差的可能性就越大。未确知滤波法就是基于这个原理对监测系列中的粗差和异常值进行区分，从而达到去噪的目的。

进一步计算未确知滤波法的数学期望，可以修正粗差。未确知滤波法的数学期望如下所示:

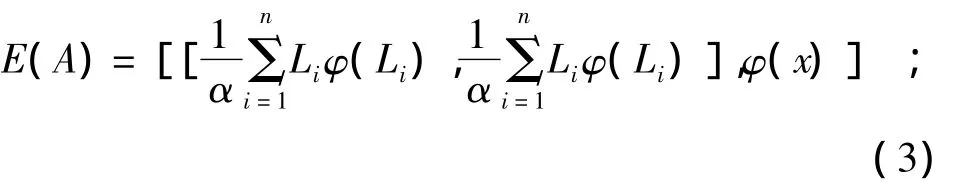
由于式(4)满足

故式(3)可以简化为

可信度决定粗差的分辨，可信度又与ξi相关，ξi又完全由邻域半径λ的大小决定，如果λ取值过大，则有可能将粗差包含在内，不能识别粗差;反之，如果λ取值过小，则会把正常数据中的偏大值误认为粗差。因此，λ的取值直接影响未确知滤波的最终结果。参考传统粗差分辨方法中的2或3倍中误差法则，λ取2倍差值方差为

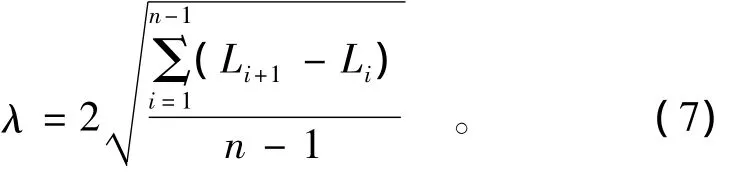
1.2 改进的未确知滤波法

大坝安全变形监测的测值序列中，粗差的可信度和ξi应该为零，但在现实的情况很难这么理想，大坝测值序列较长时，部分粗差和正常的测值在某段序列中非常接近，使粗差难以识别。为此，可以把测值序列进行分段处理［4］，每段测值含有k+1个监测值，分别对每段监测值进行滤波处理，可以重新定义可信度分布密度函数φ(x)为

式中:ξi表示半径为λ的Li的领域V中包含Lj的个数;Lj为相邻Li最近的k个监测值(i≠j)。

分段后对应的未确知期望也发生变化，在含有k+1监测值求未确知数学期望为

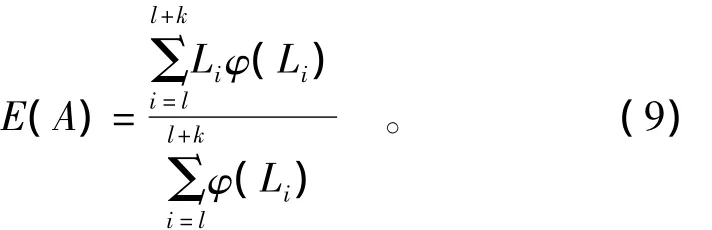
改进的未确知滤波法处理粗差流程图如图1所示。改进的未确知滤波法处理粗差的主要步骤如下:

(1)选取原始的监测序列 Li(i=1，2，…，n)，确定 m 的取值范围［2，mmax］，取 m=2，j=1;

(2)由式(7)计算出监测序列的邻域半径λj;

(3)根据:邻域上限=监测值+λi、邻域下限=监测值－λj，计算各监测值邻域的上下限;

(4)滤波数据段为包括Li及其相邻最近的k个测值在内的k+1个测值，统计出落在Li相应邻域内的其它监测值个数ξi;

(5)根据式(8)算出Li的可信度;

(6)重复步骤(3)至步骤(5)，算出每个监测值的ξi和可信度，判断Li是否为粗差;

(7)剔除粗差，计算剩余监测值的邻域半径λj+1;

(8)如果 λj+1= λj，则 λm=λj，进入步骤(9)，否则，j=j+1，重复步骤(2)至步骤(7);

(9)当 m=mmax时，进入步骤(10)，否则，取m=m+2，重复步骤(2)至步骤(8);

(10)取邻域半径λm中的最小值λmin作为滤波计算的最终λ值;

(11)在λmin所处的状态下，根据式(9)计算出每个监测值的未确知数学期望。

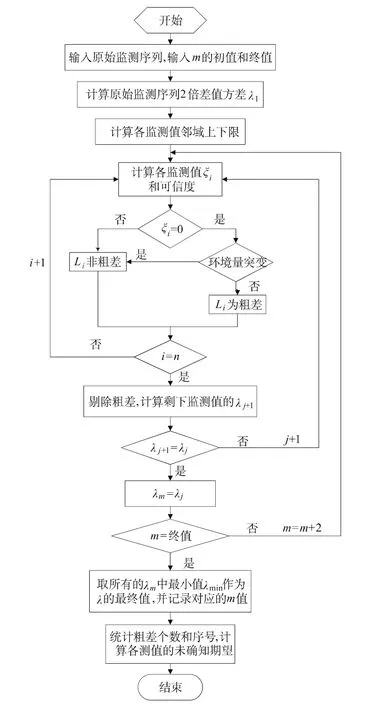
图1 改进的未确知滤波法处理流程图Fig.1 Flow chart of processing the gross error by improved unascertained filtering method

2 等维新息灰色模型

上世纪80年代，我国学者邓聚龙教授建立了灰色系统理论。将已知的数据序列按照某种规则构成动态或非动态的白色模块，再按照某种解法来求解未来的灰色模型。

灰色系统理论中常用的是微分方程所描述的动态方程。其中GM(1，1)表示一阶、单个变量的微分方程模型［6］。其具体形式为

用序列 x0表示 n个监测值 x01，x02，…，x0n，对 x0进行累加求和，得到新的序列x1，其一般元素x1i(上标1表示新序列，下标表示新序列中的第i个监测值)的计算公式为

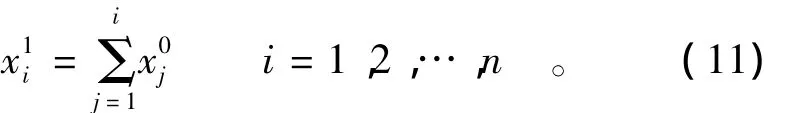
则对新的序列x1，有如下形式的方程，即

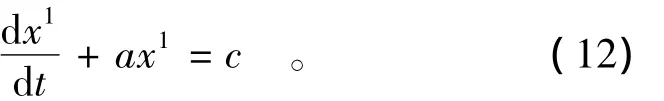
用最小二乘法求解，得到2待定参数a和c的估计值计算公式为

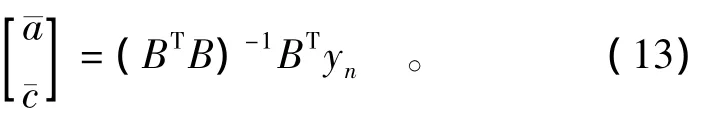
式中:¯a和¯c分别为a和c的估计值;

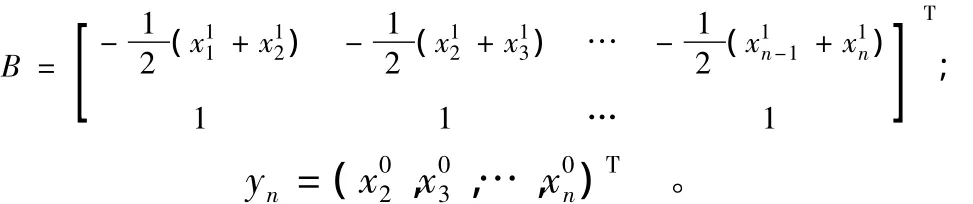
将利用式(13)估计好的2参数¯a和¯c代入方程式(12)，并求解该微分方程，得到GM(1，1)预测模型的表达式为

对上式进行还原得到原始测值序列拟合和预测值，则有

等维新息模型是采取新信息替代旧信息的方式建模，又称为新陈代谢模型。

3 实例分析

以某水电站坝顶水平位移的引张线测点EX9为研究对象，选取该测点2006年6月16日至2006年7月6日共20个自动化测值，如表1所示。利用未确知滤波进行粗差分析，其结果如表2所示。

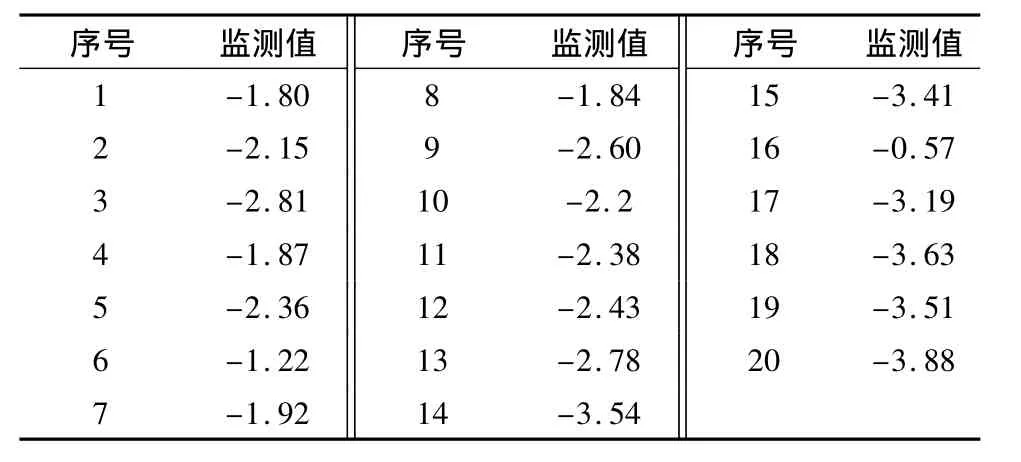
表1 EX9测点2006年6月16日至7月6日的监测值序列Table 1 Monitoring values at point EX9 from June 16 to July 06 in 2006mm

表2 不同m值的改进未确知滤波法识别粗差结果Table 2 The results of detecting gross error by improved unascertained filtering with different m values

从表2的计算结果可知，m取2，4，6时，λ最终收敛至1.09，识别到1个粗差;m取8～18时，最终收敛至 2.06，没有识别到粗差。考虑到 1.09＜2.06，在m取8～18时可能出现了粗差遮蔽的情况。同时，结合实测环境变量发现，m取2，4，6时识别出的1个粗差的监测时刻前后，上游水位和气温均没有出现异常现象，因此，m取2，4，6时得到的结果合理，最终识别出的粗差序号为16。通过式(9)得到各粗差的修正值分别为－3.30 mm。

在未确知滤波识别粗差，并对粗差进行修正的基础上，再利用等维新息灰色模型对修正后的水平位移进行预测。选取前16个测值建立灰色模型，对后4个测值进行预测。建立的灰色模型中2个参数a 和 c的估计值分别为－0.054 9和－1.667 5，预测结果见表3所示。为了进行比较，对原始水平位移测值进行上述相同的预测，得到的预测结果见表3所示。由表3可知，修正后的水平位移灰色模型预测精度明显的高于修正前，因此，本文提出的方法具有较高的实用价值。

表3 修正前后水平位移灰色模型预测结果Table 3 Prediction of horizontal displacement by grey model before and after the correction mm

4 结论

本文通过未确知滤波和灰色模型对大坝变形监测数据进行了分析和预测，得到了以下结论:

(1)改进的未确知滤波法可以有效地区分粗差和异常值，并通过对粗差进行修正，减少了监测误差和保证了测值序列的完整性;等维新息灰色模型可以反映监测序列的动态变化情况，更能反映大坝变形的时间情况。

(2)充分利用未确知滤波法和灰色模型的优点，将2种方法有机地结合，应用大坝变形预测中。实例分析表明，基于未确知滤波法的灰色模型能显著地提高大坝变形预测精度，具有较高的工程实用价值。

［1］吴中如.水工建筑物安全监控理论及其应用［M］.高等教育出版社，2003.(WU Zhong-ru.Theory of Safety Monitoring of Hydraulic Structures and Its Application［M］.Higher Education Press，2003.(in Chinese))

［2］顾冲时，吴中如.大坝与坝基安全监控理论和方法及其应用［M］.南京:河海大学出版社，2006.(GU Chong-shi，WU Zhong-ru.Theory of Dam and Foundation Safety Monitoring and Its Application［M］.Nanjing:Hohai University Press，2006.(in Chinese))

［3］冯小磊，华锡生，黄红女.观测值序列的粗差探测方法［J］.水电自动化与大坝监测，2006，30(3):56－59.(FENG Xiao-lei，HUA Xi-sheng，HUANG Hong-nv.Gross-error Detection for Observation Data Series［J］.Hydropower Automation and Dam Monitoring，2006，30(3):56－59.(in Chinese))

［4］黄红女，华锡生，宋小刚.土石坝监测数据的未确知滤波［J］.长江科学院院报，2006，23(3):32－35.(HUANG Hong-nv，HUA Xi-sheng，SONG Xiao-gang.Unascertained Filtering Method for Monitoring Data of Earth Rock-fill Dams［J］.Journal of Yangtze River Scientific Research Institute，2006，23(3):32－35.(in Chinese))

［5］张 锋，郝金明，郭 磊，等.基于未确知有理数的VRS综合误差粗差探测与修复［J］.测绘科学技术学报，2009，26(6):403－406.(ZHANG Feng，HAO Jinming，GUO Lei，et al.Gross Error Detection and Reparation for VRS Synthetical Error Based on Unascertained Rational［J］.Journal of Geomatics Science and Technology，2009，26(6):403－406.(in Chinese))

［6］程启明，程尹曼，汪明媚，等.基于灰色预测的无模型控制在球磨机负荷控制中的仿真研究［J］.仪器仪表学报，2011，32(1):87－92.(CHENG Qi-ming，CHENG Yin-man，WANG Ming-mei，et al.Simulation Study on Model-Free Adaptive Control Based on Grey Prediction in Ball Mill Load Control［J］.Chinese Journal of Scientific Instrument，2011，32(1):87－92.(in Chinese ))