基于变步长滞环比较法的MPPT算法研究

徐高晶 陈 婷 徐 韬

（1.国网电力科学研究院南京南瑞智源电气技术有限公司，南京 210009；2.南京工业大学信息学院，南京 210009）

随着社会的发展，能源和环境成为人们面对的紧要问题。太阳能作为一种广泛分布的清洁可再生能源有很好的应用前景[1]，其中太阳能光伏发电技术得到了大量研究和应用，在光伏发电系统中，光伏电池的利用率除了与光伏电池的内部特性有关外，还受使用环境如辐照度、负载和温度等因素的影响。在不同的外部环境下，光伏电池可运行在不同且惟一的最大功率点（Maximun Power Point，MPP）上。因此对光伏发电系统来说，应当寻求光伏电池的最优工作状态，以最大限度的将光能转化为电能[2]。

目前常用的实现MPPT的方法有导纳增量法、扰动观测法等。导纳增量法是利用光伏电池在MPP处输出功率对电压的导纳为零来跟踪MPP，该方法控制效果好，控制稳定度较高，但是控制算法复杂，对采样的精确度要求很高[3]。扰动观测法是根据光伏电池的输出功率的变化趋势来扰动光伏电池的输出电压，使光伏电池最终工作于最大功率点。但振荡和误判问题的存在，使系统不能准确地跟踪到最大功率点，造成了能量损失[2]。

综上所述，以传统扰动观测法为基础提出的变步长滞环比较法不但在克服最大功率点跟踪过程中的振荡和误判方面均有较好的性能，且能兼顾到速度和精度的要求，更加准确地跟踪光伏电池的最大功率点，从而提高光伏系统的发电效率。

1 光伏电池特性分析

1.1 光伏电池的等效电路

光伏电池实际上就是一个大面积平面二极管，可以用图 1的单二极管等效电路来描述。图中 RL是光伏电池的外接负载，负载电压（亦即光伏电池的输出电压）为UL，负载电流为IL。

由图1，可得负载电流IL为

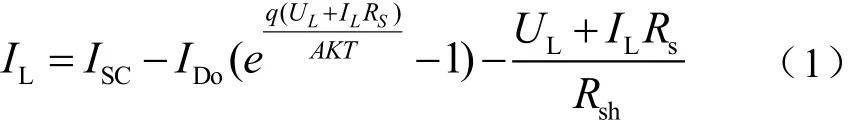
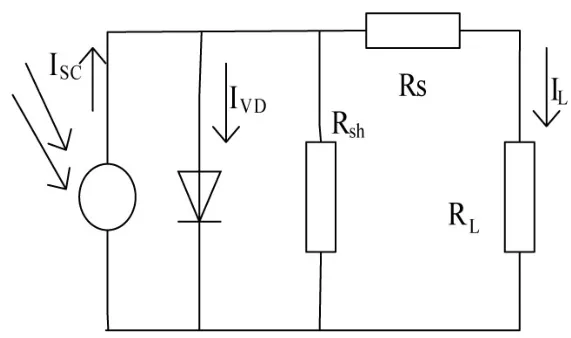
图1 光伏电池的等效电路

式中，ISC为光子在光伏电池中激发的电流；IDO为光伏电池在无光照时的饱和电流；q为电子的电荷，1.6×10-19C；RS为串联电阻（由电池的体电阻、表面电阻、电极导体电阻、电极与硅表面间电阻所组成）；A为一个常数因子（正偏电压大时A值为1）；K为玻尔兹曼常数，1.38×10-23J/K；Rsh为并联电阻（有硅片的边缘不清洁或体内的缺陷引起的）。

1.2 光伏电池数学模型及输出特性

一般光伏电池，串联电阻 Rs很小，并联电阻Rsh很大，在进行理想电路计算时可忽略不计，理想光伏电池的特性为

设在参考条件下，Isc为其短路电流，Uoc为其开路电压，Im，Um为最大功率点电流和电压，则当光伏阵列的电压为Vpv时，其对应的电流为Ipv，根据光电池厂提供的 Im，Um，Isc，Uoc等参数就可以确定该光伏电池的输出特性，但是由于厂商提供的这些参数一般是在标准温度（Tref=25℃）和标准日照功率（Sref=1000W/m2）下的测试结果，在实际应用中还需要进行补偿[4]，可以根据得到[2]

基于式（3），我们使用Matlab搭建了光伏电池的仿真模型如图 2所示。参数为：电流变化温度系数a=0.015Amps/℃，电压变化温度系数 b=0.700V/℃，Isc=5.45A，Uoc=22.2V，Im=4.95A，Um=17.2V。

图2 光伏阵列Matlab仿真模块内部结构

封装后的PV模块如图3所示。

图3 光伏阵列Matlab仿真模型封装

模拟光照强度从 1000W/m2递变到200W/m2时系统的输出性能，如图4所示。

由图 4可知，光伏器件输出功率 Ppv与输出电压Upv，电流Ipv呈非线性关系，在不同的环境即温度，日照强度下，光伏器件存在唯一最大输出功率点。当光伏器件置于室外环境时，由于外部环境不断改变光伏器件最大功率也随之改变。

图4 给定光照曲线下光伏阵列的输出特性

2 变步长滞环比较法实现最大功率点跟踪技术

工作点到达最大功率点附近时，对于定步长的扰动方式，会出现工作点跨过最大功率点的情形，但改变扰动方向后，工作点电压与最大功率点电压的差值还是小于步长，无法达到最大功率点，这种由于扰动步长一定所导致的工作点在最大功率点两侧往复运动的情形，就是扰动观测法的振荡现象。当外界环境发生变化时，光伏电池的输出功率特性曲线也发生变化，会出现一段时间内工作点序列位于不同的Ppv-Upv特性曲线上的情形。此时对于不同的 Ppv-Upv特性曲线上的工作点继续使用针对于固定特性曲线的判据，就会出现扰动方向与实际功率变化趋势相反的情形，就是扰动观测法的误判现象。

2.1 变步长滞环比较法原理

从控制角度而言，抑制振荡可以采用具有非线性特性的滞环控制策略，针对光伏电池的 Ppv-Upv特性，其滞环控制环节如图5所示。

图5 滞环技术示意图

当功率在所设的滞环内出现波动时，光伏电池的工作点电压保持不变，只有当功率的波动量超出所设的滞环时，才按照一定的规律改变工作点电压。可见滞环的引入，可以有效地抑制扰动观测法的振荡现象。实际上可以将误判看成是外部环境发生变化时的一种动态的振荡过程，因此该方法也可以克服扰动观测法的误判现象。

2.2 系统功能的实现

虽然滞环比较法可以较大程度地避免振荡和误判现象，但如果步长过大，工作点可能会停在离最大功率点较远的区域，如果步长过小，在新一轮开始搜索时，工作点会在远离最大功率点区域内长时间地搜索，因此速度和精度的矛盾依然存在，采用变步长的滞环比较法便可以解决这一矛盾，具体流程图如图6。

图6 变步长滞环比较法流程图

其原理如下：

在太阳能电池P-V特性曲线顶点附近从左至右依次取C，A，B三点，设变化标志m，扰动量为n，PC，PA，PB对应于 A，B，C 三点的功率，规定当 PB≥PA时，m=1，PB＜PA时，m=-1；当 PA≥PC时，m=1，当PA＜PC时，m=-1。这样根据m的值就可以做出扰动方向的判断。

（1）m=2，PB≥PA&PA≥PC，增加扰动量，增加步长，令n=2n；

（2）m=0，PC＜PA& PB＞PA，达到最大点；

（3）m=-2，PB＜PA&PA＜PC，减小扰动量减小步长，令n=n/2。

3 实验结果分析

为了验证所提出方法的正确性，把MPPT控制系统串入Boost变换器电路中，在Matlab/Simulink仿真软件下搭建的仿真模型中，编写 S函数作为MPPT的控制模块，对光伏电池的最大功率点进行跟踪，MPPT的仿真模型如图7所示。为了形成对比，对采用扰动观测法和变步长的滞环比较法MPPT控制方法进行了仿真。

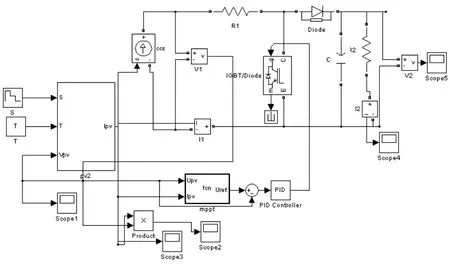
图7 光伏并网Matlab仿真模型

根据图7的光伏系统仿真模型，分别在MPPT模块应用扰动观察法和变步长的滞环比较法对外界条件变化后的某一瞬间进行仿真，如图 8，图 9所示。由图8可以看出扰动观察法在0.004s左右即可达到最大功率点，波形在往后的范围内处于震荡较明显的情况。而图9的变滞环比较法在0.00025s处即已达到最大功率点且波动比较小，说明变步长的滞环比较法的确在原来扰动观察法的基础上无论是从精度还是速度方面都有了一定程度的改进，从而提高了光伏系统的发电效率。

图8 基于扰动观察法的光伏电池输出功率仿真波形图

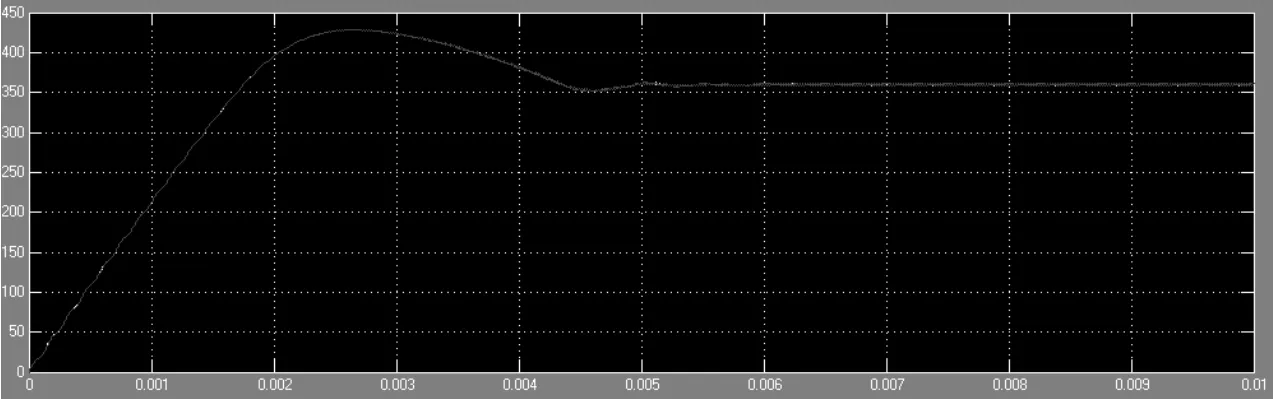
图9 基于变步长的滞环比较法的光伏电池输出功率仿真波形图

4 结论

本文对光伏电池特性进行了详细的分析，针对光伏系统的最大功率点跟踪问题进行了研究，提出了基于扰动观察法的变步长滞环比较法。变步长的滞环比较法的最大优点是通过双向扰动确认的方法来保证扰动观测法的动作可靠性，以避免误判的发生，同时在搜索过程中不断调整搜索的步长，也有效的抑制了最大功率点附近的振荡。仿真结果表明，该算法具有很好的跟踪速度和精度，是一种比较理想的控制方法，但是稳定性方面还需要改进。

[1]朱铭炼,李臣松,陈新等.一种应用与官府系统 MPPT的变步长扰动观察法[J].电力电子技术,2010,44(1):20-22.

[2]张兴,曹仁贤.太阳能光伏并网发电及其逆变控制[M].北京:机械工业出版社,2011.1.

[3]张超,何湘宁. 短路电流结合扰动观察法在光伏发电最大功率点跟踪控制中的应用[J].中国电机工程学报,2006,26(20):98-102.

[4]张建坡,张红艳,王涛等.光伏系统中最大功率跟踪算法仿真研究[J].计算机仿真,2010,1(27):266-269.

[5]张超,何湘宁,赵德安.光伏发电系统变步长MPPT控制策略研究[J].电力电子技术,2009,10(43):47-49.