基于Kriging模型的挡风墙优化设计

黄尊地，梁习锋，钟睦

(中南大学 交通运输工程学院，轨道交通安全教育部重点实验室，湖南 长沙，410075)

兰新(甘肃兰州—新疆乌鲁木齐)铁路穿越新疆大风戈壁地区，自然条件十分恶劣，尤其是大风给列车运行安全造成的影响更为严重。在强侧风作用下，列车空气动力性能恶化，不仅列车空气阻力、升力、横向力迅速增加，还影响列车的横向稳定性，严重时将导致列车倾覆[1]。对于一些特殊的风环境如高路堤等，列车的绕流流场改变更为突出，空气动力显著增大，导致列车翻车的可能性大大增加。为使列车安全通过风区，必须在兰新线50 km风区铁路沿线迎风一侧修建挡风墙。挡风墙的修建存在路堤高度和挡风墙高度的搭配问题。若挡风墙高度过低，则强侧风将直接吹向列车；若挡风墙高度过高，则将在列车和挡风墙之间形成强大的涡流，使车辆受到倾覆力矩剧增。因此，挡风墙过高或过低均会对列车产生较大的倾覆力矩。刘凤华等[2-6]研究了二维模型下路堤、挡风墙和倾覆力矩三者之间的关系，在此，本文作者充分考虑到机车、风挡以及转向架对整列车流场的影响，用三维列车模型来研究其中的变化规律。本文采用Kriging近似模型[7-9]，用较少的样本点，得到不同路堤和挡风墙高度下倾覆力矩的变化规律，应用序列二次规划优化算法，不仅可以求出最优挡风墙的高度，而且节省了时间，提高了效率。

1 挡风墙优化设计方法

对问题进行全面分析后，首先要考虑的是设计的变量。确定变量后，进行试验设计，安排计算工况；选择CFD软件计算所需目标值；用计算得到的目标值建立 Kriging近似模型，进而得到目标值和各参数之间的变化规律。

用建立的 Kriging模型，结合目标函数、约束条件以及优化算法进行优化分析，求得变量的最优解。挡风墙优化设计步骤如图1所示。

图1 挡风墙优化流程图Fig.1 Flow chart of wind-break wall optimization

1.1 确定优化变量

优化变量为路堤高度x1和挡风墙高度x2，计算设置棚车的车速为 80 km/h，风速为百里风区内有记录的最大风速46 m/s，线间距和道床厚度等其他参数均为兰新线上的实际尺寸。

1.2 试验设计

建立 Kriging近似模型的前提是有一定数量的样本数据。在整个设计空间中选取有限数量的样本，要求尽可能全面反映设计空间特性，应选用试验设计的方法。试验设计方法有很多，如全因子设计、中心组合设计、拉丁超立方设计等等。在各种设计方法中，最优拉丁超立方试验设计是在拉丁试验设计基础上优化而成，是一种更高效的试验设计技术，在设计空间内均匀、随机、正交采样，能够用比较少的样本点获得大量的模型信息[10]。

1.3 数值计算

实际运行的棚车编组总长达到几百米，由于中间车辆截面形状不变，当气流流过车头一定距离后，绕流边界层的结构已趋于稳定，车辆气动力变化也趋于稳定。因此，计算模型选择4车编组，即DF11机车加3节棚车，挡风墙选择比较普遍的加筋对拉式，线路为靠近挡风墙的一线。

FLUENT稳态计算中，由于车速和风速都小于马赫数 0.3，所以，流体设置为不可压气体[11-12]。不可压缩流体流场的数值采用SIMPLEC方法求解[13-14]。列车为细长物体，其边界层大多为湍流边界层，因此，必须模拟湍流。本文应用κε-双方程湍流模型，选择精度比较高的 QUICK格式[15]，网格采用四面体非结构网格。

1.4 Kringing模型

常用的近似模型包括多项式函数、多元自适应回归、径向基函数、Kriging模型、神经网络等等，但在解决非线性程度较高的问题时，采用 Kriging近似模型比较容易取得理想的拟合效果。Kriging近似模型的原理见文献[16]。

1.5 目标函数和约束条件

在线路上行驶的棚车，最危险的时刻应该是头车、中车和尾车三者中倾覆力矩绝对值出现最大的时刻。不同路堤和挡风墙下的最大值可构成一列数组，在数组最小值点处，路堤和挡风墙高度的搭配应该是最优的，由此构造目标函数为：

式中：fx=max{|f1|, |f2|, |f3|}；f1为头车倾覆力矩；f2为中车倾覆力矩；f3为尾车倾覆力矩。约束条件为：

式中：x1为路堤高度；x2为挡风墙高度。

1.6 序列二次规划算法

优化分析采用序列二次规划算法。其基本思想如下：在某个近似解处，将原非线性规划问题简化为一个二次规划问题，求取最优解，若有，则认为是原非线性规划问题的最优解，否则，用近似解代替构成一个新的二次规划问题，继续迭代。

在本文中，式(1)为序列二次算法的目标最小化，路堤高度在其取值范围内随机取 x1=，具有约束 1≤x2≤3， x =2。序列二次规划算法通过将原问题转化为一系列二次规划子问题的求解来获得原问题的最优解，对拉格朗日函数取二次近似，从而提高二次规划子问题的近似程度。变化灵敏性越高；在所有路堤高度下，棚车的倾覆力矩随优化带上面挡风墙高度的变化趋势比较平缓，而随优化带下面的挡风墙高度变化趋势较大。

优化算法得到最优挡风墙的高度如表1所示，表1中同时列出了数值计算验证的最优挡风墙高度的范围。通过对比分析可知：两者是一致的。

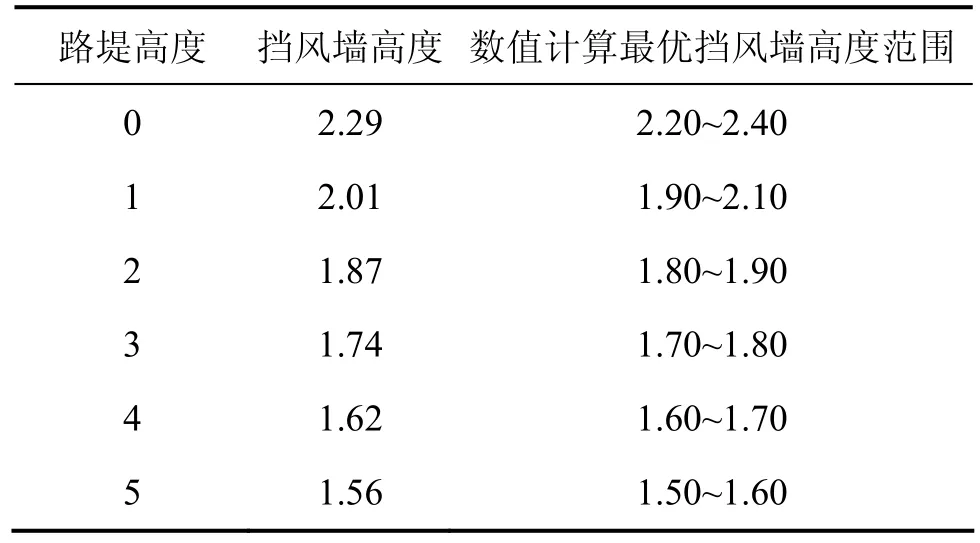
表1 最优挡风墙高度Table 1 Height of the best wind wall m

2 挡风墙优化结果分析

基于以上挡风墙优化设计的方法，综合考虑3节棚车的气动性能，得出其倾覆力矩的绝对值随路堤和挡风墙高度的变化规律，并求出不同路堤下挡风墙的最优高度。以下提到的倾覆力矩均指由式(1)计算后的三节棚车统一的倾覆力矩。

在任意路堤下，3节棚车的倾覆力矩不可能同时取0 N·m，这样倾覆力矩绝对值的最大值数列中，最小值不可能是0 N·m，而是一个较小的正数。把优化变量和得到的最低值描绘成等高线图，可以容易地反映出约束条件下最低值在路堤和挡风墙高度围成的二维平面内的变化规律，如图2所示。

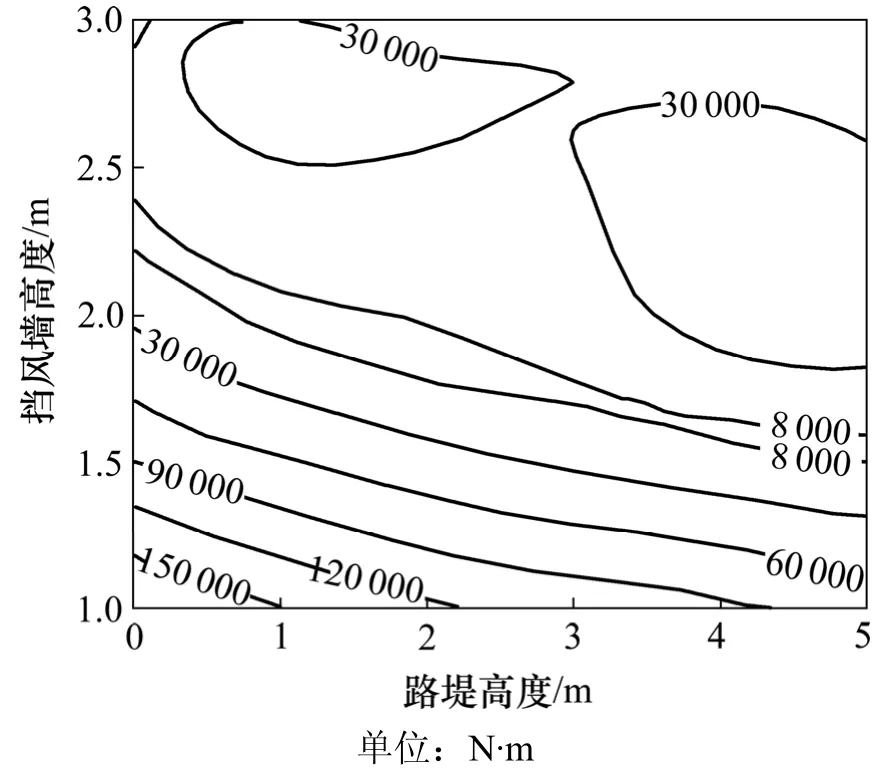
图2 倾覆力矩的等高线图Fig.2 Contour line of overturn moment

在图2所示的等高线中，在2条倾覆力矩较小的范围线内，是路堤和挡风墙组合的最优组合范围，即优化带；当路堤高度较低时，优化带较宽；当路堤越高时，优化带也越窄，并且倾覆力矩对挡风墙高度的

从表1可见：路堤高度不同，挡风墙高度不同；当路堤高度逐渐增大时，棚车最优的挡风墙高度不断减小，减小的幅度变小；在最优挡风墙高度下，列车行驶时仍有一定的倾覆力矩，所以，在大风环境下，列车应减速以便安全通过风区。基于以上最优挡风墙高度和路堤高度的变化规律，可以拟合成1条指数函数曲线，如图3所示。

图3 最优挡风墙高度和路堤关系图Fig.3 Relationship between height of the best wind wall and embankment

拟合曲线的公式为：

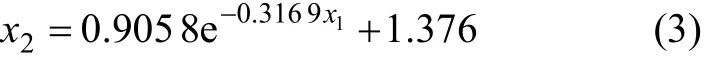
式中：x1为路堤高度；x2为最优挡风墙的高度；残差平方和为0.001 229；相关系数为0.996 7，曲线拟合的程度非常好。通过式(3)，可以得到0～5 m内任意路堤下最优挡风墙的高度。

3 结论

(1) Kriging插值模型和最优拉丁超立方试验设计可以用于挡风墙的优化设计，与大量工况的数值计算结果比较，Kriging插值模型有更强的预测能力，大大减少了计算工况的次数，提高了效率。

(2) 当路堤高度较低时，倾覆力矩的优化带较宽；若路堤越高，则优化带也越窄，并且倾覆力矩对挡风墙高度的变化灵敏性越高；在所有路堤高度下，棚车的倾覆力矩随优化带上面挡风墙高度的变化趋势比较平缓，而随优化带下面挡风墙高度的变化趋势较大。

(3) 路堤高度越高，则最优挡风墙的高度不断减小，但减小的幅度越来越小；当路堤高度为0～5 m时，可以得到任意路堤高度下的最优挡风墙高度。

[1] 田红旗. 列车空气动力学[M]. 北京: 中国铁道出版社, 2007:40-43, 110-117.TIAN Hong-qi. Train aerodynamics[M]. Beijing: China Railway Press, 2007: 40-43, 110-117.

[2] 刘凤华. 加筋土式挡风墙优化研究[J]. 铁道工程学报,2006(1): 96-99.LIU Feng-hua. Study on the optimization of wind-break wall of the reinforced concrete shaped type[J]. Journal of Railway Engineering Society, 2006(1): 96-99.

[3] 刘凤华. 不同类型挡风墙对列车运行安全防护效果的影响[J].中南大学学报: 自然科学版, 2006, 37(1): 176-182.LIU Feng-hua. Wind-proof effect of different kinds of wind-break walls on the security of t rains[J]. Journal of Central South University: Science and Technology, 2006, 37(1):176-182.

[4] 姜翠香, 梁习锋. 挡风墙高度和设置位置对车辆气动性能的影响[J]. 中国铁道科学, 2006, 27(2): 66-70.JIANG Cui-xiang, LIANG Xi-feng. Effect of the vehicle aerodynamic performance caused by the height and position of wind-break wall[J]. China Railway Science, 2006, 27(2): 66-70.

[5] 王厚雄, 王蜀东, 高注, 等. 防风工程对风特性及铁道车辆横风气动特性的影响[J]. 空气动力学学报, 1990, 8(4): 430-435.WANG Hou-xiong, WANG Shu-dong, GAO Zhu, et al. Effects of wind-break engineering on wind characteristics and lateral aerodynamic characteristics on railway cars[J]. Acta Aerodynamica Sinica, 1990, 8(4): 430-435.

[6] 王厚雄, 高注, 王蜀东, 等. 挡风墙高度的研究[J]. 中国铁道科学, 1990, 11(1): 14-22.WANG Hou-xiong, GAO Zhu, WANG Shu-dong, et al. Study on the height of wind break wall[J]. China Railway Science, 1990,11(1): 14-22.

[7] 王晓锋, 席光. 基于Kriging模型的翼型气动性能优化设计[J].航空学报, 2005, 26(5): 545-549.WANG Xiao-feng, XI Guang. Aerodynamic optimization design for airfoil based on Kriging model[J]. Acta Aeronautica et Astronautica Sinica, 2005, 26(5): 545-549.

[8] 于向军, 张利辉, 李春然, 等. 克里金模型及其在全局优化设计中的应用[J]. 中国工程机械学报, 2006, 4(3): 259-261.YU Xiang-jun, ZHANG Li-hui, LI Chun-ran, et al. Applying Kriging model for global design optimization[J]. Chinese Journal of Construction Machinery, 2006, 4(3): 259-261.

[9] 丁继锋, 李为吉, 张勇, 等. 基于响应面的翼型稳健设计研究[J]. 空气动力学学报, 2007, 25(1): 19-22.DING Ji-feng, LI Wei-ji, ZHANG Yong, et al. Robust airfoil optimization based on response surface method[J]. Acta Aerodynamica Sinica, 2007, 25(1): 19-22.

[10] Montgomery D C. Design and analysis of experiments[M]. New York: John Wiley & Sons, 1997: 118-121.

[11] 费祥麟, 胡庆康. 高等流体力学[M]. 西安: 西安交通大学出版社, 1989: 7-10, 305-360.FEI Xiang-lin, HU Qing-kang. Advanced hydrodynamics[M].Xi’an: Xi’an Traffic University Press, 1989: 7-10, 305-360.

[12] 吴建民. 高等空气动力学[M]. 北京: 北京航空航天大学出版社, 1992: 39-54, 164-174.WU Jian-min. Advanced aerodynamics[M]. Beijing: Beihang University Press, 1992: 39-54, 164-174.

[13] 陶文铨. 数值传热学[M]. 2版. 西安: 西安交通大学出版社,1992: 137-182, 416-485.TAO Wen-quan. Numerical heat transfer[M]. 2nd ed. Xi’an:Xi’an Jiaotong University Press, 1992: 137-182, 416-485.

[14] 田红旗. 列车交会空气压力波研究及应用[J]. 铁道科学与工程学报, 2004, 1(1): 83-89.TIAN Hong-qi. Research and applications of air pressure pulse from trains passing each other[J]. Journal of Railway Science and Engineering, 2004, 1(1): 83-89.

[15] 王福军. 计算流体动力学分析[M]. 北京: 清华大学出版社,2004: 1-28.WANG Fu-jun. Computational fluid dynamics analysis[M].Beijing: Tsinghua University Press, 2004: 1-28.

[16] Jeong S, Murayama M, Yamamoto K. Efficient optimum design method using Kriging model[J]. Journal of Aircraft, 2005, 42(2):413-420.