SVPWM调制下逆变器输出电压谐波分析

张雪原

(成都信息工程学院 控制工程系,四川 成都 610225)

在SVPWM调制下,逆变器输出电压不可避免地产生谐波(简称SVPWM谐波),而这些谐波造成交流电机的转矩脉动,增加电机的附加损耗,影响电机效率;因此研究逆变器在SVPWM调制下输出电压的谐波特征并寻找抑制谐波的方法是完全必要的。

文献[1-3]对 SVPWM谐波进行了仿真研究。文献[4]用傅里叶分解的方法分析了SVPWM在过调制方式下的谐波含量变化情况。文献[5]利用傅里叶分解讨论了整流器中 SVPWM谐波含量。

本文基于两电平SVPWM工作原理,得到逆变器输出线电压的解析表达式,并对线电压方程进行傅里叶分解,然后讨论电压谐波随步进频率、输出电压频率和调制电压变化的关系。结果表明,在SVPWM 线性调制下,调制频率和调制电压幅值对谐波含量具有重要的影响。

1 SVPWM逆变器基本原理

三相逆变电路如图 1所示,公共电网的交流电通过整流电路转换为直流电供逆变器使用,在本文中使用直流电源进行等效,直流电经过三相逆变桥逆变成交流,供交流电机使用。

图1 逆变器原理图Fig.1 Schematic diagram of the inverter

在逆变桥中,同一相由上下两个桥臂构成,在正常工作时,上桥臂和下桥臂的通断状态刚好相反,当上桥臂导通时,下桥臂关断,输出正电压;当上桥臂关断时,下桥臂导通,输出负电压。如果把上桥臂导通下桥臂关断的状态记为“1”,把上桥臂关断下桥臂导通的状态记为“0”,则三相逆变桥输出电压向量可以表示为U0(000),U1(100),U2(110),U3(010),U4(011),U5(001),U6(101),U7(111)8个向量,在这8个向量中U0(000)和U7(111)的向量幅值为零,其余6个向量幅值为2UDC/3,依次相差π/3(电角度),这样三相逆变桥开关的不同组合最终输出7个独立的基本电压向量,如图2所示。

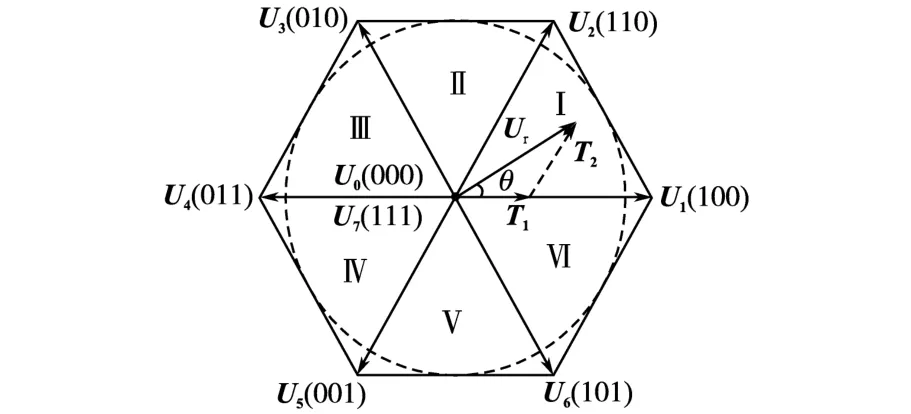
图2 SVPWM调制向量图Fig.2 SVPWM vector diagram

在以6个非零向量为顶点的正六边形内,任意电压向量Ur都可以用相邻的基本电压向量和零向量的组合来等效。等效的方法见图2,如果电压向量Ur作用的持续时间为t,则基本电压向量T1,T2和零向量T0作用的时间t1,t2和t0如下:

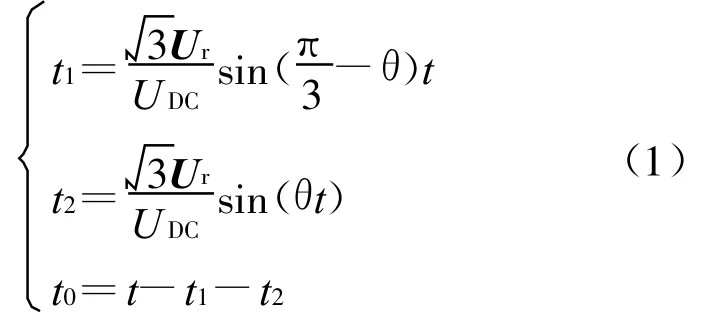
式中:θ为向量Ur与向量T1的夹角;UDC为直流电压。

这种利用伏秒平衡原理通过基本电压向量的组合来等效向量平面上六边形内任意一电压向量的方式称为SVPWM调制方式。

在SVPWM调制下,电压向量的旋转不是匀速的,而是在一个位置呆一段时间,然后跳变到下一个位置,这样走走停停,保证了电场在平均意义下的匀速旋转,把电压向量的这种旋转方式称为步进方式。1 s内的步进次数称为步进频率,每一步停留的时间称为步进时间。

当参考电压按照给定的电压向量轨迹变化时,则称为调制电压。为了使逆变器输出电压为正弦波形,调制电压向量为幅值不变,角度随时间旋转的圆形轨迹。

根据参考电压向量Ur的不同,可以把SVPWM 调制分为3种模式:线性调制模式、过调制模式Ⅰ和过调制模式Ⅱ。当参考电压向量Ur的幅值小于等于六边形内切圆半径时为线性调制模式,参考电压向量Ur由基本向量合成的规则由式(1)确定,非零向量的作用时间与参考电压向量Ur的幅值成正比。当参考电压向量Ur的幅值大于六边形内切圆半径而小于外接圆的半径时为过调制模式Ⅰ,在过调制模式Ⅰ下,参考电压向量Ur的圆形轨迹与六边形的边相交,输出电压向量在六边形内的部分按照圆形轨迹运动,在六边形外的部分沿着六边形的边运动,输出电压向量的实际运动轨迹为圆弧与直线组成。当参考电压向量Ur的幅值等于六边形的外接圆半径时为过调制模式Ⅱ,此时输出电压向量的实际运动轨迹和六边形重合。

2 线电压波形

为了排除负载参数和电压中性点的影响,选择直接对逆变器的输出线电压进行研究。由于线电压输出的对称性,选择A,B相间的电压UAB进行分析即可。由基本向量和逆变桥的开关组合的对应可以得到线电压UAB值与基本电压向量的关系,如表1所示。把向量平面划分为6个扇区,并对扇区依次编号,如图2所示,在第Ⅰ扇区,电压向量U1(100),U2(110)和零向量交替作用,表现在线电压UAB的波形上则为幅值为UDC的脉冲电压和零电压交替出现,在第Ⅱ扇区,电压向量U2(110),U3(010)和零向量交替作用,表现在线电压UAB的波形上则为幅值为-UDC的脉冲电压和零电压交替出现,余下的扇区依此类推。在每个扇区中,只要计算出电压向量的作用时间,也就得到了线电压UAB的PWM波形。

表1 UAB值与基本电压向量的对应关系Tab.1 T he relation between UABand the voltage vector

设逆变器输出电压的周期为T,每个扇区的步数为n,步进时间为T/(6n);对参考电压向量标记为Uml,下标m(m=1,2,3,4,5,6)表示扇区,l(l=0,1,2,3,…,n)表示一个扇区内向量序号(逆时针方向增大),则电压向量Uml与扇区起始位置的夹角为πl/(3n)。电压向量Uml由扇区起始位置和结束位置方向的基本电压向量(Tl1,Tl2)及零电压Tl0合成,3个向量的作用时间分别为tl1,tl2和 tl0,则有

如果把零电压作用时间tl0分为相等的两段插入tl1和 tl2的前面,则可以得到线电压UAB关于时间t的函数(以向量U1(100)位置为时间零点):

对式(3)进行傅里叶分解,即可得到线电压UAB(t)各次谐波的幅值。在SVPWM 调制下,由于线性调制模式是其工作的主要方式,所以本文对这种调制方式下的谐波情况进行分析。

3 步进频率对谐波影响

取调制电压幅值为六边形内接圆的半径(0.577UDC),逆变电压的输出频率为50 Hz,每个扇区的步数为n,则对式(3)进行傅里叶分解,并对1万次以下的谐波进行计算,得到逆变器输出电压总谐波畸变率和步数n的关系,如图3所示。

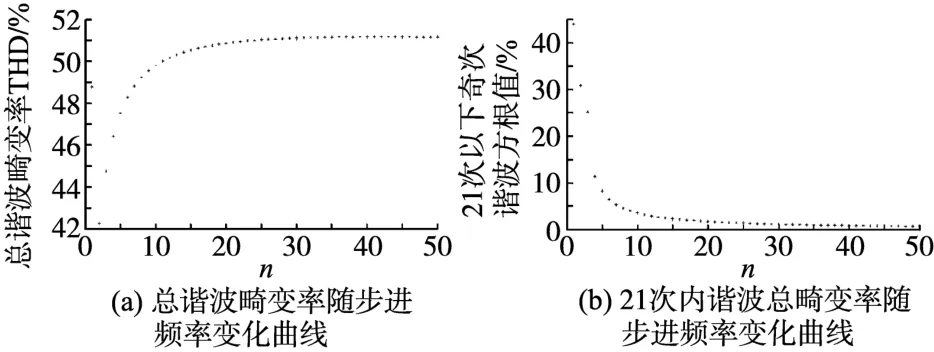
图3 谐波含量与步进频率关系Fig.3 The relation between the harmonics and step frequency

从图3a中可以看出,除了n等于1这点外,逆变器输出电压的总谐波畸变率随n的增加而单调递增;图3b中,21次及以下谐波方根值随n的增加而减小。图3表明,提高开关的工作频率可以使低次谐波的含量大幅度减小,但从整个频带看,总的谐波含量反而略有增加。

图4是步进频率为600,3 000,6 000和9 000时的谐波频率分布。步进频率不同,谐波的频率分布也不同,次数在步进频率及整数倍附近的谐波幅值很大,而其它次谐波幅值较小,步进频率越高,这种现象越明显。

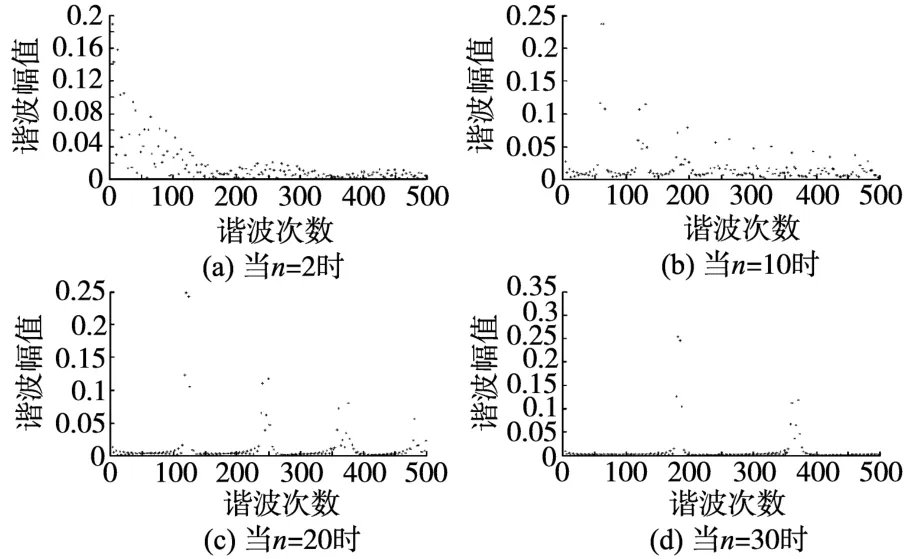
图4 谐波频谱分布Fig.4 Harmonic distribution

这说明,在SVPWM逆变器中,提高开关的工作频率并不能降低谐波的总含量,但开关频率的提高使幅值较大的谐波向高频段发生了转移,从而减小了低次谐波含量,频谱分布发生了变化。低次谐波含量的减小有助于降低交流电机输出转矩的脉动和谐波损耗;但当低次谐波含量减小时,高次谐波含量必然增加,高次谐波含量的增加势必增大交流电机容性电流的幅值,从而使电机绕组匝间电容上流过更大的电流,使电机绕组的绝缘介质发热量增加,局部放电更容易发生,绝缘介质更容易老化失效。

4 输出电压周期对谐波影响

选取SVPWM调制中每个扇区的步数n=2,保持调制电压为内接圆半径不变,改变输出电压的周期,则可以计算出不同周期下的谐波幅值,从而得到各次谐波随输出电压周期的关系,见图5。

图5 谐波幅值随输出电压周期变化曲线Fig.5 T he curves of the harmonics according to the voltage period

计算表明,对于确定的步进频率,输出电压周期(即输出电压的频率)变化对各次谐波的含量没有任何影响。当输出频率变化时,如果每一个扇区的步数不变,即载波比不变,则输出电压中各次谐波含量保持不变;在变频器实际控制中,可能采用分段同步调制的方式,也即载波比在不同的速度区间分段,如果载波比改变,则输出电压的谐波含量相应改变,对应的谐波含量可以根据第3小节的方法进行计算。

5 调制电压对谐波含量的影响

取逆变电压的输出频率为50 Hz,每个扇区的步数为2,改变调制电压的幅值,则可以得到谐波含量随调制电压幅值变化的一组曲线,见图6。

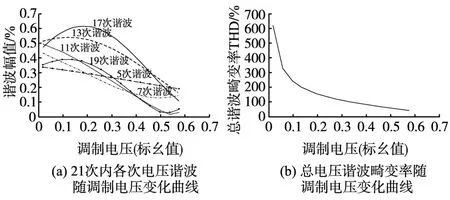
图6 谐波含量随调制电压变化曲线Fig.6 The curves of the harmonics according to the voltage

在图6中,调制电压从0.017UDC到0.577UDC(为最大线性调制电压)间变化。随着调制电压的变化,各次谐波幅值都发生了变化,但总体的趋势是各次谐波幅值随调制电压幅值的增加而减小。随着调制电压的增加,逆变器输出电压的总谐波畸变率快速下降;调制电压对总的谐波畸变率有非常大的影响,当调制电压下降到0.337 UDC时,即下降到最大线性调制电压的58%时,总电压谐波畸变率THD达到了100%,当调制电压下降到最大线性调制电压的10%时,总电压谐波畸变率达到329%,这么高的谐波电压势必对电动机的运行性能产生严重影响。为了减小谐波以便使电动机获得良好的运行性能和减小谐波的损耗,应该使调制电压尽可能大。

6 结论

三相逆变器在SVPWM线性调制下输出电压的谐波主要受步进频率和调制电压的影响。步进频率的变化对总电压畸变率影响不大,但步进频率不同,逆变器输出电压谐波含量的分布发生明显改变。随着步进频率的提高,低次谐波含量减小。调制电压对谐波含量有强烈影响,调制电压越小,逆变器输出谐波含量越大。

在设计逆变器时除了确定合适的步进频率使谐波的分布合理外,还要注意调制电压与直流电压恰当的比值,才能获得良好的电压输出波形。

[1]高莹,谢吉华,陈浩.SVPWM的调制及谐波分析[J].微特电机,2006(7):10-12.

[2]张晟,余海涛,陈小林.SVPWM 型逆变器驱动感应电机电压谐波分析和脉动转矩仿真[J].自动化与仪器仪表,2008(4):83-84.

[3]梅从立,刘国海,廖志凌.空间矢量 PWM谐波分析及其对电机转矩的影响[J].微特电机,2004(7):16-19.

[4]张立伟,刘钧,温旭辉,等.基于基波幅值线性输出控制的SVPWM过调制新算法[J].中国电机工程学报,2005,25(19):13-18.

[5]陈瑶,童亦斌,金新民.基于PWM整流器的SVPWM谐波分析新算法[J].中国电机工程学报,2007,27,(13):76-80.