爆炸焊接界面波的数值模拟＊

李晓杰，莫 非，闫鸿浩，王海涛

（大连理工大学工程力学系工业装备结构分析国家重点实验室，辽宁 大连 116023）

界面波是爆炸焊接过程中常见的现象之一，与焊接质量息息相关。在力学研究领域，爆炸焊接界面波形成机理存在着多种解释，如流体不稳定性机理、刻入机理、漩涡流泻机理和应力波机理等［1］。在运用流体动力学方法分析成波机理的过程中，郑哲敏等［2］指出，爆炸焊接过程中材料强度对界面波的形成起着重要作用。A.A.Akbari Mousavi等［3］借助AUTODYN软件对爆炸焊接斜碰撞过程建立了考虑材料强度的流体动力学有限元分析模型。

本文中，运用光滑粒子流体动力学方法，以Johnson－Cook材料模型和Grüneisen状态方程为基础，建立热塑性流体力学模型，借助ANSYS／LSDYNA 11.0软件对爆炸焊接界面波进行模拟，模拟结果与实验结果［4－5］进行比较。希望对界面波理论研究、爆炸焊接实验及生产预测等有所帮助。

1 计算模型

图1 计算模型Fig.1The calculation model

建立平面二维数值计算模型，使 用 ANSYS／LS－DYNA 11.0软件中的SPH单元进行数值模拟。计算模型如图1所示，上部为运动的复板，复板以给定运动速度和运动方向撞击下部的静止基板，金属板的几何尺寸为20mm×2.5mm 或40mm×2.5mm，使用质点个数为8～25万个。使用钢材为4340钢和A3钢，A3钢的部分Johnson－Cook材料公式参数不详，用纯铁的参数替代。Johnson－Cook材料参数［6］、Grüneisen 状 态 方 程 参数［7］见表1～2。

表1 Johnson－Cook材料模型参数Table 1The parameters of Johnson－Cook model

为了反映爆炸焊接的斜碰撞过程，复板运动形式按炸药滑移爆轰驱动方式设定。复板的碰撞速度vp值可用Taylor公式计算

式中：vd为炸药爆速；β为碰撞角。

由于在滑移爆轰抛掷时，碰撞速度vp的方向是垂直于碰撞角β的角平分线，这样速度vp分量分别为

2 模拟结果

表2 Grüneisen状态方程参数Table 2The parameters of Grüneisen state equation

基于文献［5］中的量纲分析，比波长是3个量纲一量β、¯σ、Re的函数

式中：β为两块金属板碰撞时刻的夹角＝σy／（），为碰撞点强度与动压力之比，倒数P＝1／¯σ，可理解为驻点比压力，简称P为比压。σy为材料静态屈服强度，vf为碰撞来流速度，Re＝ρvfh／η，为雷诺数，h为复板厚度，η为复板金属材料粘性系数，模型碰撞来流速度vf的大小等于爆速vd。

图2 4340钢模拟界面波形貌Fig.2Simulated 4340steel interface waves

由于Johnson－Cook材料模型中的物质本构方程不涉及粘性流体模型中的粘性系数η，也就是说模拟结果与实验研究中有关于雷诺数Re的结论没有同向可比性，所以主要针对比压P相关实验结论进行比较。

图3 比波长－比压关系曲线Fig.3The¯λ－Pcurves

首先，选用4340钢材料，几何尺寸为20mm×2.5mm，保持碰撞角β＝13°，通过改变爆速vd改变比压P，比压P的变化范围为16～150，模拟的界面波如图2。其中4种界面波为爆炸焊接生产实际中可能出现的波形形貌，即从平直界面向带有前后涡旋界面过渡的4个阶段。

选用读取波长平均值的方法，借助后处理软件LSPREPOST可以实现波长测量。比波长－比压关系曲线如图3所示，其中实验公式为

类似地，选用A3钢材料，几何尺寸为40mm×2.5mm，保持碰撞角β＝26°，比压P的变化范围为16～150，比波长－比压关系曲线如图3所示。对应的界面波形貌见图4。

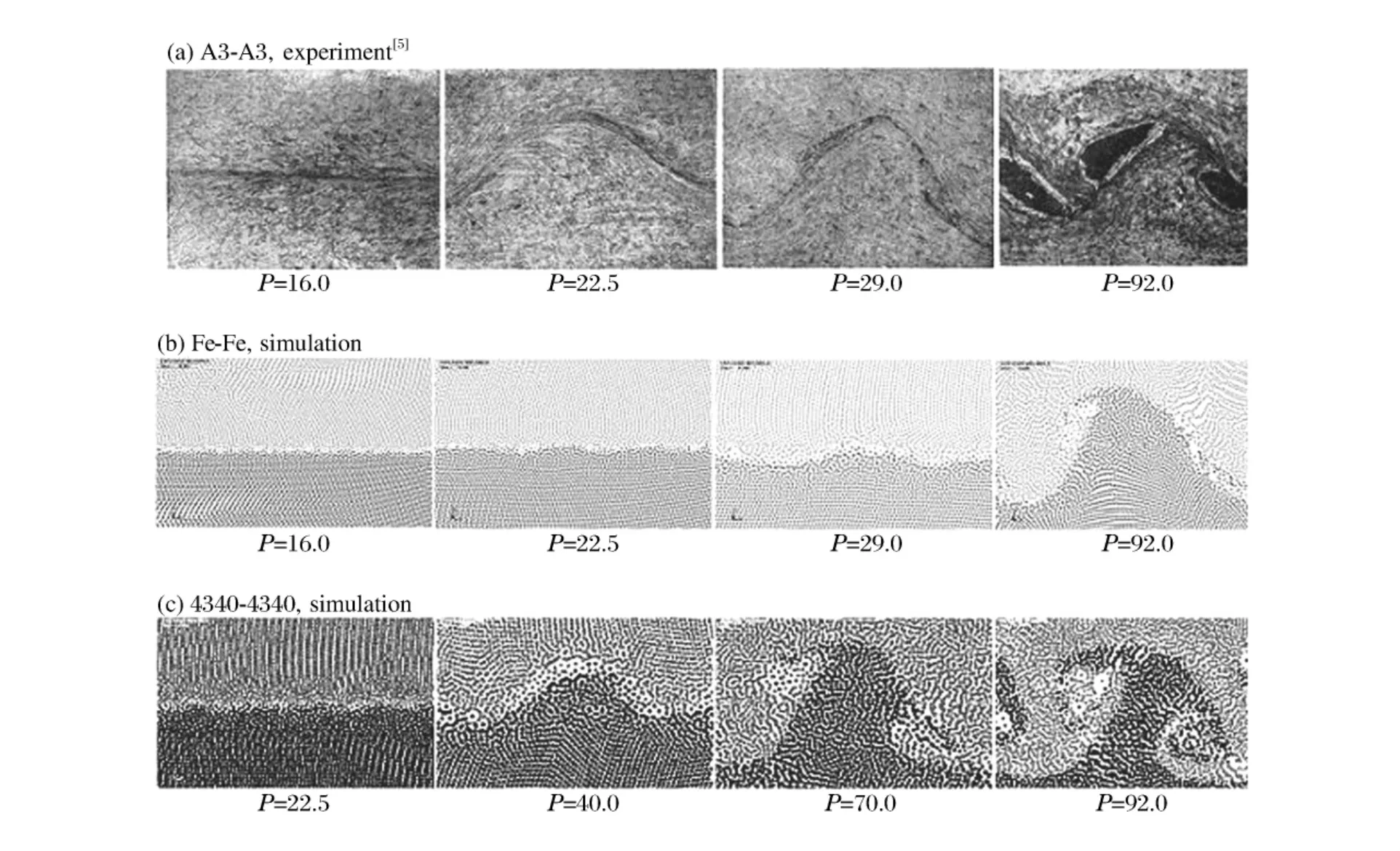
图4 实验和模拟的界面波形貌Fig.4Interface waves of experiment and simulation

3 模拟与实验的比较分析

4340钢的模拟与实验的比较表明，模拟结果与张登霞等［4－5］的实验公式符合得较好。从总体上看，模拟的比波长比实验公式计算的稍大，但两条曲线符合较好。比压P在22.5～50区段，误差最大点在P＝40，为56.14%；在50～100区段，误差最大处在P＝70，为22.12%；100以上区段，误差最大处在P＝140，为4.67%。

A3钢的模拟与实验的比较表明，模拟结果与实验符合较好。从总体上，模拟结果大于实验的。比压P在22.5～50区段，误差最大点在P＝40，为16.80%；在50～100区段，误差最大处在P≈92，为15.43%；在100以上区段，误差最大处在P≈120，为11.13%。从波形图上可以看出，随比压P的增大，波形从平直界面向带有前后涡旋的波界面发生着逐步地演化，对比可知，模拟界面波的演化要滞后于实验。

误差主要来源于3个方面：（1）测读误差。4340钢模拟过程中粒子的尺寸与板厚的比为1∶125，因此在读取波长值时，错读一个粒子的距离便会造成0.8%的测读误差。同样地，A3钢模拟中单个粒子测读误差为2%，取平均波长的测读方法可以减小测读误差，但是界面波不清晰时测读误差会较大。（2）材料模型以及实验公式参数误差。本文中使用的是Johnson－Cook材料模型，模拟中A3钢不详参数用纯铁参数替代，势必会造成误差，而真实Johnson－Cook材料参数需要相关实验确定。另外，与4340钢模拟进行对比的实验公式来源于A3钢材料的爆炸焊接实验，同样也会产生误差，应当对经验公式作出适当的修正。（3）能量耗散项可能带来误差。两板发生高速碰撞，板中会有冲击波产生，模拟过程中用＊CONTROL＿BULK＿VISCOSITY的默认值提供冲击问题所必须的能量耗散，模拟界面波比实际发展滞后的原因可能部分来源于耗散项的设置不当。

文献［5］中证明了爆炸焊接界面波形成机理属于流体弹塑性范畴，来源于对低碰撞速度段和高碰撞速度段比波长－比压实验曲线走势的分析，低碰撞速度段对应比压P在22.5～50，高碰撞速度段对应50～100。从模拟结果可见，本文中使用的热塑性流体力学模型同样可以印证该结论在22.5～100上的适用性。除此之外，对比压P＞100区段，即更高碰撞速度段，模拟曲线与实验也符合得较好。另外，通过各区段最大误差的比较可知，本文中模型更适用于高碰撞速度段爆炸焊接界面波的模拟。

4 结 论

运用SPH方法对爆炸焊接界面波进行模拟，优点之一就是它能够很好地再现爆炸焊接过程中的界面波形貌，这为爆炸焊接界面波的理论研究提供了一个新的有利工具。模拟过程中存在的不足主要体现在材料参数的选择上，A3钢的Johnson－Cook材料模型参数由纯铁的替代，势必影响模拟的效果。另外，本文中使用的热塑性流体力学模型是以Johnson－Cook材料模型和Grüneisen状态方程为基础建立起来的，尝试运用其他的材料模型和状态方程对爆炸焊接界面波进行模拟研究也是有必要的。总之，从数值模拟的角度研究界面波附近区域物理场的分布与变化是必要的。

［1］邵丙璜，张凯.爆炸焊接原理及其工程应用［M］.大连：大连工学院出版社，1987：346－347.

［2］郑哲敏，谈庆明.爆炸复合界面波的形成机理［J］.力学学报，1989，21（2）：129－139.

ZHENG Zhe－min，TAN Qing－ming.Mechanism of wave formation at the interface in explosive welding［J］.Acta Mechanica Sinica，1989，21（2）：129－139.

［3］Akbari Mousavi A A，Al－Hassani S T S.Numerical and experimental studies of the mechanism of the wavy interface formations in explosive／impact welding［J］.Journal of the Mechanics and Physics of Solids，2005，53（11）：2501－2528.

［4］张登霞，李国豪.低炭钢爆炸焊接界面波与板材无量纲强度关系的试验研究［J］.爆炸与冲击，1983，3（2）：23－29.

ZHANG Deng－xia，LI Guo－hao.An experimental relation between interface wave form of explosion welding mild steel and material dimensionless strength［J］.Exlosion and Shock Waves，1983，3（2）：23－29.

［5］张登霞，李国豪，周之洪，等.材料强度在爆炸焊接界面波形成过程中的作用［J］.力学学报，1984，16（1）：73－80.

ZHANG Deng－xia，LI Guo－hao，ZHOU Zhi－hong，et al.Effect of material strength on forming process of explosive welding interface wave［J］.Acta Mechanica Sinica，1984，16（1）：73－80.

［6］Johnson G R.Fracture characteristic of three metals subjected to various strains，strain rates，temperatures and pressures［J］.Engineering Fracture Mechanics，1985，21（1）：31－48.

［7］王礼立.应力波基础［M］.2版.北京：国防工业出版社，2005：205－206.