本构模型对复合材料中X射线热击波数值模拟结果的影响＊

黄 霞，汤文辉，蒋邦海

（国防科技大学理学院技术物理研究所，湖南 长沙 410073）

近年来，复合材料以低密度、高模量、良好的隔热和防热性能广泛应用于航空、航天等领域，成为国防工业部门的一种重要工业材料。例如导弹的头锥和蒙皮，航天飞机的鼻锥、机翼和尾翼等关键部件均采用碳纤维增强复合材料。在航空、航天等领域中，航天器的外部环境非常复杂，可能面临高速碰撞、X射线辐照等动载荷环境。在脉冲X射线辐照下，大量射线能量迅速沉积在材料表层，由外向内迅速下降，材料内有很大的温度、压力梯度。另外，受照材料由于比内能的快速增大而发生绝热膨胀，当辐照量足够大时，迎光面的物质会发生汽化，汽化了的物质向外喷射，并对材料产生反冲作用。这些因素的共同作用将在材料内部形成非定常的应力波，即X射线热击波［1］。随着复合材料在导弹或航天器中的大量应用，了解X射线脉冲辐照引起的热击波在复合材料中的传播规律，并正确地评估它对热激波的防护能力就显得越发重要。但长期以来很多这方面的研究工作都是针对金属材料的，或将各向异性材料近似利用各向同性理想弹塑性本构模型进行数值模拟计算。20世纪90年代以来，有关研究结果表明，利用各向同性本构模型进行数值模拟得到的金属中X射线热击波应力峰值衰减曲线与实验符合较好，而在复合材料中则是实验得到的峰值衰减比数值模拟快，实验获得的应力峰值比数值模拟低，这是数值模拟时把复合材料用各向同性本构模型近似所带来的偏差［2］。

实验表明各向异性和应变率相关性是大多数复合材料的力学特性，那么他们不可避免地将对X射线热击波的传播规律带来影响，因此数值模拟中使用的本构模型应该计及这些特征。本文中，以碳酚醛中的一维X射线热击波数值模拟为例，定量分析修正的各向异性PUFF物态方程、率相关的Tsai－Hill屈服准则对热击波传播规律的影响，试图证明利用各向异性动态本构模型获得的结果，比各向同性理想弹塑性、各向异性理想弹塑性本构模型，与实验结果更接近。

1 本构模型

1.1 修正的各向异性PUFF物态方程

在一维应变的假设条件下，εy＝εz＝εxy＝εxz＝εyz＝0，σxy＝σxz＝σyz＝0，各向异性材料弹性阶段应力与应变之间的关系可用广义 Hooke定律表示为σx＝cxxεx，σy＝cxyεx，σz＝cxzεx，其中cij为与弹性模量、泊松比和剪切模量相关的刚度矩阵系数。

在大多数流体动力学程序中，将容变律和畸变律解耦处理，反映在算法上就是将应力分解为平均应力和偏应力，即σij＝pδij＋sij，并分别利用物态方程和本构关系来计算。若定义压为正，弹性阶段平均应力可表示为

由于式（1）的线性关系只在压力很低的情况下才成立，通常引入物态方程来计算平均应力，以考虑材料体积变化的非线性特征。对于X射线辐照问题，材料状态比较复杂，要求所使用的物态方程既要能描述温度相对较低的冲击压缩状态，又要能处理X射线能量沉积和流体动力学相互耦合所形成的状态。即在受光面附近，在能量沉积比流体动力学过程快得多时，材料处于高温高压，但密度接近于初始值的状态，以及当流体动力学稀疏发展后，体积膨胀的高温低密度状态［3－4］。通常采用PUFF物态方程来描述，在压缩区

在膨胀区

式中：p是压力，v是比体积，ρ＝1／v为密度，e是物质的比内能，Γ0是Grüneisen系数，γ为比热比，es为升华能，N＝／（Γ0es）。式（2）为Grüneisen物态方程，与式（3）在v＝v0处连续，式（3）能很好地从固态区过渡到气态区［5］。

将式（2）～（3）展开成关于μ的多项式级数形式，在压缩区

在膨胀区

式中：μ＝（v0－v）／v，表示体积的相对变化，近似等于体应变θ＝εx；c0、s为冲击波速关系式中根据实验拟合的材料常数。

式（4）～（5）是适用于各向同性材料的物态方程的级数形式，没有反映材料的各向异性特点。结合式（1）可得到弹性阶段体现材料各向异性特征的修正物态方程［6－7］，在压缩区

在膨胀区

式中：＝＝（cxx＋cxy＋cxz）／3，反映材料的各向异性，称为等效体积模量。在各向同性的极限条件下，和退化为体积模量K＝，物态方程退化为经典的PUFF物态方程。

在塑性变形阶段，变形依赖于历史，应力应变关系用增量形式表示，则平均应力增量可表示为

同样，将式（8）引入到式（4）～（5）中，可得到塑性阶段体现材料各向异性特征的修正物态方程的增量形式，在压缩区

在膨胀区

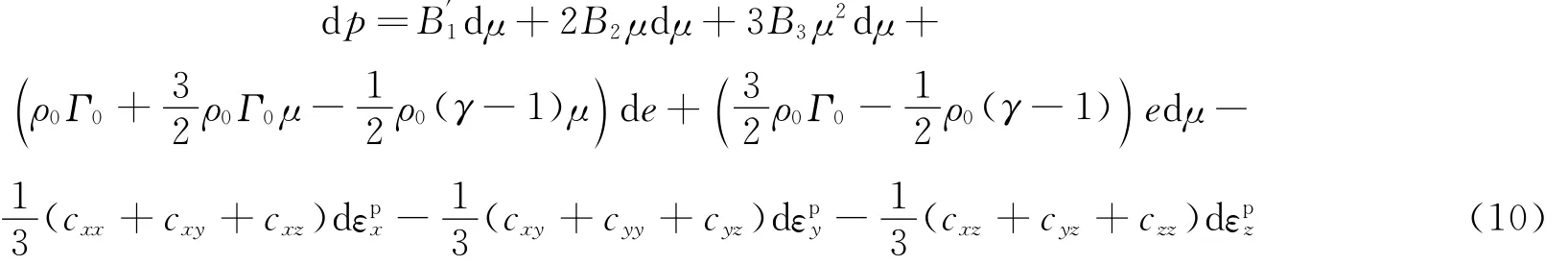
至此，给出了适用于各向异性材料的修正PUFF物态方程，据此物态方程计算得到的平均应力既考虑了体积变化的非线性特征，又体现了材料的各向异性性能。

1.2 率相关的Tsai－Hill屈服准则

屈服准则是判断材料处于弹性阶段还是塑性阶段的准则，是材料本构模型的重要组成部分，在数值模拟中，屈服准则的选取对材料塑性阶段的应力计算具有很大影响。对于各向异性材料，常用的屈服准则有Tsai－Hill准则和Tsai－Wu准则，由于Tsai－Hill准则在参数确定上比较简单，因而应用得更为广泛。在一维应变条件下Tsai－Hill准则基本形式为

由于大多数各向异性材料都具有明显的应变率相关性特点，引入率相关的Tsai－Hill屈服准则［8－9］，屈服强度依赖于应变率

式中：R（˙ε）为应变率因子，β为实验获得的参数为参考应变率，并且认为应变率˙ε为等效塑性应变率。则率相关的Tsai－Hill屈服准则可写为－1＝0，得到率分离形式的屈服准则为

2 算例及分析

以碳酚醛靶中的一维应变热击波为例，讨论本构模型对热击波数值模拟结果的影响。碳酚醛（简称TF）是一种正交各向异性复合材料，3个材料主轴方向分别为纤维布经向、纬向和纤维铺层厚度方向。假设初始时纤维布经向沿x方向，纬向沿y方向，铺层厚度沿z方向，材料x方向的尺寸为1cm，其他2个方向的尺寸为无限大，X射线平行于x方向入射。能谱为1keV的黑体谱，能通量为200J／cm2、时间谱为0.1μs的矩形谱。数值模拟采用3种本构模型，即各向同性理想弹塑性本构模型1、各向异性理想弹塑性本构模型2和各向异性动态弹塑性本构模型3。模型1采用传统的PUFF物态方程与Mises屈服准则，模型2采用修正的各向异性PUFF物态方程与率无关的Tsai－Hill屈服准则，模型3采用修正的各向异性PUFF物态方程和率相关的Tsai－Hill屈服准则。3种模型均采用相同的物态方程参数，TF材料物态方程参数分别为：ρ0＝1.38g／cm3，c0＝2.35km／s，s＝1.66，Γ0＝2.32，γ＝1.4，es＝5.15kJ／g，本构参数如表1所示。数值模拟所用程序采用显式有限元方法编写，网格单元的空间步长为10μm，时间步长为0.1ns。

表1 TF材料本构参数Table 1Constitutive parameters of TF material

图1 不同本构模型的σx应力剖面图Fig.1The profiles ofσxby different constitutive models

图2 应力峰值随靶厚的衰减曲线Fig.2Attenuation curves of peak stress versus thickness of target

图3 应力峰值的相对差值随靶厚的变化曲线Fig.3Relative error curves of peak stress versus thickness of target

在材料的X射线辐照问题中，热击波应力峰值及其衰减趋势是衡量材料抗辐照能力好坏的重要指标。材料x方向主应力σx的剖面图，如图1所示；材料中x方向热击波峰值随辐照深度的衰减曲线，如图2所示；应力峰值的相对差值随靶厚的变化曲线，如图3所示，其中σi，m表示根据第i种模型模拟得到的应力峰值；坐标分别为3.75和6.25mm的2个单元的σx应力历史曲线，如图4所示。

从图1中可以看出，在辐照结束前，能量沉积的速度远快于流体动力学过程，材料处于高温高压但密度接近于初始值的状态，还来不及发生变形，应力主要由能量沉积控制，根据不同模型计算得到的σx峰值比较接近；辐照结束后，随着热击波在靶中的传播，应力值迅速衰减，各向异性强度效应显现，由于模型2中的等效体积模量比模型1中的各向同性体积模量小，使得σx峰值较小；考虑了应变率强化效应后，σx峰值在率相关屈服准则的作用下进一步减小。

从图2～3中可以进一步直观地看出，相比各向同性理想弹塑性本构模型，根据各向异性动态模型模拟得到的热击波峰值较小，衰减速度更快，且这种差距随热击波的传播深度总体上呈逐渐增大的趋势。根据图4可知，3.75mm处模型3的应力峰值比模型1的峰值小24.5%，而6.25mm处相应的峰值则小34.1%。

图4 不同模型定点位置的σx应力历史曲线Fig.4The history curves ofσxat fixed positions by different constitutive models

通过以上对数值模拟结果的细致比较分析可知，TF材料的各向异性和应变率相关性对X射线热击波的传播规律带来的影响比较显著。20世纪90年代以来，有关研究结果发现，对于复合材料利用各向同性本构模型模拟得到的应力峰值比实验值高，峰值衰减比实验慢，而我们采用各向异性动态本构模型计算得到的X射线热击波应力峰值的衰减规律在定性上和实验结果比较一致。

此外，我们还改变数值模拟条件，分别对X射线谱为3keV的黑体谱，能通量为100、400J／cm2，沿TF材料厚度方向、纤维纬向辐照时材料中的X射线热击波进行了数值模拟，均得到了上述结论，表明该结论具有普适性。

3 结 论

以TF材料中的一维X射线热击波数值模拟为例，对材料的各向异性、率相关性给X射线热击波传播规律带来的影响进行了定量分析。数值模拟结果表明：与各向同性、各向异性理想弹塑性本构模型相比，利用率相关的各向异性动态弹塑性本构模型获得的热击波峰值较小、峰值衰减较快，与相关实验结果更接近。

［1］汤文辉，张若棋，赵国民.脉冲 X射线诱导的热击波［J］.高压物理学报，1995，9（2）：107－110.

TANG Wen－hui，ZHANG Ruo－qi，ZHAO Guo－min.Thermal shock wave induced by impulsive X－ray［J］.Chinese Journal of High Pressure Physics，1995，9（2）：107－110.

［2］蒋邦海.正交织物复合材料的动态本构模型及热激波研究［D］.长沙：国防科技大学，2006.

［3］张若棋，汤文辉，赵国民.影响 X光热激波数值模拟结果的若干因素［J］.高压物理学报，1998，12（3）：161－167.

ZHANG Ruo－qi，TANG Wen－hui，ZHAO Guo－min.Several influential factors on numerical simulated results for the X－ray thermal shock wave［J］.Chinese Journal of High Pressure Physics，1998，12（3）：161－167.

［4］张若棋，汤文辉，赵国民.X射线热击波的数值计算［J］.抗核加固，1993，10（1）：15－23.

［5］周南，乔登江.脉冲束与辐照动力学［M］.北京：国防工业出版社，2002：207－210.

［6］Anderson C E，Cox P A，Johnson G R，et al.A constitutive formulation for anisotropic materials suitable for wave propagation computer programsⅡ［J］.Computational Mechanics，1994，15：201－223.

［7］Lukyanov A A.An equation of state for anisotropic solids under shock loading［J］.The European Physical Journal B，2008，64：159－164.

［8］蒋邦海，张若棋.一种碳纤维织物增强复合材料应变率相关的各向异性强度准则［J］.爆炸与冲击，2006，6（4）：333－338.

JIANG Bang－hai，ZHANG Ruo－qi.Strain rate－dependent Tsai－Hill strength criteria for a carbon fiber woven reinforced composite［J］.Explosion and Shock Waves，2006，26（4）：333－338.

［9］李永池，谭福利，姚磊，等.含损伤材料的热粘塑性本构关系及其应用［J］.爆炸与冲击，2004，24（4）：289－298.

LI Yong－chi，TAN Fu－li，YAO Lei，et al.Thermo－viscoplastic constitutive relation of damaged materials with application［J］.Explosion and Shock Waves，2004，24（4）：289－298.