脆性材料动态强度应变率效应*
严 成,欧卓成,段卓平,黄风雷
(北京理工大学爆炸科学与技术国家重点实验室,北京 100081)
脆性材料在动态加载下比在准静态加载下具有更高的承载能力,或者说,材料的动态破坏强度高于静态破坏强度。这种现象常被称为材料动态破坏强度的应变率效应。该问题的研究深受关注。
一方面,作为材料静态强度理论的自然拓展,人们假设材料动态强度是与应变率相关的材料特征参数,并结合各种各样的瞬时破坏理论如最大应力准则、最大应变准则和最大应变能准则等,试图建立各类材料的动态强度与应变率之间的函数关系,并且提出了许多经验或半经验的应变率相关的动态破坏准则[1-6]。然而实验数据离散度大,妨碍了人们对于规律的总结,难以满足科学研究甚至工程应用的需要[7]。此外,在探索材料动态破坏的应变率效应的物理机理方面也遇到很大困难。
另一方面,从物理机制角度看,材料动态破坏是材料内部原子键、分子键破裂,微缺陷生成及发展乃至宏微观孔洞聚合,裂纹扩展等因素导致的一个复杂的损伤演化过程;而完成这一过程必然需要一定的时间,另外时间也是表示应变率的重要因素。基于此,学者们开始关注并提出了众多与时间相关的动态破坏准则。如 B.Steverding 等[8]提出了临界时间准则,V.S.Nikiphorovski等[9]提出了冲量准则,用来表征材料动态破坏的时间特征;J.F.Kalthoff等[10]、D.A.Shockey 等[11]、K.Ravi-Chandar等[12]等相继提出了材料特征时间的概念,认为材料动态破坏存在一个与材料性质相关的特征时间参数;N.Morozov等[13]证明了矩形脉冲作用下动态应力强度因子KI(t)的发散性质,说明瞬时动态断裂准则存在严重缺陷,并提出了有限结构-时间破坏准则,认为材料的动态破坏将由破坏生成时间τ和临界破坏尺寸d这2个材料参数决定。有限结构-时间破坏准则反映材料动态破坏过程的时间和空间两方面的特征。尤其是临界破坏尺寸的引入,更是当前临界距离理论[14]和有限断裂力学[15]理论的核心。此外,戚承志等[16]指出:时间因素的引入加深了人们对于材料变形及破坏现象的认识,使时间因素显现出来,成为决定性因素之一;钱七虎等[17]认为:材料的变形与破坏有时间特性,即材料变形及破坏依赖于时间因素。
最近,D.M.Cotsovos等[7]提出动载荷下材料的动态响应行为主要是由材料的惯性和加载波特性所决定的,并使用有限元分析结合材料静态参数得到了与材料动态响应实验数据符合较好的数值结果。
与静态破坏相比,动态破坏因与时间相关,使强度性质表现出本质上不同的特点。一方面需要考虑破坏的时间过程;另一方面,由于考虑时间因素,破坏过程是瞬态非平衡过程,惯性效应及状态的非均匀性成为需要考虑的因素。基于上述考虑,本文中在一维应力条件下,结合有限结构-时间破坏准则[13],对动态拉伸载荷下脆性材料动态破坏强度的应变率效应进行理论分析,拟得到材料动态破坏强度与应变率之间关系的解析表达式,并对结果进行必要的分析和讨论。
1 理论模型及求解
如图1所示,考虑半无限长均匀线弹性杆在动态拉伸载荷下的破坏问题。设杆的左端与坐标原点重合。从t=0时刻开始,杆端受到动载荷(ξ)=σ(0,t)的作用。于是,将产生一维应力弹性平面波在杆中由左向右传播。假设x=xc为该杆的最薄弱截面,称之为特征破坏截面,当外载荷满足一定的破坏条件时,杆将在特征破坏截面处发生破坏。
按照上述模型,其运动方程为

式中:u=u(x,t)为待求解的位移场;ρ是一维应力弹性波速;E为弹性模量,ρ为杆材料密度。杆左端边界条件为

图1 杆中一维应力波Fig.1 One-dimensional stress wave in a bar

假设初始时刻杆处于静止状态,则有初始条件
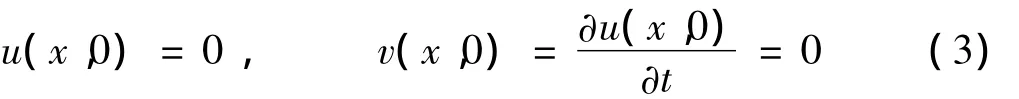
式(1)~(3)构成本模型的定解问题。
方程(1)是标准的一维波动方程。在初始条件(2)和边界条件(3)下,易得到该定解问题的通解[18]

图2 边界条件Fig.2 Boundary condition

以下,将写出给定边界条件下通解(4)的表达式。假设边界动态拉伸载荷为一梯形脉冲(见图2)
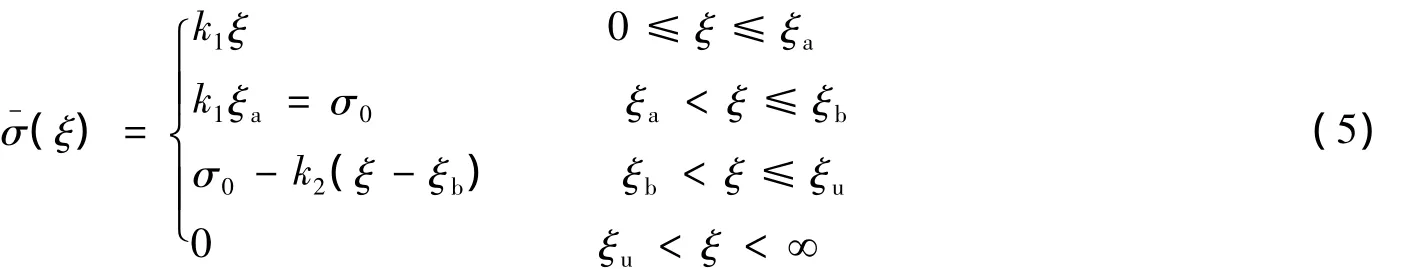
式中:k1、k2为加载曲线的斜率,而ξa、ξb、ξu为边界加载曲线上各段直线分界所对应的时间点。
将边界条件(5)代入通解(4),可得杆中位移场u(x,t)、应变场ε(x,t)和应力场σ(x,t)如下

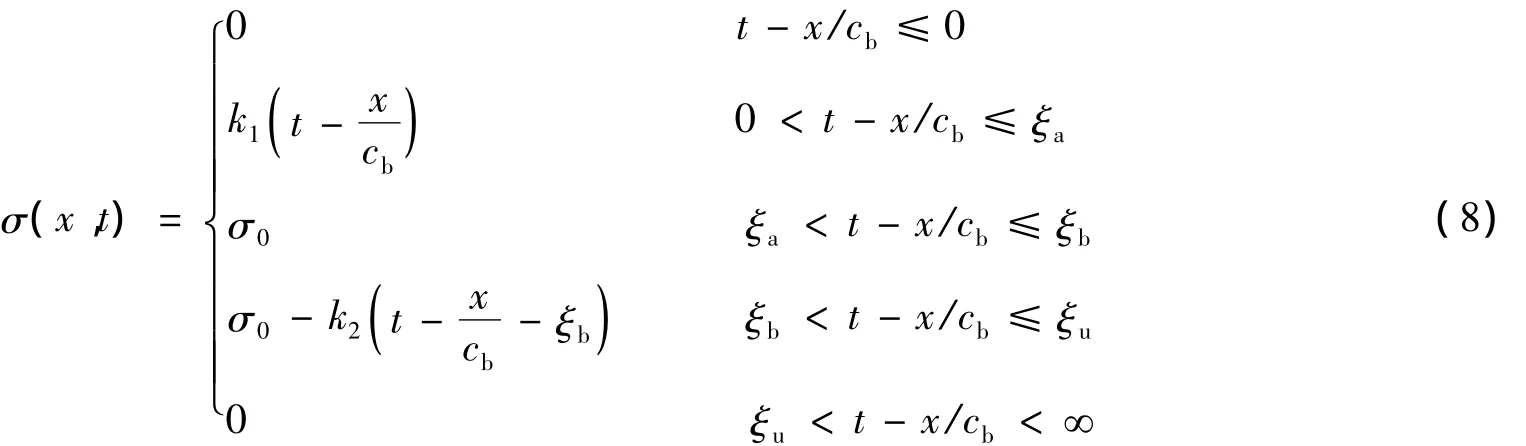
按照 N.Morozov 等[13]的理论,结构-时间准则可写成

式中:τ是破坏生成时间,δ是材料破坏特征长度,σs为材料静态拉伸强度。
如前所述,设材料在t=tc时刻于特征破坏面x=xc处发生破坏。xc/cb为波传播到破坏点的时间;由于应力波在线弹性材料中传播时波形不变,因此,ta、tb、tu分别对应于边界载荷波形中的ξa、ξb、ξu;记Δ为从ta至完全破坏的时间。注意,当将式(8)代入破坏准则式(9)时,对于不同形式的边界载荷(即载荷幅度、加载率以及载荷作用时间与材料破坏生成时间的关系),材料动态破坏准则的具体数学表达形式是不同的。按照图1所示的边界载荷形式,断裂准则呈如下3种形式。

图3 经过x c的入射波形Fig.3 Temporal curves at x=x c
(1)若xc/cb≤tc-τ<tc≤ta,如图3(a)所示,有
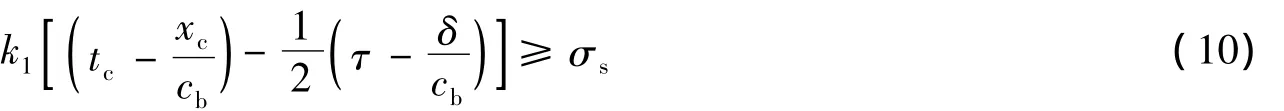

(2)若ta<tc-τ<tc≤tb,如图3(b)所示,有

(3)若xc/cb<tc-τ≤ta≤tc≤tb,如图3(c)所示,则有
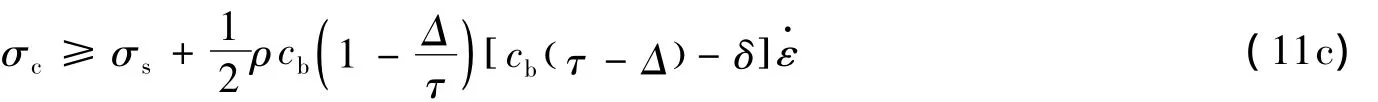
式中:σc是使材料发生破坏的边界应力幅值,也就是所谓的动态破坏强度;0≤Δ≤τ。
2 结果分析
由式(11)可以看出,对于不同的边界载荷形式,材料表现出不同的动态破坏强度。换言之,动态破坏强度不仅与加载率和材料静态性质(破坏强度、动态破坏生成时间和动态破坏特征长度)相关,还依赖于外载荷波形与材料特征参数的关系。这意味着,与静态破坏强度是材料的内禀性质完全不同,材料的动态破坏强度不是材料的内禀特征性质。也就是说,同一种材料在不同的外载荷条件下会表现出不同的动态破坏强度,动态破坏强度的应变率效应表现出明显的结构响应特征。事实上,动态破坏强度不是材料的内禀性质这一概念已开始得到一些学者的关注。最近,D.M.Cotsovos等[7]对脆性材料动态破坏过程进行了有限元数值分析,指出导致动态材料强度的主要因素是材料的结构动态响应和入射脉冲结构特征以及他们之间的关系,而不断提高的材料强度并不能视作是材料的内禀性质;并且,由于所谓的动态破坏强度已不再具有材料内禀特征参数的特征,而以“动态临界承载能力”来形容更加贴切,从而可以减少不必要的概念混淆。显然,上述思想与本文的理论结果是吻合的。
由式(11)还可看出,材料的动态临界承载能力可由外载荷和材料静态参数以及破坏生成时间和特征长度完全确定,这是材料动态破坏应变率效应的结构响应特征导致的必然结果。实际上,D.M.Cotsovos等[7]也曾在有限元数值模拟中得到类似的结果,指出:脆性材料的动态临界承载能力可由外载荷形式、材料静态破坏强度以及其他材料静态特征参数如质量密度和弹性常数等完全确定。按照这一结果,在脆性材料动态破坏研究中已无须再寻找动态破坏参数,这无论对材料动态破坏的理论研究还是实际工程应用都具有重大意义。

另一方面,若σ0<σc,则材料在入射脉冲的整个上升前沿都无法满足破坏准则,使得材料破坏只可能产生于入射脉冲的平台区,由此可确定材料动态破坏的下限。令σ0=σs且τ<T,此时破坏准则为式(11b),故有σc,min=σs,即材料动态临界承载能力的下限为其静态破坏强度。此外,类似地容易推知,当入射脉冲幅值满足σs<σ0<σc时,有σs=σc,min<σc<σc,max。上式表明,随着边界载荷的不同特征,材料动态临界承载能力可以取到静态强度与最大动态临界承载能力之间的一切值,这正是导致动态临界承载能力实验结果离散度较大的内在因素。
3结论
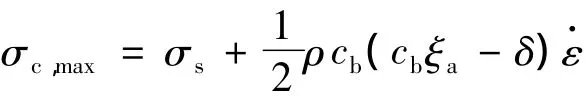
[1]Grady D E.The spall strength of condensed matter[J].Journal of the Mechanics and Physics of Solids,1988,36(3):353-384.
[2]Dekel E,Eliezer S,Henis Z,et al.Spallation model for the high strain rates range[J].Journal of Applied Physics,1998,84(9):4851-4858.
[3]Murray N H,Bourne N K,Rosenberg Z,et al.The spall strength of alumina ceramics[J].Journal of Applied Physics,1998,84(2):734-738.
[4]Diaz-Rubio FG,Perez JR,Galvez V S.The spalling of long bars as a reliablemethod ofmeasuring the dynamic tensile strength of ceramics[J].International Journal of Impact Engineering,2002,27(2):161-177.
[5]Brara A,Klepaczko JR.Experimental characterization of concrete in dynamic tension[J].Mechanics ofMaterials,2006,38(3):253-267.
[6]Weerheijm J,van Doormaal JCA M.Tensile failure of concrete athigh loading rates:New test data on strength and frac-ture energy from instrumented spalling tests[J].International Journal of Impact Engineering,2007,34(3):609-626.
[7]Cotsovos D M,Pavlovic M N.Numerical investigation of concrete subjected to high rates of uniaxial tensile loading[J].International Journal of Impact Engineering,2008,35(5):319-335.
[8]Steverding B,Lehnigk SH.Response of cracks to impact[J].Journal of Applied Physics,1970,41(5):2096-2099.
[9]NikiforovskiiV S,Shemyakin E I.Dynamic fracture of solids[M].Novosibirsc:Novosibirsk University Press,1979:271.
[10]Kalthoff JF,Shockey D A.Instability of cracks under impulse loads[J].Journal of Applied Physics,1977,48(3):986-993.
[11]Shockey D A,Erlich D C,Kalthoff J F,et al.Short-pulse fracture mechanics[J].Engineering Fracture Mechanics,1986,23(1):311-319.
[12]Ravi-Chandar K,KnaussW G.An experimental investigation into dynamic fracture:Ⅰ.Crack initiation and arrest[J].International Journal of Fracture,1984,25(4):247-262.
[13]Morozov N,Petrov Y.Dynamic of fracture[M].Heidelberg,Berlin:Springer,2000:3-5;28-30.
[14]Taylor D.The theory of critical distances[J].Engineering Fracture Mechanics,2008,75(7):1696-1705.
[15]Taylor D,Cornetti P,Pugno N.The fracturemechanics of finite crack extension[J].Engineering Fracture Mechanics,2005,72(7):1021-1038.
[16]戚承志,赵跃堂,郭志昆,等.材料时间性破坏准则及其内在联系[J].世界地震工程,2002,18(2):56-60.
QICheng-zhi,ZHAO Yue-tang,GUO Zhi-kun,et al.The temporal fracture criteria ofmaterial and their intrinsic relationship[J].World Earthquake Engineering,2002,18(2):56-60.
[17]钱七虎,戚承志.岩石、岩体的动力强度与动力破坏准则[J].同济大学学报:自然科学版,2008,36(12):1599-1605.
QIAN Qi-hu,QICheng-zhi.Dynamic strength and dynamic fracture criteria of rock and rockmass[J].Journal of Tongji University:Natural Science,2008,36(12):1599-1605.
[18]Achenbach J D.Wave propagation in elastic solids[M].Amsterdam,London:North-Holland Publishing Company,1973:21-23;29-30.

