地震类型对加筋土挡土墙长期蠕变后动力响应的影响

王向余,刘华北,宋二祥

(1.清华大学土木工程系结构工程与振动教育部重点实验室,北京 100084;2.美国纽约城市大学土木工程系,纽约 10031)

加筋土挡土墙涉及面板、筋材、填土和地基等多种材料,在地震作用下,其动力反应特性十分复杂[1-2],至今,人们对其抗震机理的理解尚不够深入,这也使得目前的抗震设计方法还存在许多缺陷.另外,对于工程上应用越来越多的黏性土填料,由于它和土工合成加筋材料都具有明显的蠕变效应,墙体运行多年后的受力和变形状态会发生较大变化[3-5],这种变化可能会影响之后地震作用下墙体的工作性能.然而,鉴于在本构模型上同时描述土体蠕变效应和动力特性具有一定困难,目前考虑土体蠕变效应的加筋土挡土墙长期蠕变后地震动力响应特性的数值研究还很缺乏[6],人们对此的认识也非常模糊.为此,本文以一8m高黏性土填土的混凝土块面板式土工格栅加筋挡土墙为例,同时考虑土体与筋材蠕变效应,对其经历5a静力蠕变后再遭遇地震作用的整个过程进行了有限元模拟分析,并重点研究了不同类型地震波的影响,在此基础上对加筋土挡土墙的工程设计提出了一些合理化建议.

图1 加筋土挡土墙计算模型Fig.1 Computational model of reinforced soil retaining wall

1 有限元模型

计算模型如图1所示.土体(填土和地基土)采用实用弹塑-黏塑性模型[7-8]模拟,筋材采用文献[9]给出的统一本构模型,这2种模型都能够同时较好地考虑材料的蠕变和动力滞回特性.分析采用ABAQUS软件.笔者编制了相应的程序添加到ABAQUS软件中,并应用上述筋土本构模型进行加筋土挡土墙静动力计算的合理性进行了验证[8].

假定填土为JTJ 015—91《公路加筋土工程设计规范》允许采用的低液限密实黏性土,地基为5m厚的砂土层,其下为基岩;筋材长度L=0.7H=5.6m,间距s=0.6m.筋材与土体的计算参数如下.

1.1 筋材

采用文献[9]所述高密度聚乙烯(HDPE)单向土工格栅,a=0.46×10-3(kN/m)-1,b=4.2×10-3(kN/m)-1,k1=1.1,k2=1.04,as=4.5×10-3(kN/m)-1,bs=7.0×10-3(kN/m)-1,η=2.0×109min,n0=2.6,c=10.0.其中:a,b为双曲线型、与时间无关的拉力-应变关系的2个参数;为双曲线型蠕变界线(static curve)的2个参数;k1,k2分别为土工合成材料卸载和反加载时初始刚度与单调加载时初始刚度的比值;η为黏滞系数;n0,c为材料常数.

1.2 砂土地基

采用文献[7-8]所述中密砂(相对密实度D r=0.62,内摩擦角 φ=37°),G0=1250,K0=1100,n G=n K=0.5,R′f=1.17,k1=1.8,k2=1.35,β=46.2°,d=0 kPa,ψ=0°,密度 ρ=1800 kg/m3.其中 :G0,nG为土体剪切模量常数;K0,nK为土体体积模量常数;k1,k2分别为土体卸载和反加载时初始剪切模量与单调加载时初始剪切模量的比值;R′f为材料常数;β,d分别为土体D-P屈服函数在p-q空间的倾角和截距;ψ为p-q空间下土体的剪胀角.

1.3 黏性土填土

采用文献[8]给出的计算参数(c=16 kPa,φ=30°),G0=550,K0=500,nG=nK=0.5,R′f=0.9,k1=1.65,k2=1.25,β=40.9°,d=24.0 kPa,ψ=0°,A=3.5×10-6s-1,ξ=0.11 kPa-1,m=0.85,t1=1 s,ρ=2000 kg/m3.其中:A,ξ,m,t1为土体Singh-Mitchell剪切蠕变模型的蠕变参数.

图2分别给出了上述填土在σ3=50 kPa围压(大致相当于填土的平均围压水平)时的剪切蠕变曲线和应力-应变曲线(假定经历2h从 σ1-σ3=0 kPa单调加载至 σ1-σ3=140kPa,其平均的应变加载速率约为 66×10-6/min;然后进行1Hz的快速循环加卸载).

有限元分析采用平面应变模型,并模拟了墙体的施工过程,筋材与面板、筋材与填土、填土与面板、填土与地基、面板与地基以及面板块与面板块之间均设置薄层接触单元.

以墙体经历5a静力蠕变时的受力和变形状态作为初始条件进行地震动力分析,基底输入选取了4种峰值均为0.4g的不同类型地震波,即Kobe波、El Centro波、Northridge波和兰州波(图3),动力计算过程采用ABAQUS/Standard所提供的隐式Hilber-Hughes-Taylor时域逐步积分法[10],有限元网格划分如图4所示.

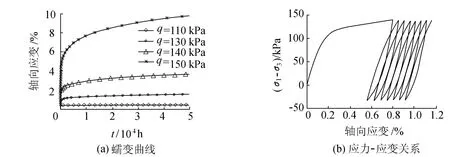
图2 填土的力学性质Fig.2 Mechanical properties of back-filled soils

图3 基底输入加速度Fig.3 Earthquake acceleration at the base

2 长期蠕变后墙体的地震动力响应

在研究不同地震类型的影响之前,本文以Kobe波为例先对加筋土挡土墙经历5a蠕变作用后的地震动力响应特性进行论述.

图4 有限元网格Fig.4 Finite element mesh

2.1 加速度反应

加筋区中部从基底至墙顶的加速度放大系数曲线如图5所示.在地基内部,加速度略有放大;在墙体中下部,放大系数较小,甚至小于1.0,说明此处土体出现了明显的屈服软化;在墙体上部,放大效应比较显著,且放大系数大体上沿高度呈线性增大,最大值出现在墙顶处.

2.2 墙面水平位移

图6为墙面底部、中部和顶部3点的水平总位移和动位移(等于总位移扣除蠕变5a的静位移)时程曲线.由图6可以看出,在震动初期,随着震动的加剧,墙面水平位移迅速增大,约15s之后逐渐趋于稳定,各点位移反应的最大值与残余值基本相同(故本文仅就位移残余值进行论述).

震后残余总位移和动位移沿墙高的分布曲线如图7所示.为了说明震前墙体蠕变的影响,图7还给出了墙体刚建成就遭遇Kobe波作用(此时则以墙体刚建成时的受力和变形状态作为动力分析的初始条件)的结果.由图7可以看出:(a)动位移和总位移大体上都随高度逐渐增大,最大值出现在墙顶附近,并且它们沿墙高的变化梯度是随着高度逐渐减小的;(b)震前经历蠕变时间长短即震前墙体蠕变变形大小对地震激励下墙体动位移(即震动引起的位移增量)的影响很小,但是由于材料明显的蠕变效应,墙体运行多年后再在地震作用下的总位移则会有较大增加.因此,一些规范中(如美国FHWA规范[11])在砂土填料基础上所做的设计假定“在满足规定的稳定性安全系数要求的情况下,墙体水平位移是在允许范围之内的”,对于震前经历长期蠕变作用的黏性土填料加筋土挡土墙而言缺乏一定的合理性.

图5 加筋区中部的加速度放大系数曲线Fig.5 Acceleration amp lification factor curve in m idd le of reinforced zone

图6 墙面水平位移时程曲线Fig.6 Time-history curve of lateral disp lacement on wall surface

2.3 筋材内力及墙体滑裂面

图8为墙体刚建成与经历5a蠕变2种情况之后地震作用下各层筋材的动拉力(指震动过程中每层筋材的拉力包络值,为与静拉力相区别,特称为动拉力)和动拉力增量(等于动拉力扣除震前该层筋材的静拉力)沿墙高的分布曲线.由图8可以看出:筋材动拉力和动拉力增量沿墙高都近似呈线性分布,最大值出现在下部的第1或第2层筋材上;震前经历蠕变时间长短对地震激励下筋材内力大小的影响不明显.

图7 墙面水平位移分布曲线Fig.7 Distribution curves of lateral displacement on wall surface

图8 筋材拉力沿墙高分布曲线Fig.8 Distribution curves of reinforcement tensile load along wall height

图9为墙体蠕变5a后在地震作用下各层筋材拉力(指筋材上每个点在震动过程中的最大拉力)沿筋长的分布.由于墙体中下部土体剪切作用明显,使得中下部几层筋材上各点(除第1层筋材)受力都比较大;对于中部几层筋材,拉力除了在筋材内部存在峰值点外,在筋材末端附近也存在峰值点,这意味着强震作用下墙体会同时存在内部和外部2个比较危险的滑裂面,而筋材最大内力及其位置分布则由这2个滑裂面一起决定.这一点也可从图10所给加筋区填土附近局部区域分别在震动开始时刻 t=0s(即5a静力蠕变过程的结束时刻)、基底加速度最大值时刻t=8.52s和震动结束时刻t=40s的八面体塑性应变等值线云图中得到更直观的证明:(a)内部滑裂面位于Rankine面附近,是由静力滑裂面在动力条件下继续发展而形成的;外部滑裂面开展得比较深,以较小倾角贯穿加筋区并向上延伸至墙顶,为双楔体或称组合破坏模式(two-part wedge failure或compound failure)的组合面形式(这与一些动力模型试验结果[12-14]相吻合).(b)随着震动时间的持续,内外部滑裂面都会逐渐发展,且在峰值0.4g的Kobe波强震作用下,外部面发展得更加明显;但其位置和形式基本不变.

图9 各层筋材拉力沿筋材长度分布Fig.9 Distribution of tensile load of each reinforcement layer along its length

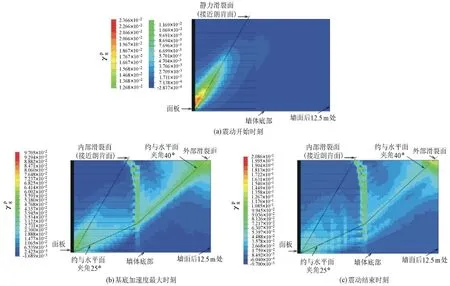
图10 等值线云图Fig.10 Contour of

3 不同输入地震波的影响

下面针对图3所示4种峰值相同的地震波对墙体蠕变5a后的地震动力响应进行影响分析.

3.1 加速度反应

从图11可以看出:不同地震波输入对墙体加速度放大效应的影响比较大.总体而言,兰州波和El Centro波的加速度响应相近,而Northridge波所引起的墙体加速度反应最显著.在这几种地震波作用下,加速度放大系数在地基以上墙体部分沿高度的变化范围都比较大,因此传统的拟静力设计法采用单一地震系数的做法对于高大挡土墙来说有欠合理性.

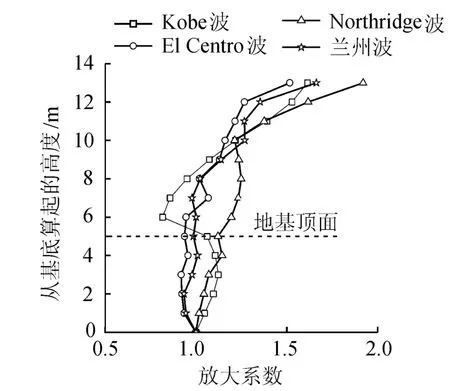
图11 加筋区中部的加速度放大系数曲线Fig.11 Acceleration am p lification factor curves in m iddle of reinforced zone

3.2 墙面水平位移

图12为震后残余水平总位移和动位移的分布曲线.不同地震波输入对墙体位移大小的影响比较明显,Northridge波作用下墙体位移最大,且比其他3种波大很多;Kobe波的作用次之,而兰州波和El Centro波的作用最弱,二者引起的墙体位移反应比较接近且其值都比较小.相对而言,El Centro波作用下墙体位移沿墙高的变化梯度要比兰州波稍大一些,这意味着El Centro波作用下填土的剪切变形比兰州波要更明显一些.

图12 墙面水平位移分布曲线Fig.12 Distribution curves of lateral disp lacement on wall surface

3.3 筋材内力及墙体滑裂面

各层筋材动拉力及动拉力增量沿墙高的分布曲线如图13所示.由图13可以看出:不同地震波输入对筋材内力大小的影响比较明显,对于受力较大的中下部筋材,Northridge波引起的内力最大,Kobe波次之,而兰州波和El Centro波的作用最弱,且二者引起的筋材内力反应比较接近.相对而言,由于El Centro波作用下填土剪切变形要比兰州波更明显一些,因而El Centro波所引起的筋材内力也会比兰州波稍大一些.

图13 筋材拉力沿墙高分布曲线Fig.13 Distribution curves of reinforcement tensile load along wall height

图14给出了各层筋材拉力沿筋材长度的分布,Kobe波、El Centro波、Northridge波和兰州波作用下加筋区填土附近局部区域在震动结束时刻的γp8等值线云图分别如图10和图15所示.由图10和图15可以看出:(a)在持时相对较短的兰州波作用下,外部滑裂面开展不明显,且靠近筋材的挡土区填土的塑性变形值较小,各层筋材最大拉力点的连线受内部滑裂面的影响最大,因而大体上接近Rankine面;而在其他3种地震波的作用下,因受外部滑裂面的影响相对比较明显,各层筋材最大拉力点的连线总体上向外偏离Rankine面.(b)在Kobe波、El Centro波、Northridge波和兰州波作用下,由经历5a蠕变作用的静力滑裂面在震动过程中继续开展而形成的内部滑裂面都位于Rankine面附近;在持时相对较短的兰州波作用下,整个震动过程外部滑裂面发展都不明显;在Kobe波和El Centro波作用下,外部滑裂面的位置和形式基本相同,都是大约从墙背底部以25°倾角向上延伸至筋材末端附近后再以40°倾角延伸至墙顶的组合面形式;Northridge波的作用最强,填土的塑性变形最显著,并且外部滑裂面相比Kobe波和El Centro波开展得更深一些,是一个大约从墙背底部以20°倾角向上延伸至筋材末端附近后再以35°～40°倾角延伸至墙顶的组合面形式.(c)总体而言,不同地震波类型虽然对滑裂面开展情况影响较明显,但是对滑裂面位置的影响不大.

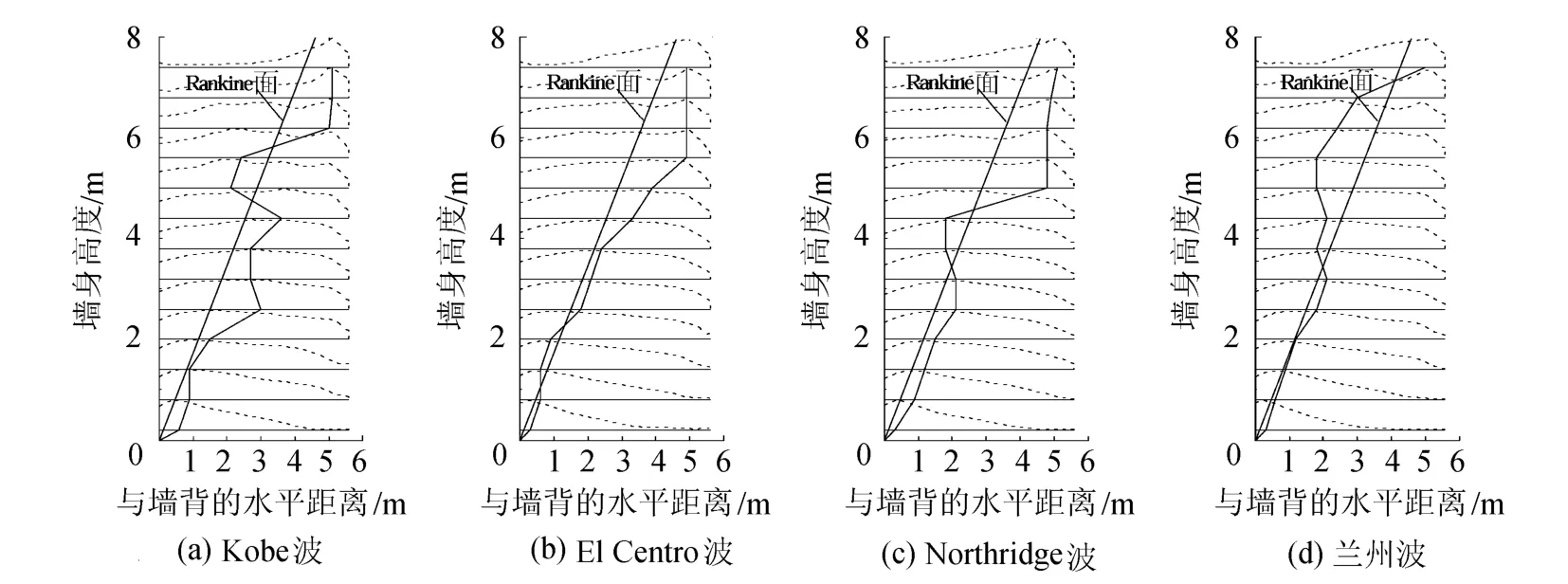
图14 各层筋材拉力沿筋材长度分布Fig.14 Tensile load distribution of each reinforcement layer along its length

图15 等值线云图Fig.15 Contour of

通过以上分析可知,尽管加速度峰值大小相同,但不同类型地震波所引起的墙体动力反应的差别可能会比较大.实际上,墙体的动力反应大小不仅与加速度峰值大小有关,还与地震波的持时、频谱特性以及墙体的基频等因素有关.一般的,地震波的加速度峰值越大、持时越长、卓越频率与墙体基频越接近,加筋土挡土墙的动力响应就会越明显.然而,目前许多相关规范却只应用加速度峰值进行抗震设计,而对其他几个影响因素的考虑不足,这种做法还有欠合理性.

4 结 论

a.强震作用下,加筋土挡土墙会同时存在内外部2个比较危险的滑裂面.内部滑裂面位于Rankine面附近,是由长期蠕变后的静力滑裂面在动力条件下继续发展而形成的;外部滑裂面通常为一以较小倾角贯穿加筋区并向上开展至墙顶的组合面.在不同地震波作用下,滑裂面的开展情况会有较大差别,但其位置变化不明显.

b.筋材、土体的明显蠕变效应会导致墙体运行多年再遭遇地震作用后,其总水平位移有较大增加.目前,一些规范(如FHWA规范)在蠕变效应不明显的砂土填料基础上所做的设计假定“在满足规定的稳定性安全系数要求的情况下,墙体水平位移是在允许范围之内的”,对于震前经历长期蠕变作用的黏性土填料加筋土挡土墙而言缺乏一定的合理性.当采用黏性土填料时,建议设计中对此予以充分考虑,或者适当限制黏粒含量并严格控制填土密实度,以减弱其蠕变效应.

c.地震波类型对墙体加速度放大效应影响比较明显.由于墙体比较高(8m),不同地震波作用下放大系数在墙体部分沿高度的变化范围都比较大,因此,传统的拟静力设计法采用单一地震系数的做法对于高大挡土墙来说欠合理.

d.加速度峰值相同的不同类型地震波所引起的墙体动力反应,如加速度、墙体水平位移和筋材内力等,差别可能会比较大,因此目前许多规范只应用加速度峰值进行加筋土挡土墙抗震设计的做法还有欠合理性,建议设计中还应该同时考虑地震波的持时与频谱特性(主要是地震波卓越频率与墙体基频的大小关系)等.

[1]MATSUO O,TSUTSUMI T,YOKOYAMA K,et al.Shaking table tests and analyses of geosynthetic-reinforced soil retaining walls[J].Geosythetics International,1998,5(1/2):97-126.

[2]LEE K Z,CHANG N Y,KO H Y.Numerical simulation of geosynthetic-reinforced soil walls under seismic shaking[J].Geotextiles and Geomenbranes,2010,28(4):317-334.

[3]LIU Hua-bei,WANG Xiang-yu,SONG Er-xiang.Long-term behavior of GRS retaining walls with marginal backfill soils[J].Geotextiles and Geomembranes,2009,27(4):295-307.

[4]王向余,刘华北,宋二祥.黏性土填土蠕变对土工合成材料加筋土挡土墙响应的影响[J].中国公路学报,2008,21(2):1-5.(WANG Xiang-yu,LIU Hua-bei,SONG Er-xiang.Influences of creep of cohesive back-filled soils on response of geosynthetic-reinforced soil retaining walls[J].China Journal of Highway and Transport,2008,21(2):1-5.(in Chinese))

[5]栾茂田,肖成志,杨庆,等.考虑蠕变性土工格栅加筋挡土墙应力与变形有限元分析[J].岩土力学,2006,27(6):857-863.(LUAN Mao-tian,XIAO Cheng-zhi,YANG Qing,et al.FEM based numerical analysis of stresses and deformations of geogrid-reinforced earth retaining walls[J].Rock and Soil Mechanics,2006,27(6):857-863.(in Chinese))

[6]LIU Hua-bei,WANG Xiang-yu,SONG Er-xiang.Reinforcement load and deformation mode of geosynthetic-reinforced soil walls subject to seismic loading during service life[J].Geotextiles and Geomembranes,2011,29(1):1-16.

[7]王向余,刘华北,宋二祥.一种实用的土体统一弹塑-黏塑性本构模型[J].河海大学学报:自然科学版,2009,37(2):166-170.(WANG Xiang-yu,LIU Hua-bei,SONG Er-xiang.A practical and unified elastoplastic-viscoplastic model of soil[J].Journal ofHohai University:Natural Sciences,2009,37(2):166-170.(in Chinese))

[8]王向余.长期蠕变后大型土工合成材料加筋土结构动力响应研究[D].北京:清华大学,2008.

[9]刘华北.土工合成材料循环受载、蠕变和应力松弛特性的统一本构模拟[J].岩土工程学报,2006,28(7):823-828.(LIU Huabei.Unified constitutive modeling of the cyclic,creep and stress relaxation behavior of geosynthetics[J].Chinese Journal of Geotechnical Engineering,2006,28(7):823-828.(in Chinese))

[10]Abaqus theory manual and analysis user's manual,version 6.5[EB].Providence,R.I.:ABAQUS Inc,2004.

[11]ELIAS V,CHRISTOPHER B R.Mechanically stabilized earth walls and reinforced soil slopes,design and construction guidelines[R].Report No.FHWA-SA-96-071.Washington,D.C.:FHWA,1996.

[12]TAKAHASH I A,TAKEMURA J,IZAWA J.Dynamic behavior of vertical geogrid-reinforced soil during earthquake[C]//YAGI N,JIANG Jing-cai.Proceedings of the International Symposium on Slope Stability Engineering.Rotterdam:A.A.Balkema Publishers,1999:991-996.

[13]TAKAHASH I A,TAKEMURA J,SH IMODAIRA T.Seismic performance of reinforced earth wall with geogrid[C]//Proc 15thICSMGE.Rotterdam:A.A.Balkema Publishers,2001:1265-1268.

[14]TATSUOKA F,KOSEKI J,TATEYAMA M,et al.Seismic stability against high seismic loads on geosynthetic-reinforced soil retaining structures[C]//ROWE R K.Proceedings of the 6thInternational Conference on Geosynthetics.Atlanta,Georgia:Industrial Fabrics Association International,1998:103-142.